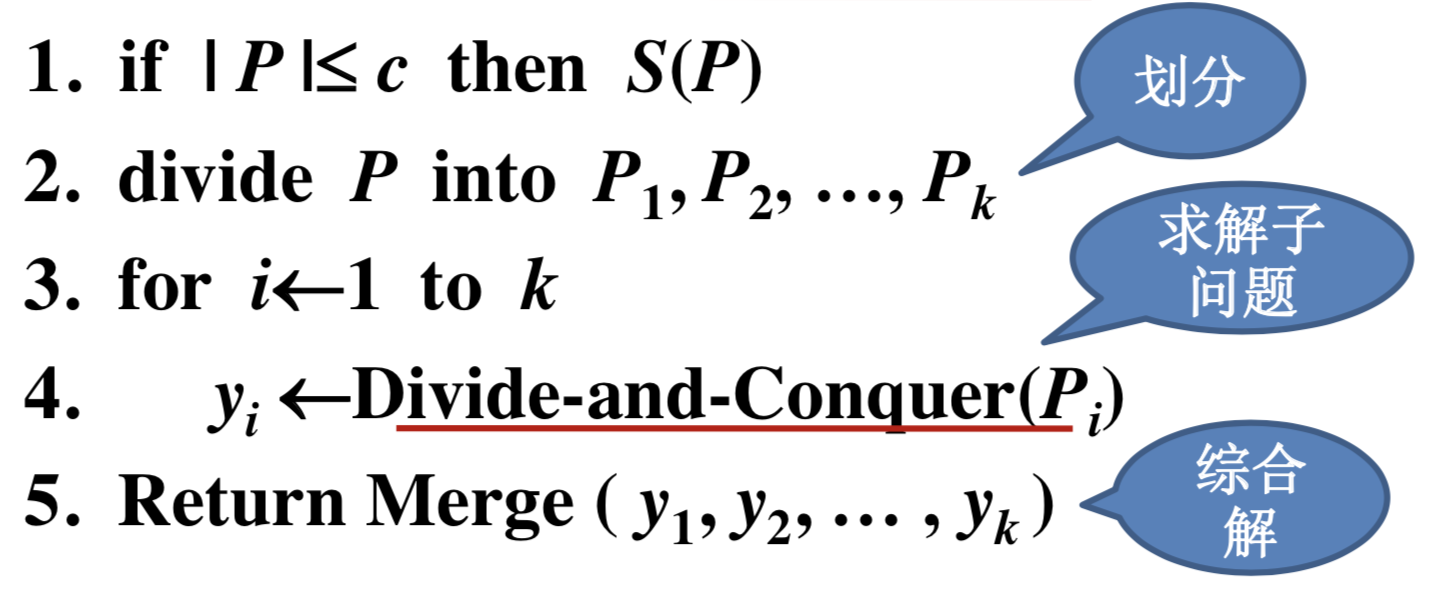【算法设计与分析】14 分治算法的一般描述和分析方法

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/qq_37375427/article/details/101618315

本文主要描述分治算法的一般描述和分析方法。衔接上一篇文章：【算法设计与分析】13 分治策略的设计思想

1 分治算法的一般性描述

• 设分治算法为：Divide-and-Conquer§

• 设计要点

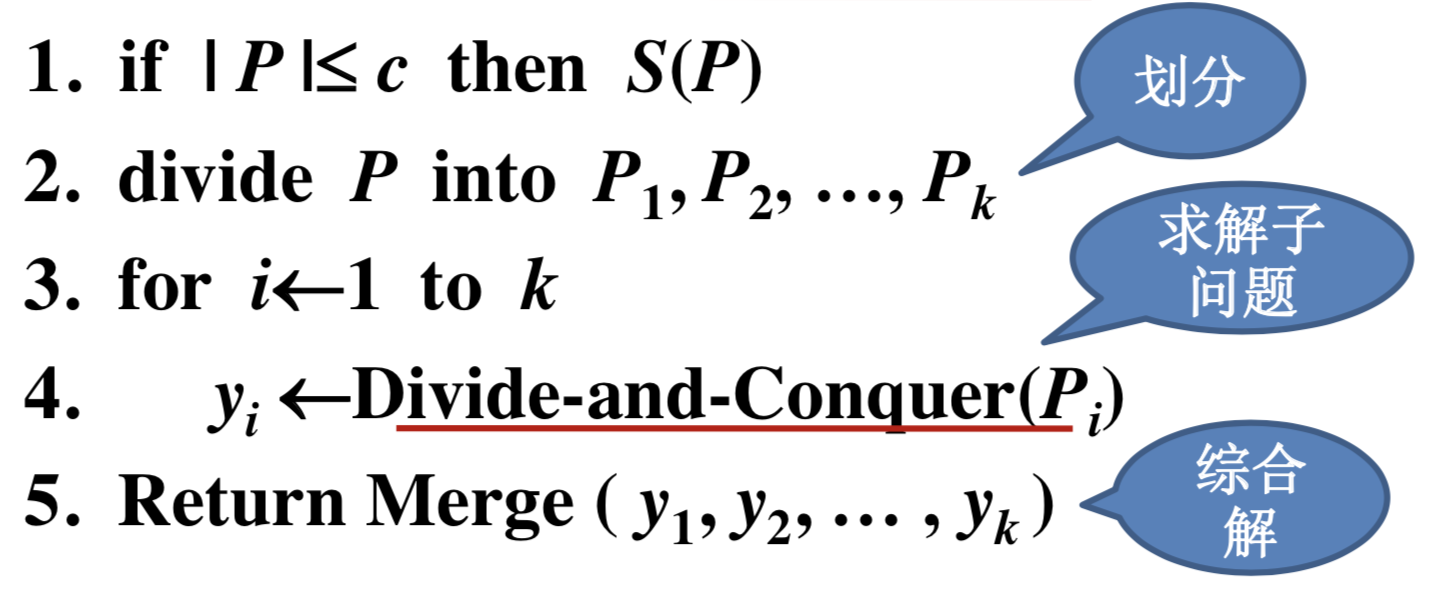
1. 原问题可以划分或者规约为规模较小的子问题。其中子问题之间遵循以下的规则：

    	1. 子问题与原问题具有相同的性质
    	2. 子问题的求解彼此独立
    	3. 划分时，子问题的规模尽可能均衡
   

2. 子问题较小时可以直接求解

3. 子问题的解综合可以得到原问题的解

4. 算法的实现：迭代或者递归

1.1 分支算法的时间分析

时间复杂度函数的递推方程：

• $W(n)=W(|P_1|)+W(|P_2|)+...+W(|P_k|)+f(n)$
• $W(c)=C$

其中

1. $P_1,P_2,...P_kw为划分后产生的子问题$
2. $f(n)为划分子问题以及将子问题的解综合得到原问题的解的总工足量$
3. 规模为c的最小子问题的工作两为：C

1.2 两类常见的递推方程与求解方法

• $f(n) = \sum_i^n a_i f(n-i)+g(n){， (1)}$
• $f(n)=af(\frac{n}{b}) + d(n){， (2)}$

例子：

Hanoi塔， $W(n)=2W(n-1)+1$
二分检索， $W(n)=W(n/2)+1$
归并排序， $W(n)=2W(n/2)+ n-1$

那么这些递推方程如何求解？

• 方程1： $f(n) = \sum_i^n a_i f(n-i)+g(n)$

1. 迭代法、递归树

• 方程2： $f(n)=af(\frac{n}{b}) + d(n)$

1. 迭代法、换元法、递归树、主定理

对于方程2，可以使用主定理，该定理可以很快求解出方程的解，前面的文章已经学习过主定理，这里再次提一下：

• 对于方程 $T(n)=aT(n/b)+d(n)$

1. 如果d(n)为常数：

$T(n)= \begin{cases} O(n^{log_ba}), & \text {$a \not= 1$} \\ O(logn), & \text{a=1} \end{cases}$

2. 如果d(n) = c(n)

$T(n)= \begin{cases} O(n), & \text {a < b} \\ O(nlogn), & \text{a=b} \\O(n^{log_b{a}}), &\text{a>b} \end{cases}$

注：上述的 $log_ba$中的b是以b为底的意思，但是上面的公式显示的不明显。

2 总结

• 想要彻底理解分治算法的思想，还需要多做练习，后面的文章会结合具体的例子，来讲解分治算法的思想在具体应用中的使用