版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
题意
求有多少 到 的排列,满足如下条件:
- 第 位是
- 以这个序列为入栈序列,可以只用一个栈,使用入栈出栈操作,使得出栈序列是升序。
思路
数数好题。
首先来发现性质:
- 对于序列里每一个数,都必须满足:他前面所有比他大的数组成的序列为降序。即不存在 满足 。而且只要满足性质1,就一定是合法序列。
- 对于任意一个子序列,找到其中的最大值,必须满足:最大值左边的数小于最大值右边的数。同样也是充分必要条件。
然后利用性质1来DP。(考试的时候我一直试图用第2个性质搞出点东西,但是失败告终。。。)
设 表示第 到 位已经填满,并且当前最小值是 的方案数。
当没有第 位填 的限制时,分类讨论第 位填的数:
- 第 位填 ,那么无论如何都可以满足性质1,所以
- 第 位填的数大于 ,那么为了满足性质1,第 位必须填大于 且没有填过的最小的那个数,否则这个未填过的最小数只能填在他的前面,那么这两个大于 的数就不满足降序了。所以
最终: 。
然后加上限制,显然当 的时候递推式不变。
当 时,分类讨论 的取值。
- 时,可以普通地DP,但是要去掉 。
- 时,发现 这些数必须选,并且必须放在 的位置上(反证法),但是位置无需固定。所以 (其中 是第 个卡特兰数,表示 的数的合法排列方案数)。
那么DP已经完成了。
然后可以把这个DP方程看成在一个二维的方阵里面走格点,如下图(题解里面贺的):
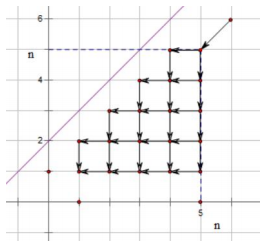
- 在第 列第 行
- 一个位置的DP值就是从右上角走到当前点的路径数
- 注意这条不能跨越的线比卡特兰数的那条往上挪了一格
- 注意上图是没有考虑 的限制的图,在有限制的图中,第 列上下之间没有连边
受卡特兰数的启发,我们可以用组合数快速地算出除了 这一列之外的某两个位置的之间的路径数。
那么我们只需要对于 这一列的每一个点,找到他从哪里更新过来,并且会对 有多少贡献就行了。
重点在DP,DP思路还是挺厉害的。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod = 1e9 + 7, N = 2e6 + 10;
int n, p, x;
int fc[N], ifc[N], ans;
template<class T>inline void read(T &x){
x = 0; bool fl = 0; char c = getchar();
while (!isdigit(c)){if (c == '-') fl = 1; c = getchar();}
while (isdigit(c)){x = (x<<3)+(x<<1)+c-'0'; c = getchar();}
if (fl) x = -x;
}
inline int fpow(int x, int y, int p){
int ret = 1;
while (y){
if (y & 1) ret = 1LL * ret * x % p;
x = 1LL * x * x % p;
y >>= 1;
}
return ret;
}
void init()
{
fc[0] = 1;
for (int i = 1; i <= n*2; ++ i)
fc[i] = 1LL * fc[i-1] * i % mod;
ifc[n*2] = fpow(fc[n*2], mod-2, mod);
for (int i = n*2-1; i >= 0; -- i)
ifc[i] = 1LL * ifc[i+1] * (i+1) % mod;
}
int C(int n, int m){
if (m > n || m < 0) return 0;
return 1LL * fc[n] * ifc[m] % mod * ifc[n-m] % mod;
}
int Cat(int n){
return (C(2*n, n) - C(2*n, n-1) + mod) % mod;
}
int F(int n, int m){
if (n > m) swap(n, m);
return (C(m+n, n) - C(m+n, n-2) + mod) % mod;
}
int main()
{
read(n); read(p); read(x);
init();
ans = 0;
for (int i = 1, ub = min(x, p); i <= ub; ++ i){
if (i == x){
(ans += 1LL * (F(p-1, i-1)-F(p-1, i-2)+mod) * (F(n-p, n-x)-F(n-(p+1), n-x)+mod) % mod) %= mod;
}
else if (i < x){
int nxti = p+x-i;
if (nxti <= n) (ans += 1LL * (F(p-1, i-1)-F(p-1, i-2)+mod) * (F(n-nxti, n-x)-F(n-(nxti+1), n-x)+mod) % mod * Cat(x-i) % mod) %= mod;
}
}
printf("%d\n", ans);
return 0;
}