组合数学是离散数学中的重要部分,早在17世幻就开始了这类课题的研究,当时是在赌博游戏的研究中出现了组合问题。
个体的计数可以求解许多问题,如确定算法的复杂度、分配能满足需求的电话号码,计算机系统中允许使用的密码…
计算原理
加法原理
如果完成第一项任务有 n 1 n_1 n1种方式,完成第二项任务有 n 2 n_2 n2种方式,并且这些任务不能同时完成,那么完成第一或第二项任务有 n 1 + n 2 n_1+n_2 n1+n2种方式。
例. 要选一位数学学院的教师或数学专业的学生作为校委会的代表。如果有37位教师和83位数学专业的学生,那么这个代表有多少种不同的选择?
答:完成第一项任务,选一位数学教师,可以有37种方式;完成第二项任务,选一位数学专业的学生,有83种方式,根据加法原理,结果有37+83=120种不同的选择。
乘法原理
假定一个过程被分解两个任务,如果完成第一个任务有 n 1 n_1 n1种方式,完成第二个任务有 n 2 n_2 n2种方式,那么完成这个过程有 n 1 ∗ n 2 n_1*n_2 n1∗n2种方式。
例1. 用一个字母和一个不超过100的正整数给礼堂的座位编号。那么不同的座位最多有多少?
答:给一个座位编号由两个任务组成,从26个字母中选择一个字母分配给它个座位,再从100个正整数中选择一个整数分配给它,可以有26*100=2600种方式。
例2. 如果每个车牌由3个字母后跟3个数字的序列构成,那么有多少个不同的有效的车牌。
答:共有 26 ∗ 26 ∗ 26 ∗ 10 ∗ 10 ∗ 10 = 17576000 26*26*26*10*10*10=17 576 000 26∗26∗26∗10∗10∗10=17576000种可能。
混合两种原理的计数问题
许多复杂的计数问题需要同时使用加法原理和乘法原理来求解。
例. 计算机系统的每个用户有一个6~8的字符构成的密码,其中每个字符是一个大写字母或数字,且每个密码至少包含一个数字,有多少可能的密码?
答:题目要求密码至少要包含一个数字,我们可以先算出所有可能的密码数,然后再减去不包含数字密码的数量,解答过程利用了容斥原理。
设 P P P是可能的密码总数, P 6 , P 7 , P 8 P_6,P_7,P_8 P6,P7,P8分别表过6位、7位、8位可能的密码数。
由乘法原理可得:
P 6 = 3 6 6 − 2 6 6 P_6=36^6-26^6 P6=366−266
P 7 = 3 6 7 − 2 6 7 P_7=36^7-26^7 P7=367−267
P 8 = 3 6 8 − 2 6 8 P_8=36^8-26^8 P8=368−268
再由加法原理可得: P = P 6 + P 7 + P 8 P=P_6+P_7+P_8 P=P6+P7+P8
容斥原理
为了正确地计数完成其中一个任务的数量,我们先把完成每个任务的方式数量加起来,然后再减去同时完成两个任务的方式数,这就是容斥原理。
例1. 以1开始或者以00结束的8位二进制符号串有多少个?
设: A = { 以 1 开 始 的 8 位 二 进 制 位 } A=\{以1开始的8位二进制位\} A={
以1开始的8位二进制位}
B = { 以 00 结 束 的 8 位 二 进 制 位 } B=\{以00结束的8位二进制位\} B={
以00结束的8位二进制位}
C = { 答 案 } C=\{答案\} C={
答案}
C = ∣ A ∪ B ∣ − ∣ A ∩ B ∣ C=|A∪B|-|A∩B| C=∣A∪B∣−∣A∩B∣
A = 2 7 , B = 2 6 , A ∩ B = 2 5 A=2^7 ,B=2^6, A∩B=2^5 A=27,B=26,A∩B=25
C = 128 + 64 − 32 = 160 C=128+64-32=160 C=128+64−32=160
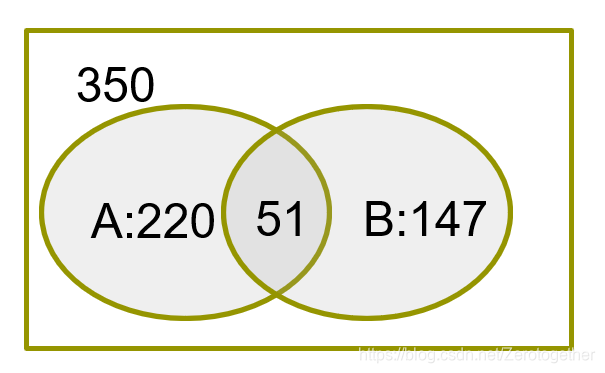
例2.某计算机公司收到了350份计算机毕业生的工作申请书。假如这些申请人中有220人主修的是计算机科学专业,有147人主修的是商务专业,有51人即主修了计算机科学专业又主修了商务专业,那么,有多少个申请人既没有主修计算机科学专业又没有主修商务专业?
根据容斥原理,主修计算机或主修商务专业的学生人数为: ∣ A U B ∣ = ∣ A ∣ + ∣ B ∣ − ∣ A ∩ B ∣ = 220 + 147 − 51 |AUB|=|A|+|B|-|A∩B| =220+147-51 ∣AUB∣=∣A∣+∣B∣−∣A∩B∣=220+147−51
又根据容斥原理,既没有主修计算机又没有主修商务专业的人数为: 350 − 316 = 34 350-316=34 350−316=34
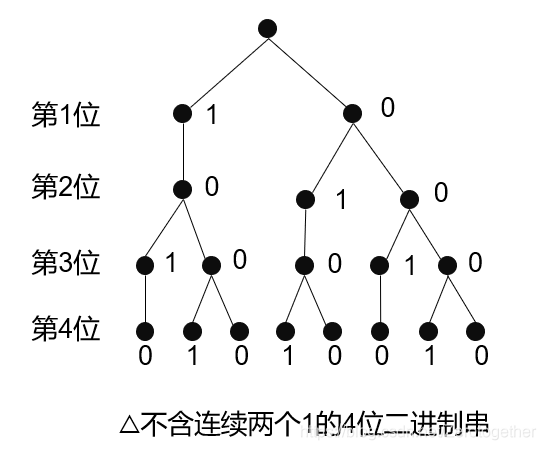
树图
我们可以在某些计数问题中使用数,树的每个分支表示每个可能的选择,用树叶表示可能的结果。
例. 有多少个不含连续两个1的4位二进制串?
排列和组合
许多计数类问题可以通过找到特定大小的集合中不同元素排列的不同方法数来得以解决,其中这些次序是有限制的。有些问题是通过从特定大小的集合元素中选择数量的方法数,这些元素的次序是不受限制的。
排列
从 n n n个不同元素中,任取 m m m个元素,按照一定的顺序排成一列,叫做从 n n n个不同元素中取出 m m m个元素的一个排列.
记作: A n m = n ( n − 1 ) ( n − 2 ) . . . ( n − m + 1 ) = n ! ( n − m ) ! A_n^m=n(n-1)(n-2)...(n-m+1)=\frac{n!}{(n-m)!} Anm=n(n−1)(n−2)...(n−m+1)=(n−m)!n!
也可以记作: P ( n , m ) = n ( n − 1 ) ( n − 2 ) . . . ( n − m + 1 ) . P(n,m)=n(n-1)(n-2)...(n-m+1). P(n,m)=n(n−1)(n−2)...(n−m+1).
例1. 在进入竞赛的100个不同的人中有多少种方法选出一个一等奖得主、一个二等奖得主和一个三等奖得主?
答:从100个元素中有序选择3个元素的方法数,即100个元素的集合的3排列数。
因此,答案是:
P ( 100 , 3 ) = 100 ∗ 99 ∗ 98 = 970200 P(100,3)=100*99*98=970 200 P(100,3)=100∗99∗98=970200
例2. 字母ABCDEFGH有多少种排列包含串ABC?
解:由于字母ABC必须成组出现,我们通过找6个对象,即组ABC和其它的5个字母进行排列得到答案,答案为 6 ! = 720 6!=720 6!=720 种方式。
组合
从 n n n个不同元素中,任取 m m m个元素,并成一组,叫做从 n n n个不同元素中取出 m m m个元素的一个组合.
组合跟元素的顺序无关。
C n m = A n m A m m = n ( n − 1 ) ( n − 2 ) . . . ( n − m + 1 ) m ! = n ! m ! ⋅ ( m − m ) ! C_n^m=\frac{A_n^m}{A_m^m}=\frac{n(n-1)(n-2)...(n-m+1)}{m!}=\frac{n!}{m!\cdot(m-m)!} Cnm=AmmAnm=m!n(n−1)(n−2)...(n−m+1)=m!⋅(m−m)!n!
证明:
∵ A n m = C n m ⋅ A m m \because A_n^m=C_n^m\cdot A_m^m ∵Anm=Cnm⋅Amm, ∴ C n m = A n m A m m \therefore C_n^m=\frac{A_n^m}{A_m^m} ∴Cnm=AmmAnm
例. A 4 3 = C 4 3 ⋅ A 3 3 A_4^3=C_4^3\cdot A_3^3 A43=C43⋅A33, C 4 3 = = A 4 3 A 3 3 C_4^3==\frac{A_4^3}{A_3^3} C43==A33A43
组合数恒等式: C n m = C n n − m C_n^m=C_n^{n-m} Cnm=Cnn−m,如 C 7 2 = C 7 5 . C_7^2=C_7^5. C72=C75.
证明 设 S S S是 n n n个元素的集合。 S S S的每个具有 r r r个元素的子集 A A A对应一个具有 n − r n-r n−r个元素的子集 A ‾ \overline A A.
例1. 从一幅52张标准扑克牌中选出5张,共有多少种不同的方法?从一副52张扑克牌中选出47张,又有多少种不同的方法?
问题1: A n s = C ( 52 , 5 ) Ans=C(52,5) Ans=C(52,5)
问题2: A n s = C ( 52 , 47 ) Ans=C(52,47) Ans=C(52,47)
例2. 为开发学校的离散数学课程要选出一个委员会,如果数学系有9个教师,计算机科学系有11个教师。而这个委员会由3个数学系的教师和4个计算机科学系的教师组成,那么有多少种选择方式?
A n s = C ( 9 , 3 ) ∗ C ( 11 , 4 ) = 84 ∗ 330 = 27720 Ans=C(9,3)*C(11,4)=84*330=27 720 Ans=C(9,3)∗C(11,4)=84∗330=27720
有重复的排列
定理: 具有 n n n个物体的集合允许重复的 r r r排列数是 n r n^r nr.
例. 用英文字母可以构成多少个 r r r位字符串?
答:存在 2 6 r 26^r 26r个 r r r位字符串。
有重复的组合
定理: n n n个元素的集合中允许重复的 r r r组合有 C n + r − 1 r = C n + r − 1 n − 1 C_{n+r-1}^r=C_{n+r-1}^{n-1} Cn+r−1r=Cn+r−1n−1个。
例. 从包含1美元、2美元、5美元、10美元、20美元、50美元及100美元的钱袋中选5张纸币,有多少种方式?假定不管纸币被选的次序,同种币值的纸币是不加区别的,并且至少每种纸币有5张。
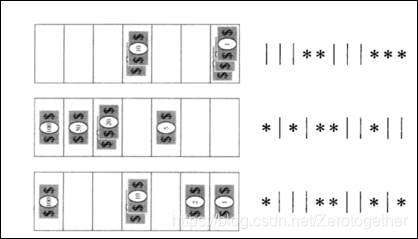
答:题目要求从7个元素集合中取允许重复的5的组合数,我们可以想象在7个盒子中放入5张纸币,
选择5张纸币的方法数对应了6条竖线和5颗星的方法数,因此,选择5张纸币的方法数就是从11个位置选5颗星位置的方法数,这对应从含11个元素的集合中无序地选择5个元素的方法数,总共有C(11,5)种方式。具体如图所示。
具有不可区物体的集合的排列
例.重新排序单词SUCCESS中的字母能多少个不同的串?
答:这个单词某些字母是重复的,答案并不是7个字母的排列数。
这个单词包含了3个S,2个C,1个U,和1个E。
3个S可以用 C 7 3 C_7^3 C73种不同的方式放在7个位置中;2个C用 C 4 2 C_4^2 C42 种方式放入剩下的4个空位中;1个U用 C 2 1 C_2^1 C21种方式放到剩下的2个空位中;还剩1个E,有 C 1 C_1 C1种方式放下最后一个空位中。
A n s w e r = C 7 3 ⋅ C 4 2 ⋅ C 2 1 ⋅ C 1 1 = 420. Answer=C_7^3\cdot C_4^2 \cdot C_2^1 \cdot C_1^1=420. Answer=C73⋅C42⋅C21⋅C11=420.
将物体放入盒子中
可辨别的物体和可辨别的盒子
例. 有多少种把52张扑克牌发给4个人使得每个人5张牌?
答:使用乘法原理,第一个1得到5张牌有 C 52 5 C_{52}^5 C525种方式,第二个人有 C 47 5 C_{47}^5 C475 种方式…第四个人可以有 C 37 5 C_{37}^5 C375 种方式,因此发给4个人每人5张牌的方式总数是: C 52 5 ⋅ C 47 5 ⋅ C 42 5 ⋅ C 37 5 C_{52}^5\cdot C_{47}^5 \cdot C_{42}^5 \cdot C_{37}^5 C525⋅C475⋅C425⋅C375
不可辨别的物体与可辨别的盒子
例. 将10个不可辨别的球放入8个可辨别的桶里,共有多少种不同的方法?
答:将10个不可辨别的球放入8个可辨别的桶里的方法数等于在允许重复计数的情冲下,从8个元素的集合中取出10组合的个数,即有重复的组合,因此有 C 8 + 10 − 1 10 = C 17 10 = 19448 C_{8+10-1}^{10}=C_{17}^{10}=19 448 C8+10−110=C1710=19448
可辨别的物体与不可辨别的盒子
例. 将4个不同的雇员安排在3间不可辨别的办公室,有多少种方式?其中每间办公室可以安排任意个数的雇员。
解:集合的划分,设S(4,n)(1<=n<=4)为将4个雇员放入到n个办公室(划分成n个集合)
根据加法原理:
Ans=S(4,3)+S(4,2)+S(4,1)=6+7+1=14种。
上述所说的问题称为第二类Stirling数,定义如下:将 n n n个有区别的物体放入 m m m个相同的盒子里,且没有空盒子。
设 S ( n , m ) S(n,m) S(n,m)为将 n n n个有区别的物体放入 m m m个相同的盒子里且没有空盒的方案数量;
{ S ( n , 0 ) = 0 , ( m = 0 ) S ( n , 1 ) = 1 , ( m = 1 ) S ( n , n ) = 1 S ( n , k ) = 0 , ( k > n ) S ( n , m ) = m ⋅ S ( n − 1 , m ) + S ( n − 1 , m − 1 ) , ( 1 < m < n ) \begin{cases} S(n,0)=0,\ (m=0) \ \\S(n,1)=1,\ (m=1) \\S(n,n)=1 \\S(n,k)=0 ,(k>n) \\S(n,m)=m\cdot S(n-1,m)+S(n-1,m-1) ,\ \ (1<m<n) \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧S(n,0)=0, (m=0) S(n,1)=1, (m=1)S(n,n)=1S(n,k)=0,(k>n)S(n,m)=m⋅S(n−1,m)+S(n−1,m−1), (1<m<n)
上面的递归公式的第1行至第4行在编写程序时可作为边界条件进行初始化;
简单说一下第5行的公式 S ( n , m ) = m ⋅ S ( n − 1 , m ) + S ( n − 1 , m − 1 ) S(n,m)=m\cdot S(n-1,m)+S(n-1,m-1) S(n,m)=m⋅S(n−1,m)+S(n−1,m−1)的证明过程:
假定 n n n个元素的集合中包含某个元素 a a a,那么 S ( n , m ) S(n,m) S(n,m)这个问题的求解可划分为两个子问题:
子问题1:某个盒子只放元素 a a a的划分方案,递归地求解 S ( n − 1 , m − 1 ) S(n-1,m-1) S(n−1,m−1)即可。(放在哪个盒子里都一样,盒子不可区分)
子问题2:某个盒子不仅仅只放元素 a a a的划分方案,单独把 a a a元素拿出来,先求解出 n − 1 n-1 n−1个元素放到m个盒子的方案数,即递归地求解 S ( n − 1 , m ) S(n-1,m) S(n−1,m)的解,因为元素 a a a和其它元素都是可区分的,元素 a a a可以放到 S ( n − 1 , m ) S(n-1,m) S(n−1,m)划分好的任意一个盒子内,根据加法原理,总共有m种放法,即 m ⋅ S ( n − 1 , m ) m\cdot S(n-1,m) m⋅S(n−1,m)。
不可辨别的物品和不可辨别的盒子
例-放苹果
将 n n n个同样的苹果和 m m m个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?
答:
设 f ( n , m ) f(n,m) f(n,m)为放 n n n个不可辨别的物品放入到 m m m个不可辨别的盒子里的方案数量。
f ( n , m ) = { 1 , ( n = 1 o r n = 0 ) 1 , ( m = 1 ) f ( n , n ) , ( m > n ) f ( n , m − 1 ) + f ( n − m , m ) , ( m < = n ) f(n,m)=\begin{cases} 1 ,\ (n=1 \ or \ n=0) \\1,\ (m=1) \\ f(n,n),\ (m>n) \\ f(n,m-1)+f(n-m,m)\ \ ,\ (m<=n)\end{cases} f(n,m)=⎩⎪⎪⎪⎨⎪⎪⎪⎧1, (n=1 or n=0)1, (m=1)f(n,n), (m>n)f(n,m−1)+f(n−m,m) , (m<=n)
关于第4行公式 f ( n , m ) = f ( n , m − 1 ) + f ( n − m , m ) f(n,m)=f(n,m-1)+f(n-m,m) f(n,m)=f(n,m−1)+f(n−m,m)的解释,同样地,把 f ( n , m ) f(n,m) f(n,m)拆分成两个子问题:
子问题1:允许至少有一个盘子是空着,递归地求解 f ( n , m − 1 ) f(n,m-1) f(n,m−1)的值;
子问题2:不允许有盘子是空着,意味着每个盘子都至少放一个苹果,即 m m m个盘子放 m m m个苹果,还剩下 n − m n-m n−m个苹果,递归地求解 f ( n − m , m ) f(n-m,m) f(n−m,m)的值即可;
所以 f ( n , m ) = f ( n , m − 1 ) + f ( n − m , m ) . f(n,m)=f(n,m-1)+f(n-m,m). f(n,m)=f(n,m−1)+f(n−m,m).
将 n n n个不可辨别的物体放入 k k k个不可辨别的盒子,等价于将正整数 n n n划分成 j j j个正整数相加的方案数。
生成排列和组合
前面我们已经学习了各种类型的排列和组合的计数方法, 但是有时候需要生成排列和组合,而不仅仅是计数。
第一,假设一个销售商必须访问6个城市。应该按照什么顺序访问这些城市而使得总的旅行时间最少?一种方法就是确定6!=720种不同顺序的访问时间并且选择具有最小旅行时间的访问顺序。
第二,假定6个数的集合中某些数的和是100.找出这些数的一种方法就是生成所有26=64个子集并且检查它们的元素和。
生成排列
生成 n n n个最小正整数的排列,排列集合的顺序以字典顺序为基础的,对于某个 k , 1 ≤ k ≤ n , a 1 = b 1 , a 2 = b 2 , . . . , a k − 1 = b k − 1 k,1≤k≤n,a_1=b_1,a_2=b_2,...,a_{k-1}=b_{k-1} k,1≤k≤n,a1=b1,a2=b2,...,ak−1=bk−1并且 a k < b k a_k<b_k ak<bk,那么排列 a 1 a 2 . . . a n a_1a_2...a_n a1a2...an在排列 b 1 b 2 . . . b k b_1b_2...b_k b1b2...bk的前边。
例.集合 1 , 2 , 3 , 4 , 5 {1,2,3,4,5} 1,2,3,4,5的排列 23415 23415 23415在排列 23514 23514 23514的前边,因为这些排列在在前两位相同,但第一排列在第三位置中的数是 4 4 4,小于第二个排列在第三位置中的数 5 5 5。类似地,排列 41532 41532 41532在排列 52143 52143 52143的前边。
如何根据给定的排列生成下一个排列?
对于给定的排列 a 1 a 2 . . . a n a_1a_2...a_n a1a2...an,首先找到整数 a j a_j aj和 a j + 1 a_{j+1} aj+1使得 a j < a j + 1 a_j<a_{j+1} aj<aj+1且 a j + 1 > a j + 2 > . . . > a n . a_{j+1}>a{j+2}>...>a_n. aj+1>aj+2>...>an.
把 a j + 1 , a j + 2 , . . . a n a_{j+1},a_{j+2},...a_n aj+1,aj+2,...an中大于 a j a_j aj的最小的整数放到第 j j j个位置,再按照递增顺序重新填充其余的整数。
例. 在362541后面按字典序的下个一最大的排列是什么?
答:找到使得 a j < a j + 1 a_j<a{j+1} aj<aj+1的一对整数: a 3 = 2 , a 4 = 5 a_3=2,a_4=5 a3=2,a4=5,在541中找出一个数 4 大于 a 3 a_3 a3的值并填入 a 3 a_3 a3的位置,{2,5,1}再按照递增的顺序填入 a 4 a_4 a4到 a 6 a_6 a6的位置中,排列为364125。
实现代码:
//算法过程:根据当前的序列求出下一个排列的序列,递归地调用整个过程
#include <iostream>
#include <algorithm>
using namespace std;
void permutation(int a[],int n,int rr){
for(int i=1;i<=rr;i++)
cout<<a[i]<<' ';
cout<<endl;
//从右往左(从低位到高位),找到下标a_j<a_j+1
int j=n-1;
while(a[j]>a[j+1]&&j>0) j--;
//判断当前是否是最后一个序列,是则跳出递归调用
if(j==0) return ;
//ak是在aj右边大于aj的最小整数
int k=n;
while(a[j]>a[k]) k--;
//交换ak和aj
swap(a[j],a[k]);
int r=n;
int s=j+1;
while(r>s){
swap(a[r],a[s]);
r--;
s++;
}
//sort(a+j+1,a+n+1);
permutation(a,n,rr);
}
int main(){
int a[]={
0,1,2,3,4,5,6,7,8,9};
permutation(a,9,9);
return 0;
}
算法思路:
1.找到 a j a_j aj的位置使得 a j < a j + 1 a_j<a{j+1} aj<aj+1;
2.在 a j + 1 a_{j+1} aj+1到 a n a_n an中找出一个数 a k a_k ak的值使得 a k > a j a_k>a_j ak>aj.
3.对 a j + 1 a_{j+1} aj+1到 a n a_n an范围的值进行从小到大排序,又因为 a j + 1 a_{j+1} aj+1到 a n a_n an的值本来是已经是一个从大到小排好序的序列,从降序的序列变为升序的序列,只需依次交换前后两个位置的值即可。
除了用上述的算法过程外,我们还可以使用C++中的STL来生成下一个序列。
//代码来源:算法竞赛入门经典 第二版
#include<cstdio>
#include<algorithm> //包含next_permutation
using namespace std;
int main( ) {
int n, p[10];
scanf("%d", &n);
for(int i = 0; i < n; i++)
scanf("%d", &p[i]);
sort(p, p+n); //排序,得到p的最小排列
do {
for(int i = 0; i < n; i++) printf("%d ", p[i]); //输出排列p
printf("\n");
}
while(next_permutation(p, p+n)); //求下一个排列
return 0;
}
更多的使用方法,可查看链接:生成下一个排列使用方法
康托展开
具体内容请查看链接:康托展开
生成组合
怎样可以生成一个有穷集的元素的所有组合呢?
由于一个组合就是生成的一个子集,我们可以利用在 { a 1 , a 2 , … a n } \{a1 , a2,…an\} {
a1,a2,…an}和 n n n位二进制位之间的对应.
如果元素 a k a_k ak在子集中,对应的二迸制串在位置 k k k为1,如果 a k a_k ak不在子集中,对应的二进制串在位置 k k k为0.
如果可以列出所有的n位二进制串,那么通过在子集和二进制串之间的对应就可以列出所有的子集。
如何通过当前的二进制串找到下一个二进制串?
假设有 n n n个元素,它的二进制串是一个0到 2 n − 1 2^{n-1} 2n−1之间的二进制展开式,首先确定从右边起第一个不是1的位置 a k a_k ak,把 a k a_k ak的0变成1,再把 a k + 1 a_{k+1} ak+1到 a n a_n an的二进制数全变为0.
例. 找出在100010 0111后面的下一个二进位串.
答 这个串从右边数不是1的第1位是从右边起的第4位。把这一位变成1并且将它后面所有的位变成0.这就生成了下一个最大的二进位为100010 1000.
二项式系数
二项式定理:
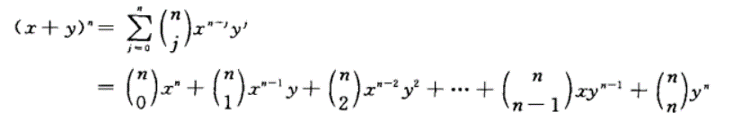
以求 ( x + y ) 3 (x+y)^3 (x+y)3为例.
( x + y ) 3 = ( x + y ) ( x + y ) ( x + y ) (x+y)^3=(x+y)(x+y)(x+y) (x+y)3=(x+y)(x+y)(x+y),求项 x 3 , x 2 y , x y 2 , y 3 x^3,x^2y,xy^2,y^3 x3,x2y,xy2,y3的系数。
以求 x y 2 xy^2 xy2的系数为例,取两个 y y y相乘得到 y 2 y^2 y2,再同另一个 x x x相乘得到 x y 2 xy^2 xy2,总共有 C 3 2 = 3 C_3^2=3 C32=3种不同的方式。下图显示了如何取得 x y 2 xy^2 xy2的过程,也就是从3个 y y y中取2个 y y y的组合数。

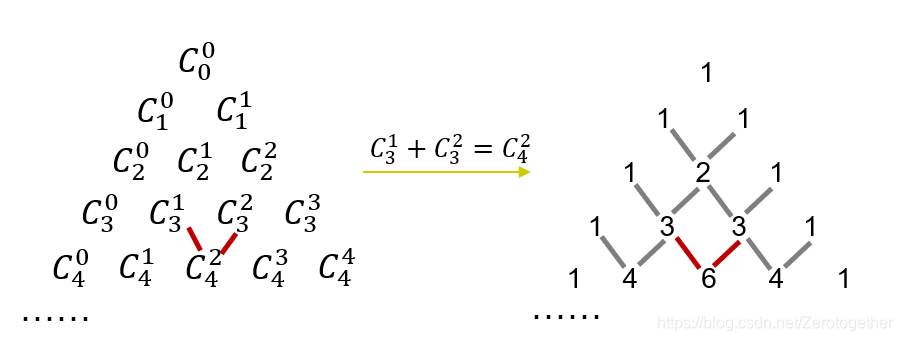
杨辉三角
帕斯卡恒等式也称为杨辉三角,帕斯卡恒等式的定义如下:
设 n n n和 k k k是满足 n ≥ k n\geq k n≥k的正整数,那么有: C n + 1 k = C n k − 1 + C n k . C_{n+1}^k=C_n^{k-1}+C_n^k. Cn+1k=Cnk−1+Cnk.
证明 假设 T T T是包含 n + 1 n+1 n+1个元素的集合,令 a a a是 T T T的一个元素且 S = T − { a } S=T-\{a\} S=T−{ a}, T T T包含 k k k个元素的子集有 C n + 1 k C_{n+1}^k Cn+1k个。
将“ T T T包含 k k k个元素的子集个数”拆分成两个包含 a a a和不包含 a a a的子问题。
情况1: 划分的子集包含 a a a,问题变成了“求集合 S S S包含 k − 1 k-1 k−1个元素的子集个数”,有 C n k − 1 C_{n}^{k-1} Cnk−1个,因为包含元素 a a a,所以是 k − 1 k-1 k−1,元素 a a a可以放到 C n k − 1 C_{n}^{k-1} Cnk−1个划分中的任意一个划分。
情况2: 划分的子集不包含 a a a,问题就变成了“求集合 S S S划分 k k k个元素的子集个数”,答案为 C n k C_n^k Cnk
通过初始化 C n 0 = C r r = 1 , ( 0 ≤ r ≤ n ) C_n^0=C_r^r=1,\ (0\leq r\leq n) Cn0=Crr=1, (0≤r≤n),使用帕斯卡恒等式通过递推运算,可以算出所有的组合数 C n r , ( 0 ≤ r ≤ n ) C_n^r\ ,(0\leq r\leq n) Cnr ,(0≤r≤n)。具体如下图所示。
卡特兰数
卡特兰数的相关案例和应用很多,比如说二叉树的计数、括号匹配、出栈序列和正多边形的三角剖分,下面我们以书本上的二叉树的计数和正多边形的三角剖分为例讲解。
例1.树的计数
问题:具有 n n n个结点的不同形态的二叉树有多少棵?
下图给出了当 n = 2 , n = 3 , n n=2,n=3,n n=2,n=3,n的一般情形的情况。
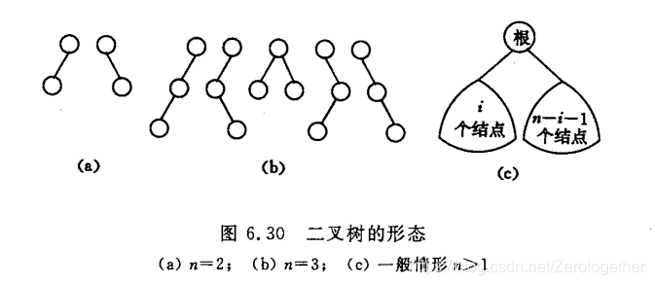
设 C n C_n Cn为 n n n个,根据左右孩子结点数的讨论,可以递归地定义为:
C n = C 0 C n − 1 + C 1 C n − 2 + + C 2 C n − 3 + . . . + C n − 2 C 1 + C n − 1 C 0 . 0 C_n=C_0C_{n-1}+C_1C_{n-2}++C_2C_{n-3}+...+C_{n-2}C_1+C_{n-1}C_0.0 Cn=C0Cn−1+C1Cn−2++C2Cn−3+...+Cn−2C1+Cn−1C0.0
需要注意的是,根节点占用了一个节点,所以左右孩子 的节点数量相加为 n − 1 n-1 n−1。
当 n = 6 n=6 n=6时, C 6 = C 0 C 5 + C 1 C 4 + C 3 C 2 + C 2 C 3 + C 4 C 1 + C 5 C 0 C_6=C_0C_5+C_1C_4+C_3C_2+C_2C_3+C_4C_1+C_5C_0 C6=C0C5+C1C4+C3C2+C2C3+C4C1+C5C0
因为上述的公式中有很多重复求解的子问题,在编写程序递归求解时,可以使用记忆化搜索优化。
当然,也可以直接使用公式求解:
含有 n n n个结点且不相似的二叉树有 C 2 n n ⋅ 1 n + 1 C_{2n}^n \cdot \frac{1}{n+1} C2nn⋅n+11 棵。
这就是著名的卡特兰数(Catalan number)。
注:编写程序求解组合数建议使用上述的杨辉三角来求解。
补充说明: 在初赛时,如果记不住卡特兰数公式,或者解题的公式有递归调用关系的,可以手动模拟递归求解的过程,先求解(枚举)出某个小的子问题的解,再根据公式求出更大的子问题的解,最后根据依赖关系求出最终解。
例2.正多边形的三角剖分
问题:在一个凸n边形中,通过不相交于n边形内部的对象线,把n边形拆分成若干个三角形。例如五边形有如下五种拆分的方案。

思路:
一个正N边形可以将其拆分成三个部分,固定某一条边(P1,Pn),和剩于的点组成一个三角形,①部分组成的三角形,及②、③部分组成的多边形。原多边形被拆分为两个子问题②和③。
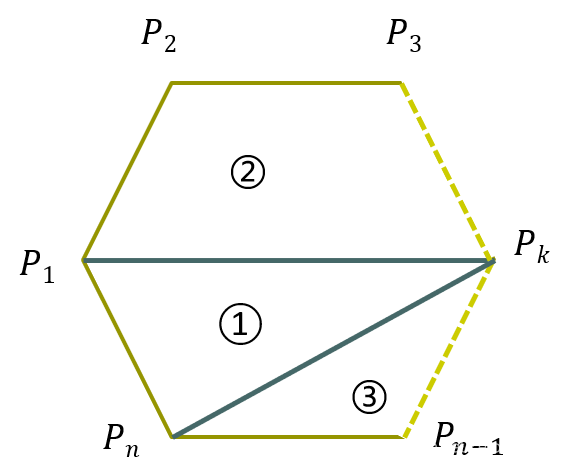
将①看成是根节点, ②和③看成树的计数中的左右孩子结点,思路和树的计数是一样的!
更多关于卡特兰数的内容,请查看下面的链接:
1.https://zhuanlan.zhihu.com/p/31317307
2.https://zhuanlan.zhihu.com/p/31526354 (里面有卡特兰数的计算过程)
参考资料来源:《离散数学及其应用 本科教学版 原书第6版》