算法分析与设计——NP

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接： https://blog.csdn.net/qq_40438165/article/details/102552430

一、多项式规约

1、概念及性质

$\quad$多项式时间归约：如果问题X和问题Y满足以下两条性质，那么问题X可以在多项式时间归约到问题Y。

• 问题X可以通过多项式时间的基本运算步骤转换为问题Y；
• 问题X多项式次调用求解问题Y的算法
  记为 $X\le_{P}Y$。三点性质：
• 若 $X\le_{P}Y$， $Y$能在多项式时间内求解，则 $X$也能在多项式时间内求解
• 若 $X\le_{P}Y$， $X$不能在多项式时间内求解，则 $Y$也不能在多项式内求解
• 若 $X\le_{P}Y$且 $Y\le_{P}X$，则 $X,Y$多项式等价，记为 $X ≡_{P} Y$。 $X,Y$中一方能在多项式时间内求解则另一方也能在多项式时间内求解。

2、点独立集和点覆盖

$\quad$点独立集：在图 $G$中选出若干个顶点，这些顶点之间没有边相连接，称为点独立集。一个图中所有点独立集中点数最多的集合称为图的最大点独立集。
$\quad$点覆盖：在图 $G$中选出若干个顶点组成集合 $S$，使得图中每一条边的两个顶点都至少有一个顶点在 $S$中，则集合 $S$称为图的点覆盖集。一个图中所有的点覆盖集中点数最少的集合称为图的最小点覆盖。

证明： $点独立集 ≡_{P}点覆盖$

$\quad$由 $S$是点独立集证明 $V-S$是点覆盖
$\quad$证明：设 $S$是大小为 $k$的点独立集。则对于图中的任意一条边 $(u,v)\in E$，因为 $S$是点独立集，故 $u,v$不能全在 $S$中，即 $u,v$至少有一个在 $V-S$中。因此，集合 $V-S$能保证对于图中每一条边，该边都至少有一个顶点在 $V-S$中， $V-S$是图的点覆盖。
$\quad$由 $V-S$是点覆盖证明 $S$是点独立集
$\quad$证明：设 $V-S$是大小为 $n-k$的点覆盖。则对于图中的任意一条边 $(u,v)\in E$， $(u,v)$至少有一个顶点在 $V-S$中，故在 $S$中， $(u,v)$最多有一个顶点在 $S$中。因此， $S$是图的点独立集。
$\quad$综上， $点独立集 ≡_{P}点覆盖$。

3、集合覆盖问题和顶点覆盖问题

$\quad$问题说明：给定一个集合 $U$和若干 $U$的子集合 $S_n$，问能否在 $S_n$中找出 $k$个集合，使得这 $k$个集合的并为 $U$。如下图所示，

集合 $S_c.S_f$的并为集合 $U$。
$\quad$定义了集合覆盖问题，我们可以将顶点覆盖问题规约到这个问题上去。即证明 $顶点覆盖 \le_{P} 集合覆盖$。这个问题的证明可以通过如下构造来完成：

• 顶点覆盖问题即为对于给定的图 $G=(V,E)$，能否找到 $k$个点，使得图中每条边都至少有一个点在这 $k$个点中。
• 对于顶点问题做如下转化：给定一个集合 $U$， $U$中元素为图中的每条边。对于图中每个顶点 $i$，我们都建立一个集合 $S_i$， $S_i$中元素为与顶点 $i$相连的边。这样，问题就转化成了在集合 $S$中能否找到 $k$个集合，使得这些集合的并为 $U$。
• 举个例子，下图是一个6个顶点，7条边的图。对于左边的图而言，当 $k=2$时， ${c,f}$为图的点覆盖；对于右边转化后的集合而言， $S_c,S_f$的并集为 $U$。
  
  $\quad$这样，就证明了顶点覆盖 可以多项式规约到集合覆盖。但集合覆盖问题能多项式规约到顶点覆盖问题吗？答案是否定的，因为对于任意的集合 $S_i$而言，每个元素出现次数可能不是偶数，对于图而言，每条边出现次数一定是偶数，故这种情况下无法通过构图来表示任意一种集合，因此集合覆盖无法规约到顶点覆盖。

4、可满足性问题(SAT)和3-SAT

$\quad$可满足性问题定义：对于给定的由二元bool变量构成的表达式，例如 $\Phi=C_1\wedge C_2 \wedge C_3 \wedge C_4,C_i=x_1\vee \overline{x_2} \vee x_3$。 $x_i$为bool变量，目的是求解合适的 $x_i$的值，使得 $\Phi=true$。 $\wedge$表示“与”， $\vee$表示"并"， $\overline{x}$表示 $x$的非。由此可知，要使得 $\Phi=true$，那么每个 $C_i=true$，进而得到每个 $C_i$中二元变量 $x_i$至少有一个为 $true$。
$\quad$ 3-SAT：当每个 $C_i$包含3个bool变量时构成的逻辑表达式 $\Phi$，并求解各个bool变量使得 $\Phi=true$的问题称为3-SAT问题。如下图即为一个3-SAT问题及其的一个解。

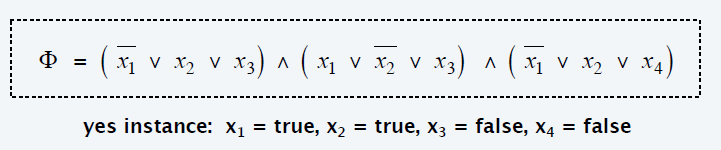
证明： $3-SAT\le_{P}点独立集问题$

5、自规约问题

规约问题总结

$\quad$规约的传递性：若 $X\le_{P}Y,Y\le_{P}Z$，则 $X\le_{P}Z$。
$\quad$对上面规约问题做一个总结： $3-SAT\le_{P}点独立集问题\le_{P}顶点覆盖问题\le_{P}集合覆盖问题$

二、P，NP和NPC问题

1、P问题

$\quad$能在多项式时间内解决的问题称为P问题。比如：素数问题。
素数问题：任意给定一个数字 $s$，求 $s$是否是素数的算法。AKS素数测试（又被称为 Agrawal–Kayal–Saxena素数测试 和 Cyclotomic AKS test）是一个决定型素数测试算法 ，由三个来自印度坎普尔理工学院的计算机科学家，Manindra Agrawal、Neeraj Kayal和Nitin Saxena，在2002年8月6日发表于一篇题为素数属于P的论文。

2、NP问题

$\quad$能在多项式时间内验证的问题称为NP问题。比如：对于3-SAT问题，给出其中一个解法，让你判断这个解法是否是原问题的一个解。可见所有的P问题都可以在多项式时间内去验证，因此，P问题是NP问题的子集。

3、EXP问题

$\quad$能在指数时间复杂度内解决的问题。NP问题是EXP问题的子集。

4、普遍认为 $P\neq P$

$\quad$目前还不能证明 $P=NP$或者 $P \neq NP$。

5、NPC问题

$\quad$找出一个已被证明的NPC问题(SAT)，所有能规约到这个NPC问题的问题统称为NPC问题。
$\quad$定理：若 $X$是NPC问题， $Y$是NP问题， $X \le_{P} Y$，则 $Y$是NPC问题。

三、经典的NPC问题

1、序列问题

$\quad$哈密尔顿圈：对于给定的图 $G$，问是否存在一条路，使得经过图 $G$所有顶点并且每个顶点只经过一次。