神马是状态压缩?
就是当普通dp的每一维表示的状态非常少的时候,可以压缩成一维来表示

如果m==8
dp[i][0/1][0/1]......[0/1]
压缩一下
dp[i][s]表示到了第i行,状态是s的方案数

那么状态数是指数级的
有点大.......
考虑每一行的合法状态真的有那么多吗?
考虑只有一行的情况
m: 0 1 2 3 4 5 6 7
f: 1 2 3 5 8 13 21 34
为什么方案数f是斐波那契数列呢?
因为f[i]可以是由f[i-1]再加1个0或者由f[i-2]再加1个01得到

设dp[i][s]为填到第i行,状态为s的状态
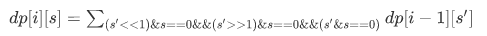
.....
说人话:
将s'左移一下,右移一下看一看是否会攻击到s即可
还可以这样判断:(s|s<<1|s>>1)&s'==0的s'是可行的
s是上下攻击,s<<1是在s'左边,s>>1是在s'右边
神奇的位运算

6为什么是枚举子集?
s0每次去掉二进制表示的最后一个1,再和原集进行&操作,就去掉了新的s0的不属于s的部分,同时每次只减去1个1就没有重复
复杂度是![]()
震惊!!!
我们看这个循环,s是枚举有n位的二进制数,它一共有s个1,s0枚举它的子集,子集有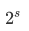 个
个
总数: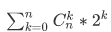
变一变形: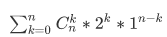
这就是二项式定理啊
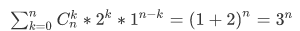

看起来n比较小,可以压n的样子
dp[s]表示s这个集合拓扑序的个数
转移:考虑枚举一个点u,加进拓扑序
u满足:1:不在s里面;2:能到达u的点都在s里面
复杂度: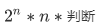
怎么快速判断?
预处理in[u],表示能够到达点u的点组成的集合,当s&in[u]==in[u]时,就是所有能到达u的点都在s里面了

我们可以把每个数拆成q*2x*3y
当q不同的时候,两个数肯定不同,当q相同的时候,就把q提出来。
我们列个表
然后我们可以以行/列/斜着搞dp(就是有i层,不能选相邻的,就转化成了第一个问题)
但是具体选哪个呢?
先考虑列的复杂度:log2n<=17,转移:216
一行一行的:logn<=10:要压到311
当然下一行会少一点,是fib[10](斐波那契第10项)
为什么是fib???
现在问题已经转化成一层内不能选两个相邻的格子的问题了,这个问题的方案数就是fib[这一行的格子数]
我们发现行的复杂度要优一点(虽然依旧玄学),所以我们一行一行的dp
神仙斜着dp
当q>1,等价于q'=1&&n'=n/q。
◦剪枝:对于n/q相同的q,可以避免重复计算来加速。
打过一个表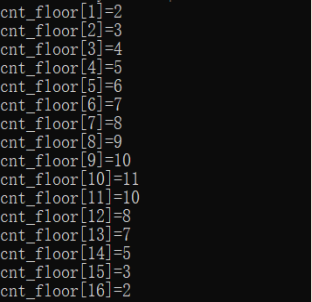
我们看到最宽的一层第10层宽度只有11,这个范围显然是可以
2^cnt_
NOIP 2016愤怒的小鸟

意思就是选最少的猪的集合,使得这些猪并起来是全集
有用的抛物线:n2个
dp[s]:集合s的猪被消灭最少用的抛物线
枚举包含s最低位的1抛物线t[i],(t[i]代表抛物线i经过的点的集合)
dp[s]=min(dp[s^t[i]]+1)(t[i]&s=t[i]且t[i]包含s的最低位)
这是按照s的最低位来分类,既然我们选了t[i]的点,之前就是dp[s^t[i]],再+1代表用了i这条抛物线
复杂度:2n*n

求出最少的合法的货物集合,使得并起来是原集
和上一个题很像啊
这里我们找出可以被一次运走的货物集合t
再套用上一个题的dp方程
复杂度:3n
枚举子集的复杂度是3n
用f[s]表示s是否能被c1运走,g[s]表示是否能被c2运走
t[s]表示s是否能被两辆车运走(这里是必须用两辆车)
t[s]=|s'f[s']&g[s^s'](s'是s的子集)(|是或运算)
枚举s的子集,看这个子集和s去掉这个子集之后的另一部分能否分别被两辆车运走
分子集的方案有一个满足就够了,所以是用或运算
复杂度3n
bzoj3900

仿佛看见两把刷子

设p[s]表示s集合的麋鹿内部能否交换成合法的麋鹿
排个序,看相邻两个的重量之差是否小于c
如果是,就说明有答案
但如果相邻的两个茸角不属于同一个麋鹿呢?
那最多需要n-1次搞定所有的麋鹿
g[s]表示使s内部消化的最小次数
g[s]≤s内部的人数 -1
那怎么转移呢?
我们不妨先试着把s分成几部分
我们发现s每分出去一部分合法的s',那g[s]至少会-1
why?
举个例子
设s集合原本有t个人,g[s]初始化为t-1
把t分为2部分:t-v,v
那g[v]最坏为v-1,g[t-v]最坏为t-v-1
g[v]+g[t-v]=v-1+t-v-1=t-2
所以每分出去一部分合法的s',g[s]至少会-1
那g[s]=min{g[s']+g[s^s']}(s'∈s)

dp[s][u]:s是三进制数,表示对应位上的点经过几次,u表示现在在哪个点
dp[s][u]=min(dp[s-(1<<i)][i]+dis[i][u])

包肯定是从大到小排序的
f[s]表示装下s的物品,用了多少包
g[s]表示装s的物品,用的最后一个包的剩下的最大空间
转移:看下一个物品能否装在当前的包里面,能则只更新g,否则加一个包,再更新g
dp优化


dp[i][j]表示长度为i,逆序对为j的排列数
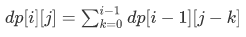
我们考虑新来的数插在哪里
原序列:a1,a2,a3....ai-1
放在
我们发现dp[i][j-k]是连续的耶
来个前缀和优化
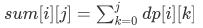
dp[i][j]=sum[i-1][j]-sum[i-1][j-i]



前缀和:区间的和
单调队列:区间最大值

f[i]表示到第i棵树的最小劳累值
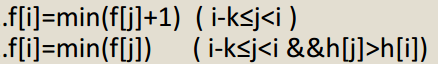
单调队列维护dp值小的,如果dp值相同,选高度要高的

经典的线段覆盖???
显然不是
不过我们还是要按照左端点排序
优化
dp[i][j]表示排完序之后,到了第i条线段,覆盖完前j个位置的方案数
后面*2
前面的累加
发现是区间*2,区间求和
然后就是线段树2的板子

简单的说就是一张纸条要走两次,不能经过重复的点,求经过的点的最大权值
暴力四维dp:

精简一维:
记录步数,第一次的横坐标,第二次的横坐标,然后按照上面的dp即可

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> #include<cmath> #include<queue> #include<set> #include<map> #define ll long long using namespace std; inline int read() { char ch=getchar(); int x=0;bool f=0; while(ch<'0'||ch>'9') { if(ch=='-')f=1; ch=getchar(); } while(ch>='0'&&ch<='9') { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return f?-x:x; } int n,m,ma[60][60],f[200][60][60]; int main() { m=read();n=read(); for(int i=1;i<=m;i++) for(int j=1;j<=n;j++) ma[i][j]=read(); for(int k=1;k<=n+m-1;k++) { for(int i=1;i<=k;i++) { for(int j=1;j<=k;j++) { int ex1=max(f[k-1][i][j],f[k-1][i-1][j-1]); int ex2=max(f[k-1][i-1][j],f[k-1][i][j-1]); f[k][i][j]=ma[i][k-i+1]+ma[j][k-j+1]+max(ex1,ex2); if(i==j)f[k][i][j]-=ma[i][k-i+1]; } } } printf("%d",f[n+m-1][m][m]); }
