宏观理解
LDA有两种含义
- 线性判别器(Linear Discriminant Analysis)
- 隐含狄利克雷分布(Latent Dirichlet Allocation,简称LDA)
本文讲解的是后者,它常常用于浅层语义分析,在文本语义分析中是一个很有用的模型。
LDA模型是一种主题模型,它可以将文档集中的每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题(分布)出来后,便可以根据主题(分布)进行主题聚类或文本分类。同时,它是一种典型的词袋模型,即一篇文档是由一组词构成,词与词之间没有先后顺序的关系。
上面的大家在任何的地方都能看到一句话,然鹅我在第一看的时候一点都没有看懂。
如果用通俗的语言来讲,假设我们有一个文档集,里面有M个文档,对于第d个文档中会出现一堆单词,其中有一个单词是“周杰伦”,那么通过这个单词我们就可以理解为该文档的主题可能是“娱乐”,但是这个文档中还出现“姚明”,“孙杨”,“张继科”这些单词,此时该文档为“体育”主题的概率将大大上升,LDA模型就是要根据给定一篇文档,推断这个文档的主题是什么,并给出各个主题的概率大小是多少。
那么对于我们刚刚提到的文档,“周杰伦”,“姚明”,“孙杨”,“张继科”,为”娱乐“主题的概率为1/4,为“体育”主题的概率为3/4,此时的LDA模型就说这个文档的主题为"体育"。
这样一想其实LDA主题模型的想法非常简单,但是具体到内部的细节,还是会有点懵。
琐碎但必要的知识
Gamma函数
这个Gamma函数其实是为后面的Beta分布和Dirichlet分布做准备,具体它的数学之美我们就不在本文讨论,只需要记住以下的东西
Gamma函数定义:
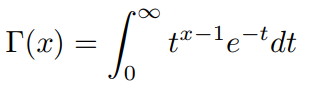
通过分部积分的方法,可以推导出这个函数有如下的递归性质:

于是gamma函数可以当成是阶乘在实数集上的延展,具有如下性质:
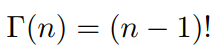
Beta分布
此时我们先引出个数学概念
- 在贝叶斯流派中,如果先验分布和后验分布是同类,则先验分布和后验分布被称为共轭分布,先验分布被称为似然函数的共轭先验
什么是Beta分布,它是指一组定义在$(0,1)$区间的连续概率分布,有两个参数$\alpha,\beta>0$,通俗的解释,beta分布可以看作一个概率的概率分布,当你不知道一个东西的概率是多少,它给你指出了所有可能出现的概率的概率大小,它的概率密度函数为
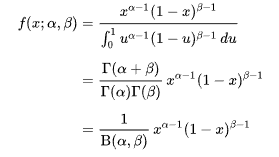
其中Bete函数为
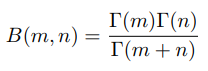
Beta分布是二项分布的共轭先验分布,Beta分布描述了二项分布中P取值的可能性,对于Betaf分布的随机变量,其均值可以估计为

Beta-Binomial共轭
首先我们要记住贝叶斯参数估计的基本过程为:
先验分布+数据的知识=后验分布
更一般的,对于非负实数$\alpha,\beta$,我们有如下关系:
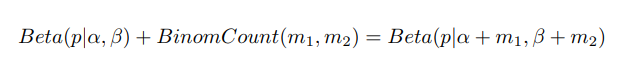
我们可以看到,参数的先验分布和后验分布都能够保持Beta分布的形式。
Dirichlet分布
狄利克雷分布是一组连续多变量概率分布,是多变量普遍化的Beta分布。
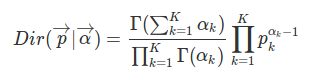
其中$\vec\alpha$是Dirichlet分布的参数。Dirichlet分布是多项式分布的共轭先验分布。
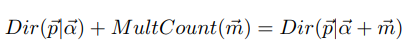
它的期望为
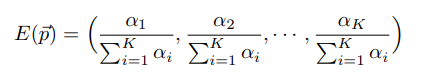
细致详解
- 每一篇文档的主题分布
- 每一个主题中单词的分布
我假定一个主题数目为K,这样所有的分布都是基于K个主题展开。
LDA假设文档主题的先验分布是DIrichlet分布,即对于任一文档$d$,其主题分布$\theta_d$为:
$$\theta_d = Dirichlet(\vec \alpha)$$
其中,$\alpha$为分布的超参数,是一个$K$维向量。
LDA假设主题中词的先验分布是DIrichlet分布,即对于任一主题$k$,其词分布$\beta_k$为:
$$\beta_k= Dirichlet(\vec \eta)$$
其中,$\eta$为分布的超参数,是一个$V$维向量,$V$代表词汇表里所有词的个数。
对于数据中任一一篇文档$d$中的第$n$个词,我们可以从主题分布$\eta_d$中得到它的主题编号$z_{dn}$的分布为:
$$z_{dn}=multi(\theta_d)$$
而对于该主题编号,得到我们看到的词$w_{dn}$的概率分布为:
$$w_{dn}=multi(\beta_{z_{dn}})$$
理解LDA主题模型的主要任务就是理解上面的这个模型,这个模型,我们有$M$个文档主题的Dirichlet分布,而对应的数据有$M$个主题编号的多项分布,这样($\alpha \to \theta_d \to \vec z_{d}$)就组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。
如果在第$d$个文档中,第$k$个主题的词的个数为:$n_d^{(k)}$,则对应的多项分布的计数可以表示为
$$\vec n_d = (n_d^{(1)}, n_d^{(2)},...n_d^{(K)})$$
利用Dirichlet-multi共轭,得到$\theta_d$的后验分布为:
$$Dirichlet(\theta_d | \vec \alpha + \vec n_d)$$
同样的道理,对于主题与词的分布,我们有$K$个主题与词的Dirichlet的分布,而对应的数据有$K$个主题编号的多项分布,这样($\eta \to \beta_k \to \vec w_{(k)}$)就组成了组成了Dirichlet-multi共轭,可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的主题词的后验分布。
如果在第k个主题中,第v个词的个数为:$n_k^{(v)}$,则对应的多项分布的计数可以表示为:
$$\vec n_k = (n_k^{(1)}, n_k^{(2)},...n_k^{(V)})$$
利用Dirichlet-multi共轭,得到$\beta_k$的后验分布为:
$$Dirichlet(\beta_k | \vec \eta+ \vec n_k)$$
由于主题产生词不依赖具体某一个文档,因此文档主题分布和主题词分布是独立的。理解了上面这$M+K$组Dirichlet-multi共轭,就理解了LDA的基本原理了。
参考资料
[1] 通俗理解LDA主题模型