V1 严正免责声明
本文部分内容摘自百度百科,经申明后免责。
V2 扯淡兼吐槽
想体验一下什么是绝望吗?
尝试做一下这道题,保证让你怀疑人生。QwQ
(大佬请跳过)
以下是正题
(超级详细)
1 概念性 查看详细点击
1.1 平衡二叉树
平衡二叉树( Balanced Binary Tree )具有以下性质:
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、 Treap 、伸展树等。
因为蒟蒻只会 Treap 并且 Treap 还不熟练,所以用了 Treap 。
1.2 Treap
Treap 是一棵二叉排序树,它的左子树和右子树分别是一个 Treap 。
和一般的二叉排序树不同的是, Treap 纪录一个额外的数据,就是优先级。
Treap 在以关键码构成二叉排序树的同时,还满足堆的性质
(在这里我们假设节点的优先级大于该节点的孩子的优先级)。
并且, Treap 具有“ BST 性质”:
-
该节点的关键码不小于它的左子树中任意节点的关键码;
-
该节点的关键码不大于它的右子树中任意节点的关键码。
2 过程
2.1 定义
这棵 Treap 要求支持以下操作:
-
插入 x 数
-
删除 x 数(若有多个相同的数,应只删除一个)
-
查询 x 数的排名(排名定义为比当前数小的数的个数 +1+1 。若有多个相同的数,应输出最小的排名)
-
查询排名为 x 的数
-
求 x 的前驱(前驱定义为小于 x ,且最大的数)
-
求 x 的后继(后继定义为大于 x ,且最小的数)
所以我们需要定义以下结构体变量(原因我在后面会解释)
1 struct Treap 2 { 3 int l,r,val,data,num,size; 4 }t[100005];
l :左孩子
r :右孩子
val :节点的关键码
data :节点的优先级
num :有多少个与当前节点的val相等的节点(自身要算入),即它的 $“副本数”$
size :节点有多少个后辈(自身要算入)
得到一个新的点
- 深度++;
- 赋值;
- 随机分配优先级;
- 副本数为1(算入自身)
- Size为1(算入自身)
1 int Get_New(int val) 2 { 3 ++law; 4 t[law].val=val; 5 t[law].data=rand(); 6 t[law].num=1; 7 t[law].size=1; 8 return law; 9 }
求Size
Size=左孩子的Size+右孩子的Size+自身的副本数。
1 void Update(int &p) 2 { 3 t[p].size=t[t[p].l].size+t[t[p].r].size+t[p].num; 4 }
建树
-
插入一个大小为负无穷的点(根节点)
-
插入一个大小为正无穷的点(根节点的右节点)
目的是为了防止平衡树退化成链
1 void Building() 2 { 3 Get_New(INT_MIN); 4 Get_New(INT_MAX); 5 root=1,t[1].r=2; 6 Update(root); 7 }
2.2 插入元素
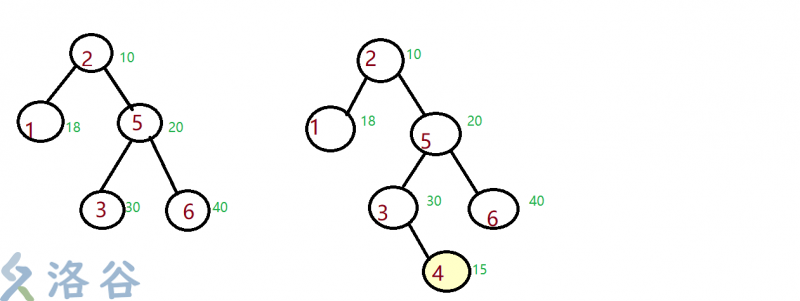
2.2.1 介绍
如上图所述,有一棵平衡二叉树,圆圈内黑色数代表节点的关键码,
圆圈旁红色的数代表节点的优先级(假设还没有维护根堆的性质)。
此时,把数4插入平衡二叉树。
2.2.2 插入的规则
为什么4要变成3的右儿子呢?
这时,就要用到二叉查找树树的“ BST 性质”。( 1.21.2 已解释,不赘)
在数据中,4>2,所以4不能成为1的儿子。又4<5,4所以不能成为6的儿子。
在所有叶子结点中,只有3满足了。又因为4>3,所以4成为3的右儿子。
并且,每个插入的节点有且仅有一个合适的位置。
2.3 左旋与右旋

2.3.1 旋转的缘由
显而易见,用随机数函数rand()函数分配平衡树Treap的优先级,并不能保证小根堆的性质,即节点A的优先级数有可能会比它的孩子节点的优先级数大。
为了维护小根堆的性质,必须对Treap进行左旋、右旋的操作。
2.3.2 旋转的法则
那么,什么时候应当进行左旋,而什么时候应当进行右旋呢?
我们先来研究上面的图。图中是对3进行左旋,旋转之后4代替了3原来的位置。
答案于是清楚了。因为3的优先级(即30)比4的优先级(即15)大,不具备小根堆的性质,于是将它左旋。
总的来说可以这样概括什么时候要进行左旋,什么时候要进行右旋:
A的右孩子的优先级数比A的优先级数大时要左旋
A的左孩子的优先级数比A的优先级数大时要右旋
2.3.3 旋转的过程
2.3.3.1 左旋
-
A的左孩子变成A左孩子的右孩子;
-
A左孩子的右孩子的值变成A的值;
-
A的值变成A的左孩子的值。
2.3.3.2 右旋
-
A的右孩子变成A右孩子的左孩子;
-
A右孩子的左孩子的值变成A的值;
-
A的值变成A的右孩子的值;
2.3.3.3 总结
显然,左旋和右旋的操作是完全相反的。
综上 2.2 及 2.3 ,我们可以得出旋转操作与插入操作的代码
1 void Zig(int &p) //右旋 2 { 3 int q=t[p].l; 4 t[p].l=t[q].r; 5 t[q].r=p; 6 p=q; 7 Update(t[p].r); //得到右孩子的Size 8 Update(p); //因为更新了位置,所以要更新p的Size 9 } 10 void Zag(int &p) //左旋 11 { 12 int q=t[p].r; 13 t[p].r=t[q].l; 14 t[q].l=p; 15 p=q; 16 Update(t[p].l); //得到右孩子的Size 17 Update(p); //同上 18 } 19 void Insert(int &p,int val) 20 { 21 if(p==0) //节点不存在并已经找到其应有位置 22 { 23 p=Get_New(val); 24 return ; 25 } 26 if(val==t[p].val) 27 { 28 t[p].num++; //节点已经存在 29 Update(p); //本身的Size 30 return ; 31 } 32 if(val<t[p].val) //当前节点的关键码大了 33 { 34 Insert(t[p].l,val); //往左边寻找合适的位置 35 if(t[p].data<t[t[p].l].data) 36 Zig(p); //旋转 37 } 38 else 39 { 40 Insert(t[p].r,val); //往右边寻找合适的位置 41 if(t[p].data<t[t[p].r].data) 42 Zag(p); //旋转 43 } 44 Update(p); //更新p的Size 45 }
2.4 删除
这个操作即是原题中的操作 22
对于一棵树而言,删除一个节点显得并不是那么简单。
如果需要删除的是叶子节点,那么是比较方便的,只需要删除该节点。
而如果现在需要删除的节点有孩子,那么就比较麻烦了,还需要对它的孩子节点处理。
当然,同插入一样,删除操作也是以递归方法实现。
2.4.1 过程
那么有以下过程:
-
如果要删除的关键码对应的节点不存在,则直接返回。
-
如果找到了该节点
-
如果该节点的“副本数”多于1,则让它的“副本数”减一
-
如果该节点有孩子节点,即不是叶子节点: 如果左节点的优先级大于右节点的优先级或不存在右节点,就右旋。 因为右旋可以让左节点代替自己(见 2.32.3 )。 然后删除左节点的右节点的值(即右旋后的右节点)。 如果相反则相反地操作,不赘。
-
则该节点为叶子节点,直接删除。
-
-
则没有找到
-
如果当前关键码比要寻找的关键码大,就朝左边找;
-
如果当前关键码比要寻找的关键码小,就朝右边找;
-
2.4.2 代码
由上述过程得到代码:
1 void Remove(int &p,int val) 2 { 3 if(p==0) return ; 4 if(val==t[p].val) 5 { 6 if(t[p].num>1) 7 { 8 t[p].num--; 9 Update(p); 10 return ; 11 } 12 if(t[p].l||t[p].r) 13 { 14 if(t[p].r==0||t[t[p].l].data>t[t[p].r].data) 15 { 16 Zig(p); 17 Remove(t[p].r,val); 18 } 19 else 20 { 21 Zag(p); 22 Remove(t[p].l,val); 23 } 24 Update(p); 25 } 26 else p=0; 27 return ; 28 }
2.5 由值得出排名
显然,这种操作是要寻找排名的,
所以,这个操作基于查询。
2.5.1 过程
-
如果该节点不存在,直接返回
-
如果找到了,就返回左节点的Size+1
为什么是这样呢?
因为该节点的左子树的所有节点的关键码都比自己小,左节点的最大子树就是它的Size
所以此时,Size就发挥了作用。
又因为该节点的右子树的每个节点的关键码都比该节点的关键码大,所以与该节点的排名无关。
而左节点的Size是包括左节点在内的左子树节点个数,也是比该节点的关键码的小的节点个数。
就如一个数列中最大数没有其他数比他大,而它的排名是一,所以还要加一。
-
如果找到了,那么又是一样的套路:
-
如果当前关键码比要寻找的关键码大,就朝左边找;
-
如果当前关键码比要寻找的关键码小,就朝右边找;
2.5.2 代码:
1 int Sortt(int &p,int val) 2 { 3 if(p==0) 4 return 0; 5 if(val==t[p].val) 6 return t[t[p].l].size+1; 7 if(val<t[p].val) 8 return Sortt(t[p].l,val); 9 return Sortt(t[p].r,val)+t[t[p].l].size+t[p].num; 10 }
2.6 由排名得出值
这个操作同 2.52.5 一样,也是基于查询的,但是查询的不是排名,而是节点的值。
2.6.1 过程
那么,过程也很好给出。
-
如果不存在该节点,直接返回最大值(注意,不是0)
-
如果左节点的最大子树节点个数比要查询的排名大,就向左边寻找。
同样,说明一下理由:
易知,左节点的最大子树节点个数是当前节点关键码小的节点的个数,即它的排名-1.
如果它的要查询的排名比现在的排名小,说明当前节点的关键码比实际的答案大,于是向左节点查询。
- 如果左节点的最大子树节点个数与当前节点的副本数的和比要查询的排名大,就返回自己的关键码。
因为如果它的要查询的排名比现在的排名小,那么已经执行了第二个 ifif 语句,不会到这一步。
所以要查询的排名比现在的排名大,而加上自己的副本数就比现在排名小了。
所以,排名如果算上副本数,则要查询的排名是当前节点的所有副本的排名中的一个。
所以这个排名对应的节点就是当前节点或他的副本。
又因为当前节点的关键码和它的副本的关键码是相等的,所以返回当前节点的关键码。
2.6.2 过程
1 int Value(int &p,int rank) 2 { 3 if(p==0) 4 return INT_MAX; 5 if(t[t[p].l].size>=rank) 6 return Value(t[p].l,rank); 7 if(t[t[p].l].size+t[p].num>=rank) 8 return t[p].val; 9 return Value(t[p].r,rank-t[t[p].l].size-t[p].num); 10 }
2.7 求前驱
实话来说,求前驱和求后继是最好理解的。
前驱:定义为小于 x ,且最大的数。
通俗地来说,就是最接近 x 的比它小的数。
不难得到,它的主要特点就是比x小。
所以:
2.7.1 过程
-
先向当前节点的左节点寻找。
-
只要存在右节点,就往右边寻找。
过程1满足了比 x 小的性质,而过程2满足了最大的数。
2.7.2 代码
1 int Pre(int val) 2 { 3 int pre=1; 4 int p=root; 5 while(p) 6 { 7 if(val==t[p].val) 8 { 9 if(t[p].l>0) 10 { 11 p=t[p].l; 12 while(t[p].r>0) 13 p=t[p].r; 14 pre=p; 15 } 16 break; 17 } 18 if(t[p].val<val&&t[p].val>t[pre].val) pre=p; 19 if(val<t[p].val) 20 p=t[p].l; 21 else p=t[p].r; 22 } 23 return t[pre].val; 24 }
2.8 求后继
2.8.1 过程
和求前驱相反。
-
先向当前节点的右节点寻找。
-
只要存在左节点,就往左边寻找。
过程1满足了比 x 大的性质,而过程2满足了最小的数。
2.8.2 代码
int Suf(int val) { int suf=2; int p=root; while(p) { if(val==t[p].val) { if(t[p].r>0) { p=t[p].r; while(t[p].l>0) p=t[p].l; suf=p; } break; } if(t[p].val>val&&t[p].val<t[suf].val) suf=p; if(val<t[p].val) p=t[p].l; else p=t[p].r; } return t[suf].val; }
2.9 main函数
参照题意得:
int main() { std::ios::sync_with_stdio(false); //输入输出优化 Building(); cin>>m; while(m--) { int op,x; cin>>op>>x; if(op==1) { Insert(root,x); continue; } if(op==2) { Remove(root,x); continue; } if(op==3) { cout<<Sortt(root,x)-1<<endl; continue; } if(op==4) { cout<<Value(root,x+1)<<endl; continue; } if(op==5) { cout<<Pre(x)<<endl; continue; } if(op==6) { cout<<Suf(x)<<endl; continue; } } return 0; }
3 Code完整代码:
具体的我已经详细地讲解了一遍,所以干净地不加注释
1 #include<bits/stdc++.h> 2 #pragma GCC optimize(3) //手动吸臭氧 3 using namespace std; 4 struct Treap 5 { 6 int l,r,val,data,num,size; 7 }t[100005]; 8 int law,root,m; 9 int Get_New(int val) 10 { 11 ++law; 12 t[law].val=val; 13 t[law].data=rand(); 14 t[law].num=1; 15 t[law].size=1; 16 return law; 17 } 18 void Update(int &p) 19 { 20 t[p].size=t[t[p].l].size+t[t[p].r].size+t[p].num; 21 } 22 void Building() 23 { 24 Get_New(INT_MIN); 25 Get_New(INT_MAX); 26 root=1,t[1].r=2; 27 Update(root); 28 } 29 void Zig(int &p) 30 { 31 int q=t[p].l; 32 t[p].l=t[q].r; 33 t[q].r=p; 34 p=q; 35 Update(t[p].r); 36 Update(p); 37 } 38 void Zag(int &p) 39 { 40 int q=t[p].r; 41 t[p].r=t[q].l; 42 t[q].l=p; 43 p=q; 44 Update(t[p].l); 45 Update(p); 46 } 47 void Insert(int &p,int val) 48 { 49 if(p==0) 50 { 51 p=Get_New(val); 52 return ; 53 } 54 if(val==t[p].val) 55 { 56 t[p].num++; 57 Update(p); 58 return ; 59 } 60 if(val<t[p].val) 61 { 62 Insert(t[p].l,val); 63 if(t[p].data<t[t[p].l].data) 64 Zig(p); 65 } 66 else 67 { 68 Insert(t[p].r,val); 69 if(t[p].data<t[t[p].r].data) 70 Zag(p); 71 } 72 Update(p); 73 } 74 void Remove(int &p,int val) 75 { 76 if(p==0) return ; 77 if(val==t[p].val) 78 { 79 if(t[p].num>1) 80 { 81 t[p].num--; 82 Update(p); 83 return ; 84 } 85 if(t[p].l||t[p].r) 86 { 87 if(t[p].r==0||t[t[p].l].data>t[t[p].r].data) 88 { 89 Zig(p); 90 Remove(t[p].r,val); 91 } 92 else 93 { 94 Zag(p); 95 Remove(t[p].l,val); 96 } 97 Update(p); 98 } 99 else p=0; 100 return ; 101 } 102 if(val<t[p].val) 103 Remove(t[p].l,val); 104 else Remove(t[p].r,val); 105 Update(p); 106 } 107 int Sortt(int &p,int val) 108 { 109 if(p==0) 110 return 0; 111 if(val==t[p].val) 112 return t[t[p].l].size+1; 113 if(val<t[p].val) 114 return Sortt(t[p].l,val); 115 return Sortt(t[p].r,val)+t[t[p].l].size+t[p].num; 116 } 117 int Value(int &p,int rank) 118 { 119 if(p==0) 120 return INT_MAX; 121 if(t[t[p].l].size>=rank) 122 return Value(t[p].l,rank); 123 if(t[t[p].l].size+t[p].num>=rank) 124 return t[p].val; 125 return Value(t[p].r,rank-t[t[p].l].size-t[p].num); 126 } 127 int Pre(int val) 128 { 129 int pre=1; 130 int p=root; 131 while(p) 132 { 133 if(val==t[p].val) 134 { 135 if(t[p].l>0) 136 { 137 p=t[p].l; 138 while(t[p].r>0) 139 p=t[p].r; 140 pre=p; 141 } 142 break; 143 } 144 if(t[p].val<val&&t[p].val>t[pre].val) pre=p; 145 if(val<t[p].val) 146 p=t[p].l; 147 else p=t[p].r; 148 } 149 return t[pre].val; 150 } 151 int Suf(int val) 152 { 153 int suf=2; 154 int p=root; 155 while(p) 156 { 157 if(val==t[p].val) 158 { 159 if(t[p].r>0) 160 { 161 p=t[p].r; 162 while(t[p].l>0) 163 p=t[p].l; 164 suf=p; 165 } 166 break; 167 } 168 if(t[p].val>val&&t[p].val<t[suf].val) 169 suf=p; 170 if(val<t[p].val) 171 p=t[p].l; 172 else p=t[p].r; 173 } 174 return t[suf].val; 175 } 176 int main() 177 { 178 std::ios::sync_with_stdio(false); 179 Building(); 180 cin>>m; 181 while(m--) 182 { 183 int op,x; 184 cin>>op>>x; 185 if(op==1) 186 { 187 Insert(root,x); 188 continue; 189 } 190 if(op==2) 191 { 192 Remove(root,x); 193 continue; 194 } 195 if(op==3) 196 { 197 cout<<Sortt(root,x)-1<<endl; 198 continue; 199 } 200 if(op==4) 201 { 202 cout<<Value(root,x+1)<<endl; 203 continue; 204 } 205 if(op==5) 206 { 207 cout<<Pre(x)<<endl; 208 continue; 209 } 210 if(op==6) 211 { 212 cout<<Suf(x)<<endl; 213 continue; 214 } 215 } 216 return 0; 217 }
4 个人总结
希望大家看完这篇博客之后能够收获很多,本人编辑这篇博客用了一个多月的时间。
如果有什么不足,向诸位请教!!