主题模型

先做个总结：

一个函数。
四个分布：二项分布，多项分布，Beta分布，Dirichel分布。
一个概念和一个理念：共轭先验和贝叶斯框架。
两个模型：pLSA，LDA
一个采样：Gibbs采样

贝叶斯理论：先验分布+数据（似然）=后验分布
这点其实很好理解，因为这符合我们人的思维方式，比如你对好人和坏人的认知，先验分布为：100个好人和100个的坏人，即你认为好人坏人各占一半，现在你被2个好人（数据）帮助了和1个坏人骗了，于是你得到了新的后验分布为：102个好人和101个的坏人。现在你的后验分布里面认为好人比坏人多了。这个后验分布接着又变成你的新的先验分布，当你被1个好人（数据）帮助了和3个坏人（数据）骗了后，你又更新了你的后验分布为：103个好人和104个的坏人。依次继续更新下去。

LDA的原理

先导数学知识准备
文本模型 - Unigram Model
主题模型 - PLSA Model
主题模型 - LDA Model

1、先导数学知识准备

LDA之所以很难懂，跟其涉及大量的数学统计知识有关，因此，为了更好的理解LDA，还是先铺垫一些数学知识。本段力求少摆公式，用更通俗的话来阐述其背后的数学思想~

1 Gamma函数

认真学过高数的应该都对这个函数有印象，其基本公式如下：

$\Gamma (x) = \int_{0}^{\infty } t^{x-1}e^{-t}dt$
再贴一张Gamma函数图，方便大家对其有一个概览性的认识：

该函数有一个很好的递归性质（利用分步积分法可证）如下：

$\Gamma (x + 1) =x\Gamma(x)$
当然该函数还有更重要的一点，即其可以表述为阶乘在实数集上的延拓：

$\Gamma(n) = (n-1)!$

2 二项分布

高中学概率论的时候，还记得抛硬币的例子么？每一次抛硬币都会有俩个结果，正面OR背面，那么抛一次硬币就满足伯努利分布（又叫0-1分布），是一个离散型的随机分布。二项分布无非就是重复N次的伯努利实验，其概率密度函数可以表示为：

$P(K = k) = \begin{pmatrix} n\\ k\\ \end{pmatrix}p^k{(1-p)}^{n-k}$
其中p我们可以理解为好人的概率，k为好人的个数，n为好人坏人的总数
这就是我们的数据（似然）。
其中

$\begin{pmatrix} n\\ k\\ \end{pmatrix}=C(n,k) = \frac{n!}{k!(n-k)!}$
看到C(n,k)大部分人应该都能想起这个在高中就学过的式子的意思，最简单的排列组合，从n个事件中挑出k个事件的组合方式，因此上面的式子应该不难理解了。

共轭分布

虽然数据(似然)很好理解，但是对于先验分布，我们就要费一番脑筋了，为什么呢？因为我们希望这个先验分布和数据（似然）对应的二项分布集合后，得到的后验分布在后面还可以作为先验分布！就像上面例子里的“102个好人和101个的坏人”，它是前面一次贝叶斯推荐的后验分布，又是后一次贝叶斯推荐的先验分布。也即是说，我们希望先验分布和后验分布的形式应该是一样的，这样的分布我们一般叫共轭分布。

在我们的例子里，我们希望找到和二项分布共轭的分布。

和二项分布共轭的分布其实就是Beta分布。Beta分布的表达式为：
$Beta(p|\alpha,\beta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}p^{\alpha-1}(1-p)^{{\beta-1}}$

3 多项分布

高中学习概率论的时候，我们除了仍硬币还仍什么？还会仍骰子哈哈~但这个时候仍一次骰子就不满足伯努利分布了，因为仍一次骰子会有6或更多种结果。因此，多项分布就是二项分布扩展到高维的情况，其概率密度函数可以表示为：

$P(x_1, x_2, ..., x_k; n, p_1, p_2, ..., p_k) = \frac{n!}{x_1!...x_k!}{p_1}^{x_1}...{p_k}^{x_k}$

4 Beta分布

通俗理解，当我们不知道一个概率是什么，但又有一些合理的猜测时，Beta分布能很好的作为一个表示概率的概率分布。举个例子，我们要统计预测一下周琦新赛季的三分投篮命中率，假如周琦上赛季投了一个三分，命中一个，则按照我们熟悉的思路，我们可以预测琦琦新赛季命中率100%！但仔细一想不对啊，就算是顶级的三分手（比如汤神）也就40%超一点，难道我周琦比汤神还牛了？显然这里大家的思考就会出现分歧，于是就引申出了一个统计学知识点，或者说是俩个学派 - 频率学派和贝叶斯学派！这俩个学派的思路差异体现在：

频率学派：他们把需要推断的参数 $\theta$ （本例就是周琦的三分命中率）看做是固定的未知常数，即虽然这个概率是未知的，但却是确定的一个值，同时，样本 $X$ 是随机的，因此频率学派重点研究样本空间，大部分的概率计算都是针对样本 $X$ 的分布！
贝叶斯学派：他们与频率学派认知刚好相反，他们认为参数都不是固定值，而是服从一个概率分布，样本 $X$ 却是固定的，因此他们重点研究的是参数的分布。

因此，回到周琦的例子上来，用传统频率学派的观点，那周琦的命中率确实就是100%，而用贝叶斯学派的观点，首先周琦的命中率有一个先验分布，而根据样本信息，我们可以对其进行更新，得到后验分布。而数学家们为二项分布选取的先验分布就是Beta分布！

Beta分布在概率论中指一组分布在 $[0,1]$ 区间的连续概率分布，其中参数为 $\alpha > 0$ , $\beta > 0$ ，概率密度函数为：

$f(x; \alpha, \beta) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1} {(1-x)}^{\beta-1}$
其中，

$\frac{1}{B(\alpha, \beta)} = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}$
至于 $\alpha, \beta$ 代表的物理意义，可以简单理解这俩一起控制着Beta分布的形状，贴一张图方便理解：

不同取值的Beta分布如上图。

当然如果这个时候新赛季已经开打，那我们又会多得到一点信息，比如周琦在揭幕战怒投5三分，并且命中2个，错失3个，那这个时候，揭幕战中投出的5个三分，肯定能为我所用（样本信息为二项分布），用于更新我对周琦一开始命中率预测的 $Beta(\alpha, \beta)$ 分布。而这个时候就要用到Beta分布另一个重要的性质了，即Beta-Binomial共轭，对周琦的预测分布可更新为 $Beta(\alpha + 2, \beta + 3)$ 。

先讲明，“共轭分布” 援引wiki的定义即为：在贝叶斯统计中，如果后验分布与先验分布属于同类，则先验分布与后验分布被称为共轭分布，而先验分布被称为似然函数的共轭先验【1】。参照定义，Beta-Binomial 共轭意味着，如果我们为二项分布的参数p选取的先验分布是Beta分布，那么以p为参数的二项分布用贝叶斯估计得到的后验分布仍然服从Beta分布，那么Beta分布就是二项分布的共轭先验分布，用数学公式表述就是：

$Beta(p|\alpha,\beta) + BinomCount(m_1,m_2) = Beta(p|\alpha + m_1, \beta + m_2)$
这种形式不变的好处是，我们能够在先验分布中赋予参数很明确的物理意义，这个物理意义可以延续到后续分布中进行解释，同时从先验变换到后验过程中从数据中补充的知识也容易有物理解释【2】。另外再多说一点，关于Beta分布的期望可推导表示为：

$E(p) = \frac{\alpha}{\alpha + \beta}$
不知大家能否一眼看出这俩个参数的物理意义，实际上就是周琦三分投篮时候，命中与未命中的次数！

5 Dirichlet分布

终于涉及到本文的主角，Dirichlet分布了~。类比于多项分布是二项分布的推广，Dirichlet分布也确实是Beta分布的推广，其概率密度函数为：

$f(x_1, x_2, ..., x_k; \alpha_1, \alpha_2, ..., \alpha_k) = \frac{1}{B(\alpha)}\prod_{i=1}^{k}{x_i}^{\alpha^i-1}$

如果：
$Dirichlet(p_1,p_2,p_3|\alpha_1,\alpha_2, \alpha_3) = \frac{\Gamma(\alpha_1+ \alpha_2 + \alpha_3)}{\Gamma(\alpha_1)\Gamma(\alpha_2)\Gamma(\alpha_3)}p_1^{\alpha_1-1}(p_2)^{\alpha_2-1}(p_3)^{\alpha_3-1}$

那么：
$Dirichlet(\vec p| \vec \alpha) = \frac{\Gamma(\sum\limits_{k=1}^K\alpha_k)}{\prod_{k=1}^K\Gamma(\alpha_k)}\prod_{k=1}^Kp_k^{\alpha_k-1}$
且类比于Beta分布，Dirichlet也是多项分布的共轭先验分布：

$Dirichlet(\vec{p}|\vec{\alpha}) + MultiCount(\vec {m}) = Dirichlet(\vec{p}|\vec{\alpha} + \vec{m})$
相对应于Beta的期望，Dirichlet分布的期望也可以如下：（其物理意义也就是每个参数的估计值是其对应事件的先验的参数（也叫伪计数）和数据中的计数的和在整体计数中的比例）：

$E(p) =\biggl ( \frac{\alpha ^ 1}{\sum_{i = 1}^K \alpha_i}, \frac{\alpha ^ 2}{\sum_{i = 2}^K \alpha_i}, \cdots, \frac{\alpha ^ K}{\sum_{i = 1}^K \alpha_i} \biggr)$

2、文本模型 - Unigram Model

假设一篇文档由若干个词语构成，可以不考虑顺序，就你像看这句话的时候也没现发他序顺乱了~因此我们不妨就把一篇文章看作是一些词的集合。那么最简单的文本生成模型就是，确定文本的长度为N，然后选出N个词来。选词的过程与我们仍骰子一模一样，无非就是这个骰子的面比较多，但其仍然服从多项分布。这个简单的文本生成模型就叫做Unigram Model。当然少不了贝叶斯估计，每一个面朝上的概率也会有一个先验分布为Dirichlet分布，表示为 $Dir(\vec{p}|\vec{\alpha})$ ，而我们也可以根据样本信息 $\vec{n}$ 来估计后验分布 $Dir(\vec{p}|\vec{\alpha} + \vec{n})$ ，其概率图模型可以表示为：

Unigram Model 概率图模型

该记图方式为plate notation，有兴趣的可以了解一下。此时该文本的生成概率就等于：

$p(\vec{W}|\vec{\alpha}) = \int p(\vec{W}|\vec{p})\cdot p(\vec{p}|\vec{\alpha})d\vec{p}$
我们推导可以计算得到：

$p(\vec{W}|\vec{\alpha}) = \frac{\Delta (\vec{n} + \vec{\alpha}) }{\Delta (\vec{\alpha})}$

3、主题模型 - PLSA Model

上面讲的文本生成模型足够简单，但是对文本的表达能力还是不够，且不太符合我们日常的写作习惯！试想，我们写一篇文章的时候，肯定都会事先拟定一个主题，然后再从这个主题中去寻找相应的词汇，因此这么来看，只扔一个有N面的骰子似乎还不够，我们似乎应该提前再准备m个不同类型的骰子，作为我们的主题，然后确定了主题以后，再选中那个骰子，来决定词汇。由此，便引申出了我们的主题模型！

简单来说PLSA是用一个生成模型（生成模型与判别式模型的区别大家还是要懂的）来建模文章的生成过程！它有几个前提假设【3】如下：

一篇文章可以由多个主题构成
每一个主题由一组词的概率分布来表示
一篇文章中的每一个具体的词都来自于一个固定的主题

其概率图模型【4】可以表示为：

PLSA Model 概率图模型

用自己的话翻译一下上述过程就是：

按照概率 $P(d_i)$ 选中一篇文档 $d_i$
从主题分布中按照概率 $P(z_k|d_i)$ 选中一个主题 $z_k$
从词分布中按照概率 $P(w_j|z_k)$ 选中一个词 $w_j$

则整个语料库中的文本生成概率可以用似然函数表示为：

$L = \prod_{m}^{M}\prod_{n}^{N}p(d_m, w_n)^{c(d_w, w_n)}$
其中 $c(d_w, w_n)$ 表示单词 $w_n$ 在文档 $d_w$ 中出现的次数。

其对数似然函数可以写成：

$l = \sum_{m}^{M}\sum_{n}^{N}c(d_w, w_n)log\sum_{k}^{K}p(d_m)p(z_k|d_m)p(w_n|z_k)$
其中主题分布 $p(z_k|d_m)$ 和定义在主题上的词分布 $p(w_n|z_k)$ 就是待估计的参数，一般会用EM算法（值得另开一篇来单独讲的机器学习基础算法）来求解。

3、主题模型 - LDA Model

坚持看到这里的读者，其实内心应该对LDA也有了自己的猜想，看看PLSA漏了什么？没错，就是一个贝叶斯框架！如果我们给主题分布加一个Dirichlet分布 $\alpha$ ，再给主题上的词分布再加一个Dirichlet分布 $\beta$ ，那就是LDA！因此实际上LDA就是PLSA的贝叶斯版本。我们直接来看模型图【4】：

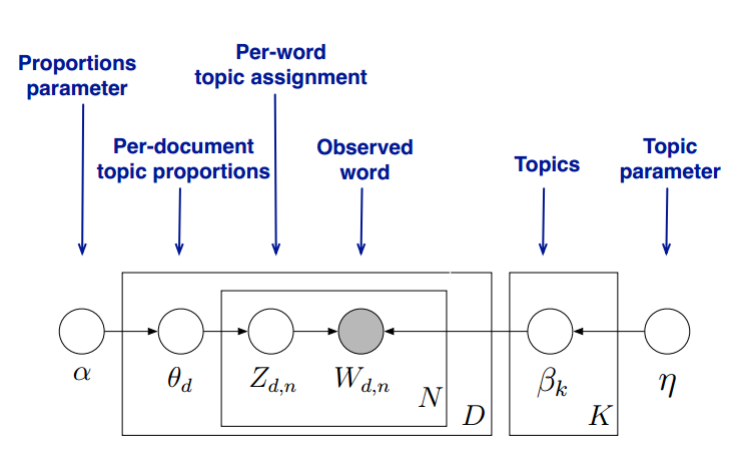
LDA Model 概率图模型

解释一：（如图左）

用自己的话翻译一下上述过程就是：

按照概率 $P(d_i)$ 选中一篇文档 $d_i$
从Dirichlet分布 $\alpha$ 中抽样生成文档 $d_i$ 的主题分布 $\theta_m$
从主题分布 $\theta_m$ 中抽取文档 $d_i$ 第j个词的主题 $z_{m,n}$
从Dirichlet分布 $\beta$ 中抽样生成主题 $z_{m,n}$ 对应的词分布 $\varphi_{k}$
从词分布 $\varphi_{k}$ 中抽样生成词 $w_{m,n}$

为了方便求解，我们通常会将上述过程顺序交换一下，即我们先生成完全部的主题，再由这些主题去生成完每一个词。这样，第一，二个过程的推导就可以用到Unigram Model的结论，即我们整个语料库下所有词的主题编号的生成概率为：

$p(\vec z \mid \vec \alpha) = \prod_{m}^{M}\frac{\Delta (\vec n_m + \vec \alpha)}{\Delta (\vec \alpha )}$
对于词的生成过程（主题编号的选择并不会改变K个主题下的词分布），即可表示为：

$p(\vec w \mid \vec z, \vec \beta) = p(\vec w \mid \vec \beta) = \prod_{k}^{V} \frac{\Delta (\vec v_k + \vec \beta )}{\Delta \vec \beta}$
因此，LDA模型的语料库的生成概率可以表述为：

$p(\vec w, \vec z \mid \vec \alpha, \vec \beta) = \prod_{k}^{K} \frac{\Delta (\vec v_k + \vec \beta )}{\Delta \vec \beta}\cdot \prod_{m}^{M}\frac{\Delta (\vec n_m + \vec \alpha)}{\Delta (\vec \alpha )}$

至此，整个LDA模型的文档生成过程介绍完了，而实际我们运用求解的时候，我们的任务也就是去估计隐含变量主题分布 $\vec \theta_m$ 和词分布 $\vec \varphi_k$ 的值了。实际求解的时候，一般会采用Gibbis Sampleing 。这里简单介绍一下，就是首先随机给定每个单词的主题，然后在其他变量保持不变的情况下，根据转移概率抽样生成每个单词的新主题，反复迭代以后，收敛后的结果就是主题分布和词分布的期望。

解释二：（如图右）

　LDA假设文档主题的先验分布是Dirichlet分布，即对于任一文档 d 其主题分布 $\theta_d$ 为：

$\theta_d = Dirichlet(\vec \alpha)$

　　　　其中，α 为分布的超参数，是一个 K 维向量。

　LDA假设主题中词的先验分布是Dirichlet分布，即对于任一主题 $k$ , 其词分布 $\beta_k$ 为：

$\beta_k= Dirichlet(\vec \eta)$

　　　　其中， $\eta$ 为分布的超参数，是一个 $V$ 维向量。 $V$ 代表词汇表里所有词的个数。

　对于数据中任一一篇文档 $d$ 中的第 $n$ 个词，我们可以从主题分布 $\theta_d$ 中得到它的主题编号 $z_{dn}$ 的分布为：

$z_{dn} = multi(\theta_d)$

　而对于该主题编号，得到我们看到的词 $w_{dn}$ 的概率分布为：

$w_{dn} = multi(\beta_{z_{dn}})$

　理解LDA主题模型的主要任务就是理解上面的这个模型。这个模型里，我们有 $M$ 个文档主题的Dirichlet分布，而对应的数据有 $M$ 个主题编号的多项分布，这样 $\alpha \to \theta_d \to \vec z_{d}$ 就组成了Dirichlet-multi共轭，可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。

　如果在第 d 个文档中，第 k 个主题的词的个数为： $n_d^{(k)}$ , 则对应的多项分布的计数可以表示为

$\vec n_d = (n_d^{(1)}, n_d^{(2)},...n_d^{(K)})$

　利用Dirichlet-multi共轭，得到 $\theta_d$ 的后验分布为：

$Dirichlet(\theta_d | \vec \alpha + \vec n_d)$

　同样的道理，对于主题与词的分布，我们有 $K$ 个主题与词的Dirichlet分布，而对应的数据有 $K$ 个主题编号的多项分布，这样 $\eta \to \beta_k \to \vec w_{(k)}$ 就组成了Dirichlet-multi共轭，可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的主题词的后验分布。

　如果在第 k 个主题中，第 v 个词的个数为： $n_k^{(v)}$ , 则对应的多项分布的计数可以表示为

$\vec n_k = (n_k^{(1)}, n_k^{(2)},...n_k^{(V)})$

　利用Dirichlet-multi共轭，得到 $\beta_k$ 的后验分布为：

$Dirichlet(\beta_k | \vec \eta+ \vec n_k)$

　由于主题产生词不依赖具体某一个文档，因此文档主题分布和主题词分布是独立的。理解了上面这 $M+K$ 组Dirichlet-multi共轭，就理解了LDA的基本原理了。

　现在的问题是，基于这个LDA模型如何求解我们想要的每一篇文档的主题分布和每一个主题中词的分布呢？

　一般有两种方法：
第一种是基于Gibbs采样算法求解。
第二种是基于变分推断EM算法求解。

[Python嗯~机器学习]---主题模型LDA基本理解

主题模型

猜你喜欢