数据结构--二叉树的概念与性质

概念

二叉树或为空树，或是有一个根节点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。

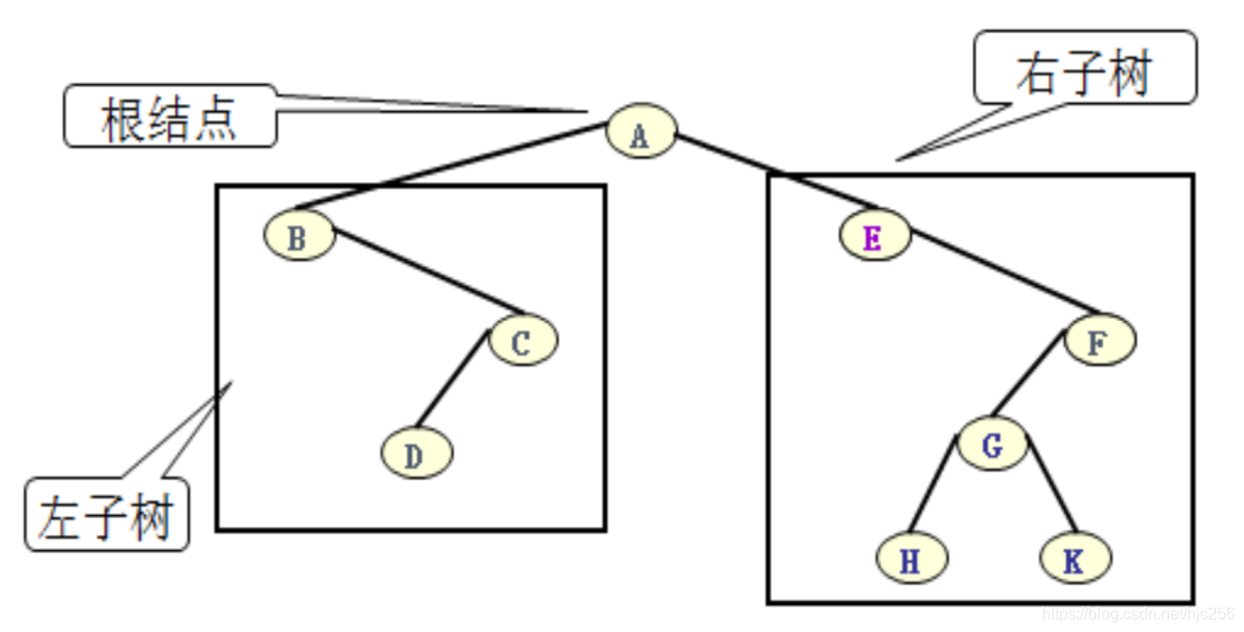
二叉树的五种基本形态

image

注：二叉树不等同于度不大于2的树，因为若两概念相同，则仅有左子树或仅有右子树的情况就是一种情况。

性质

性质1

在二叉树的第 $i$层上至多有 $2^{i-1}$个节点

性质2

深度为 $k$的二叉树上至多含有 $2^k-1$个节点。
（至少有k个节点）

证明：

思路就是让每一层都拥有最多的子树，即：
$2^0 + 2^1 + 2^3 + ...... + 2^{k-1} = 2^k - 1$

推广

满二叉树第 $k$层的节点个数比其第 1 ~ k-1层所有的节点多1个。

因为前 $k-1$层的子树和为 $2^0 + 2^1 + 2^3 + ...... + 2^{k-2} = 2^{k-1}$

而第 $k$层的子树有 $2^{k-1}$个。

性质3

对任何一个二叉树，若他含有 $n_0$个叶子节点， $n_2$个度为2的节点，则币存在关系式： $n_0 = n_2 + 1$

证明：

设二叉树上节点总数为： $n = n_0 + n_1 + n_2$

二叉树上的分支总数为： $b = n_1 + 2n_2$

又因为二叉树上的分支总数还可以等于： $b = n - 1 = n_0 + n_1 + n_2 - 1$

所以即可推出， $n_0 = n_2 + 1$。

推广

---

性质4

具有 $n$个节点的完全二叉树的深度为 $\lfloor log_2n \rfloor +1$

证明：

设完全二叉树的深度为 $k$

则根据性质2得： $2^{k-1} \le n \lt 2^k$，即 $k-1 \le log_2n \lt k$

又因为 $k$只能为整数，所以 $k = \lfloor log_2n。 \rfloor +1$

性质5

若对含 $n$个结点的完全二叉树从上到下且从左至右进行 1 至 $n$的编号， 则对完全二叉树中任意一个编号为 $i$的结点:

1. 若 $i=1$，则该结点是二叉树的根，无双亲， 否则，编号为 $\lfloor i / 2 \rfloor$的结点为其双亲结点;
2. 若 $2i \gt n$，则该结点无左孩子，否则，编号为 $2n$的结点为其左孩子结点;
3. 若 $2i+1 \gt n$，则该结点无右孩子结点，否则，编号为 $2i + 1$的结点为其右孩子结点。

特殊的二叉树

满二叉树

深度为 k 且含有 2k-1 个结点的二叉树

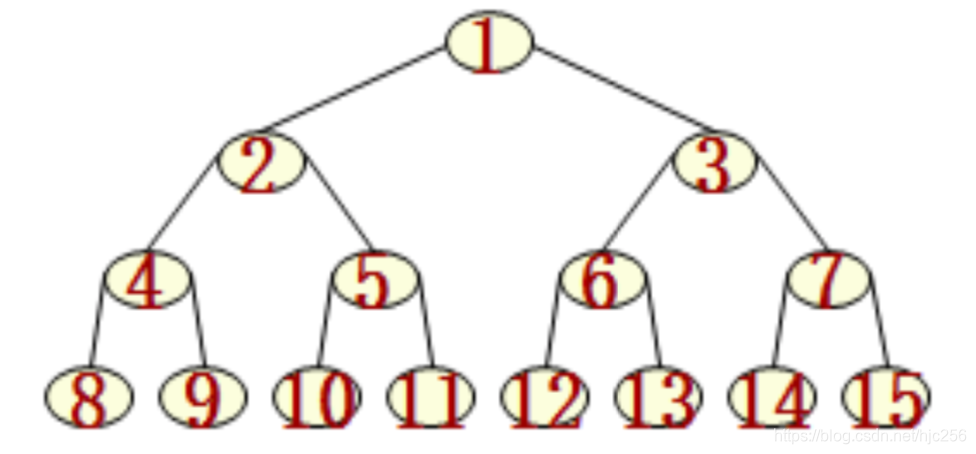
完全二叉树

树中所含的 n 个结点和满二叉树中编号为 1 至 n 的结点一一对应。

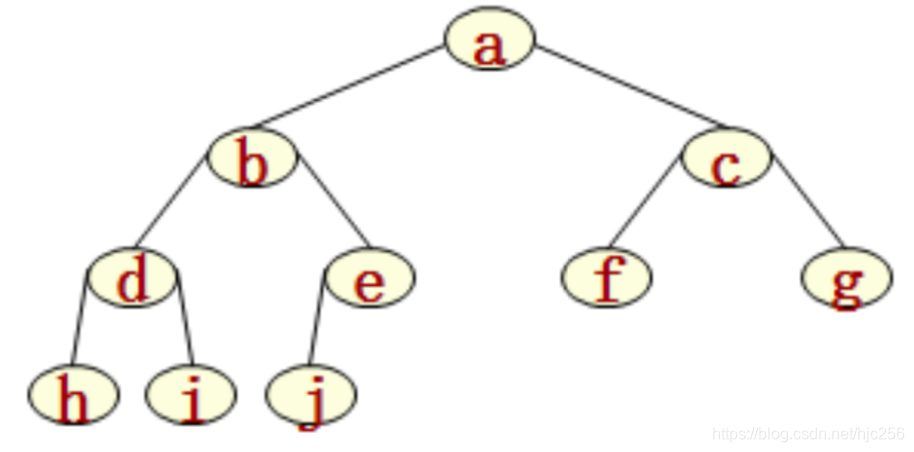
若完全二叉树有 $k$层，则前 $k-1$层都是满二叉树，第 $k$层集中在左部。叶节点只会出现在第 $k-1$层或第 $k$层。