[luogu P3868] [TJOI2009]猜数字

版权声明：蒟蒻写文章不容易啊，各位大佬转载要告诉我一声,QAQ https://blog.csdn.net/qq_38944163/article/details/85677874

我扔：https://www.luogu.org/problemnew/show/P3868

题意

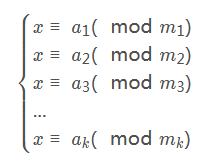
就是求这个 $x$
裸的中国剩余定理，什么？你不知道中国剩余定理。好吧，我讲讲。
首先，看上面那一坨式子，要满足

$m_1, m_2, m_3, ...., m_k$两两互质

那么我们设
$M = m1 \times m2 \times m3 \times .... \times mk$
$M_i = M / m_i$
则对于 $x \equiv a_i (\mod m_i)$, 我们可以先求出 $M_i 在 \mod m_i 意义下的逆元$（扩欧就行了）
设为 $M_i^{-1}$
可得 $M_i \times M_i^{-1} \equiv 1 (\mod m_i)$
所以 $a_i \times M_i \times M_i^{-1} \equiv a_i (\mod m_i)$
又因为 $M_i = M / m_i$
所以对于所有的 $j \neq i$ ( $j$ 不等于 $i$）
$a_i \times M_i \times M_i^{-1} \equiv 0(\mod m_j)$
所以只需要把所有的 $a_i \times M_i \times M_i^{-1}$ 加起来就是答案了

int crt(){
    int M = 1, x, y, ans = 0;
    for(int i = 1; i <= n; i ++) M = M * b[i]; //求M
    for(int i = 1; i <= n; i ++){
        int m = M / b[i]; //即Mi
        exgcd(b[i], m, x, y); //求逆元，求得为y
        ans =(ans + y * m * a[i]) % M;//累加答案
    }
    if(ans < 0) ans += M;//判断一下
    return ans;
}

那对于这题呢？
Ctrl + c + Ctrl + v
直接套板子?

${\color{red} WA \\\\\ on\\\ \# 10}$

${\color{white} WTF??}$

？？？？

注意题目中的一句话

所有数据中，第一组数字的绝对值不超过 $10^9$（可能为负数），第二组数字均为不超过 $6000$的正整数，且第二组里所有数的乘积不超过 $10^{18}$

$10^{18}$ ??!! 乘起来不就 $10^{36}$ 爆long long辣

那怎么办
于是就翻题解学习了一个叫做快速乘的东西。。
快速乘就是用来处理在爆long long 的边缘来回试探 的乘法下要取模的一种骚操作
其实应该叫做龟速乘
核心思想就是把一个数按二进制拆分，然后一位一位对应乘。
看代码感性理解一下吧：

int ksc(int a, int b, int mod){
	int ans = 0;
	for(;b; b >>= 1, a = (a + a) % mod) if(b&1) ans = (ans + a) % mod;
	//解释一下, 是把 b 按二进制位拆分， a = a + a 就是每次将 a 乘 2（b每次除2， a肯定要对应乘2嘛）
	//如果b当前位为1，就对答案有贡献
	return ans;
}

然后这题就解决了

${\color{red} 吗？}$

${\color{blue} TLE \\\\\ on\\\ \# 2}$

${\color{white} WTF???}$

哦，忘记说了，由于出题人太毒瘤 输入的 $a_i$可能为负数，所以在做快速乘之前要把它转为正数

没了？
没了。
等等忘记贴代码了：

#include<bits/stdc++.h>
#define int long long
using namespace std;
int exgcd(int a, int b, int &x, int &y){//扩欧 
	if(!b) {x = 1, y = 0; return a;}
	int d = exgcd(b, a % b, x, y);
	int t = x;
	x = y;
	y = t - a / b * y;
	return d;
}
int ksc(int a, int b, int mod){//快速乘 
	int ans = 0;
	for(;b; b >>= 1, a = (a + a) % mod) if(b&1) ans = (ans + a) % mod;
	return ans;
}
int a[15], b[15], n;
int crt(){
	int M = 1, x, y, ans = 0;
	for(int i = 1; i <= n; i ++) M = M * b[i];//算 M 
	for(int i = 1; i <= n; i ++){
		int m = M / b[i];
		exgcd(b[i], m, x, y);//求逆元 
		y = (y % b[i] + b[i]) % b[i];
		ans =(ans + ksc(y, ksc(m, (a[i] + M) % M, M), M) + M) % M;//快速乘，记得a[i]要转为正数 
	}
	if(ans < 0) ans += M;
	return ans;
}
 main(){
	scanf("%lld", &n);
	for(int i = 1; i <= n; i ++) scanf("%lld", &a[i]);
	for(int i = 1; i <= n; i ++) scanf("%lld", &b[i]);
	printf("%lld", crt());
	return 0;
}

貌似龟速 快速乘是可以做到接近O(1)的

#include<bits/stdc++.h>
#define int long long
using namespace std;
int exgcd(int a, int b, int &x, int &y){
    if(!b) {x = 1, y = 0; return a;}
    int d = exgcd(b, a % b, x, y);
    int t = x;
    x = y;
    y = t - a / b * y;
    return d;
}
int ksc(int a, int b, int mod){//开挂般的接近O(1)的快速乘
    a = (a % mod + mod) % mod, b = (b % mod + mod) % mod;
    return ((a * b - (int)((long double)a / mod * b + 1e-6) * mod) % mod + mod) % mod;
}
int a[15], b[15], n;
int crt(){
    int M = 1, x, y, ans = 0;
    for(int i = 1; i <= n; i ++) M = M * b[i];
    for(int i = 1; i <= n; i ++){
        int m = M / b[i];
        exgcd(b[i], m, x, y);
        y = (y % b[i] + b[i]) % b[i];
        ans =(ans + ksc(y, ksc(m, (a[i] + M) % M, M), M) + M) % M;
    }
    if(ans < 0) ans += M;
    return ans;
}
 main(){
    scanf("%lld", &n);
    for(int i = 1; i <= n; i ++) scanf("%lld", &a[i]);
    for(int i = 1; i <= n; i ++) scanf("%lld", &b[i]);
    printf("%lld", crt());
    return 0;
}

${\color{white} 还不够啊!!}$

我是不会告诉你们空白的地方还有字的