1.数学基础
Θ,读音:theta、西塔;既是上界也是下界(tight),等于的意思。
Ο,读音:big-oh、欧米可荣(大写);表示上界(tightness unknown),小于等于的意思。
ο,读音:small-oh、欧米可荣(小写);表示上界(not tight),小于的意思。
Ω,读音:big omega、欧米伽(大写);表示下界(tightness unknown),大于等于的意思。
ω,读音:small omega、欧米伽(小写);表示下界(not tight),大于的意思。
定义:

这里比较的是函数的相对增长率。
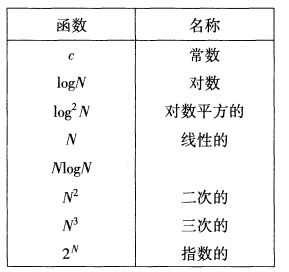
2.模型
为了在正式架构中分析算法,我们需要一个计算模型。我们假设在计算机中所有指令程序都是被顺序的执行,且每一个执行都刚好花费一个时间单位(加法、乘法、赋值等)。
3.要分析的问题
算法要分析的最重要资源就是运行时间,运行时间是衡量一个算法优劣的有效方式。
4.运行时间计算
我们通过一个简单的例子说明分析算法运行时间表示
4.1.实例


其中
17行:1个时间单元(赋值)
18行:2n+1个时间单元(一个赋值,n次表,n次自增)
19行:4n个时间单元(2n次乘法,n次加法,n次赋值)
20行:1个时间单元
总时间单元6n+3,所以我们说该算法是O(N)。
4.2.法则
for循环
一个for循环的运行时间至多是该for循环内部运行语句的时间乘以迭代次数。
嵌套for循环
在一组嵌套for循环内部一条语句运行的总时间为该语句的运行时间乘以改组所有for循环大小的成绩。
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
k++;顺序语句
将各个语句运行时间求和。
![]()
for (int i = 0; i < n; i++)
k++;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
k++;if/else语句

分析算法运行时间的基本策略就是从内部或最深层的部分向外界展开工作。如果有方法调用,那么要先分析这些调用。如果有递归调用,那么有几种选择。
第一种:递归只是被面纱遮住的for循环,其运行时间通常都是O(N):
public static int factorial(int n) {
if (n <= 1) {
return 1;
} else {
return n * factorial(n - 1);
}
}本质上就是一个循环
int n = 1;
for (int i = 1; i <= 5; i++) {
n *= i;
}第二种:当递归被正常使用时,将其转换成循环是相当困难的。
public static int fib(int n) {
1 if (n <= 1)
2 return 1;
3 else
4 return fib(n - 1) + fib(n - 1);
}分析起来是十分简单的,令T(N)为调用fib(n)的运行时间。如果N=0或N=1则运行时间T(N)为常数T(0)=T(1)=1。当N>2时,运行时间为第1行运行时间加上第4行运行时间。有T(N)为fib(n)运行时间则T(N-1)为fib(n-1)运行时间。得出N>2时运行时间公式:T(N) = T(N-1)+T(N-1)+2
由前面我们证明过的斐波那契数列可得
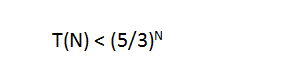
从而得知这个程序的运行时间以指数速度增长。
这个程序之所以运行慢,是由于做了大量重复工作,如在程序第4行计算f(n-1)和f(n-2)的值,其实在f(n-1)函数内部又会重新计算f(n-2)和f(n-3)的值,这样就导致f(n-2)进行了重复计算。所以可以使用一个数组来保存中间计算的值。省去这部分计算。以后会对该递归进行优化。
5.最大子序列问题
问题:给定一个数列,其中可能有正数也可能有负数,我们的任务是找出其中连续的一个子数列(不允许空序列),使它们的和尽可能大。
我们通过4种算法求解来比较不同算法的优劣。
第一种:穷举所有子序列的可能,时间复杂度为
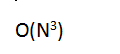
public static int maxSubSum1(int[] a) {
int maxSum = 0;
for (int i = 0; i < a.length; i++) {
for (int j = i; j < a.length; j++) {
int thisSum = 0;
for (int k = i; k < j; k++) {
thisSum += a[k];
}
if (thisSum > maxSum) {
maxSum = thisSum;
}
}
}
return maxSum;
}第二种:经过改良版时间复杂度

public static int maxSubSum2(int[] a) {
int maxSum = 0;
for (int i = 0; i < a.length; i++) {
int thisSum = 0;
for (int j = i; j < a.length; j++) {
thisSum += a[j];
if (thisSum > maxSum) {
maxSum = thisSum;
}
}
}
return maxSum;
}第三种:该方法采用“分治”策略,将系列分为两部分,前半部分与后半部分,分析最大子序列出现的可能性就又三种,第一种出现在前半部分,第二种出现在后半部分,还有一种就是横跨前半部分和后半部分。

public static int maxSubSumRec(int[] a, int left, int right) {
if (left == right) { //基准情况
if (a[left] > 0) {
return a[left];
} else {
return 0;
}
}
int center = (left + right)/2;
int maxLeftSum = maxSubSumRec(a, left, center);
int maxRightSum = maxSubSumRec(a, center, right);
int maxLeftBorderSum=0,leftBorderSum=0;
for(int i=center;i>=left;i--) { //从中间向左遍历
leftBorderSum += a[i];
if(leftBorderSum>maxLeftBorderSum) {
maxLeftBorderSum = leftBorderSum;
}
}
int maxRightBorderSum=0,rightBorderSum=0;
for(int i=center;i<right;i++) { //从中间向右遍历
rightBorderSum += a[i];
if(rightBorderSum>maxRightBorderSum) {
maxRightBorderSum = rightBorderSum;
}
}
//求最大值
return max(maxLeftSum, maxRightSum,maxLeftBorderSum+maxRightBorderSum);
}
设执行该方法的时间为T(N);
方法前面部分执行判断,时间为常量。
中间部分执行两个递归调用,每个递归执行N的一般的计算执行时间为T(N/2)。
再后面两个循环,一共遍历N数量,执行时间为O(N)。
则得到方程组:T(1) = 1 和 T(N) = 2T(N/2) + O(N)

![]()
这个分析的假设是N为2的幂时成立。
第四种:这个算法是聪明的,正确性不那么容易看出来。
public static int maxSubSum4(int[] a ) {
int maxSum = 0, thisSum = 0;
for(int i=0;i<a.length;i++) {
thisSum += a[i];
if(thisSum > maxSum) {
maxSum = thisSum;
}else if(thisSum <0){
thisSum = 0;
}
}
return maxSum;
}比较其中的每一个子序列和,当子序列和为负数时初始化为0重新计算。
6.运行时间中对数
分析算法运行时间最混乱的方面大概就是对数问题。我们已经看到分治算法将以对数时间运行O(N log N)。
此外还有可能出现对数的情况:当通过常数时间的计算可以将问题大小缩减为其一部分(通常1/2),那么该算法就是O(log N)。
下面具体举例三种时间复杂度为对数的情况。
折半查找
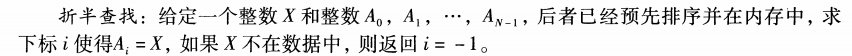
算法实现策略:我们可以通过验证X是否是剧中元素,如果是则找到;如果X小于剧中元素因为系列已经排序,我们可以通过相同的方式验证左侧系列;如果X大于剧中元素则同样的方式验证右侧系列。
public static int binarySearch(int[] a,int x) {
int low =0, high = a.length-1;
while(low <= high) {
int mid = (low + high)/2;
if(a[mid] < x) {
low = mid+1;
}else if(a[mid] > x) {
high = mid -1;
}else {
return a[mid];
}
}
return -1;
}欧里几德算法
第二个例子是计算最大公因数的欧里几德算法。两个整数的最大公因数(gcd)是同时整除二者的最大整数。
定理:两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数。
public static long gcd(long m,long n) {
while(n != 0) {
long rem = m % n; //算法中首先m要大於n,然後求余数,将较小的替换为大数,余数替换为小数。知道余数为0为止。
m = n;
n = rem;
}
return m;
} 幂运算
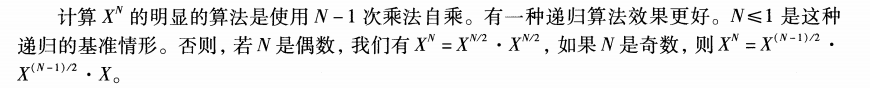

注意:该递归的推进的原则就是n逐渐减小,向n=1或n=0推进。
//求解x的n次幂
public static long pow(long x,int n) {
if(n == 0) {
return 1;
}
if(n == 1) {
return x;
}
if(isEven(n)) {//n为偶数时
return pow(x*x,n/2); //该递归推进的原则就是n中间减小,向0或1基准情形靠近
}else {
return pow(x*x,n/2)*x;
}
}转载于:https://my.oschina.net/u/3100849/blog/3057469
