渐进记号
\(O\)渐进上界,\(\Theta\)渐进紧确界,\(\Omega\)渐进下界,\(o\)非渐进紧确上界,\(\omega\)非渐进紧确下界
例如\(2n^2 = O(n^2)\)是渐进紧确的,但\(2n = O(n^2)\)不是渐进紧确的,我们使用\(2n = o(n^2)\)
公式
\(\lg(n!) = \Theta(nlgn)\)
\(a^{\log_b{n}} = n ^ {\log_b{a}}\)
主定理
假设有递归式
\(T(n) = aT(\frac{n}{b}) + f(n), a \geq 1, b \gt 1\)
情况一
若\(f(n) = O(n^{\log_b{a} - \epsilon}), \epsilon > 0\)
则\(T(n) = \Theta(n^{\log_b{a}})\)
如\(T(n) = 9T(\frac{n}{3}) + n\), \(T(n) = \Theta(n^2)\)
情况二
若\(f(n) = \Theta(n^{\log_b{a}})\)
则\(T(n) = \Theta(n^{\log_b{a}} \log_2{n})\)
如\(T(n) = T(\frac{2n}{3}) + 1\), \(T(n) = \Theta(\log_2{n})\)
情况三
若\(f(n) = \Omega(n^{\log_b{a} + \epsilon}), \epsilon > 0\)且对于某个常数\(c<1\)和足够大的\(n\)有\(af(\frac{n}{b}) \leq cf(n)\)
则\(T(n) = \Theta(f(n))\)
如\(T(n) = 3T(\frac{n}{4}) + n\log_2{n}\), \(T(n) = \Theta(n\log_2{n})\)
例子
对于\(T(n) = 2T(\frac{n}{2}) + n\log_2{n}\),不能应用情况三,因为\(\frac{f(n)}{n} = \log_2{n}\)都渐进小于\(n^\epsilon\)
证明主定理
画递归树
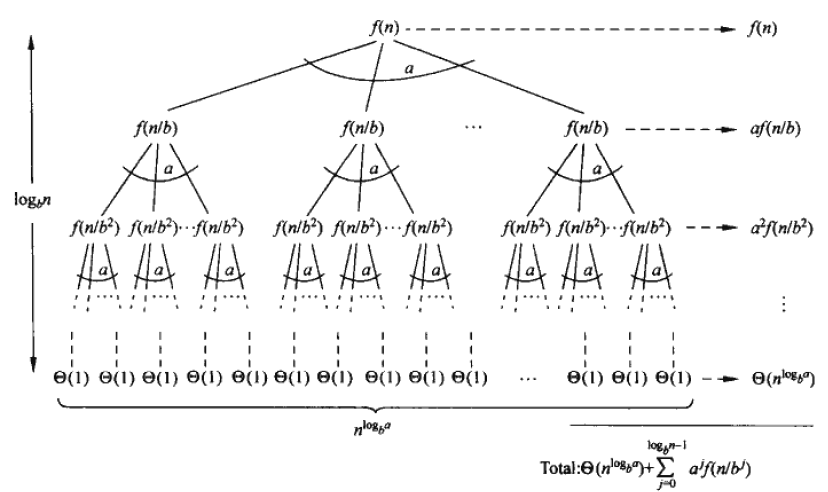
现在只需要计算
\[ g(n) = \sum_{j=0}^{\log_b{n} - 1} a^j f(\frac{n}{b^j}) \]
带入即可证明
练习
若\(f(n) = \Theta(n^{\log_b{a}}\lg^k n), k \ge 0\)
则\(T(n) = \Theta(n^{\log_b{a}}\lg^{k+1} n)\), 简单起见假定\(n\)是\(b\)的幂