参考博客有：https://blog.csdn.net/WMN7Q/article/details/70174300
一、时间序列的概念
按时间顺序排列的n个随机变量X1,X2,…,Xn称为随机变量X的时间序列，简记为{Xn}，而x1,x2,…,xn代表随机变量X的时间序列的n个有序观察值。
比如某饭店在1月1号到1月10号所有菜品的日销量数据如下图所示：
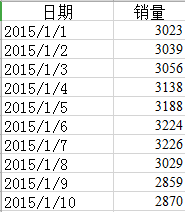则称3023,3039,3056,3138,3188,3224,3226,3029,2859,2870为销量这一随机变量的时间序列的10个有序观察值。
二、时间序列的预处理
在拿到随机变量的时间序列对应的观察值序列后，首先要检验观察值序列的平稳性和纯随机性。
平稳性检验：
(1)时序图法
平稳时间序列的均值和方差都为常数，所以平稳时间序列的时序图应该呈现出序列值(观察值)在某一常数附近随机波动，而且波动的范围有限。如果时序图有明显的趋势性或周期性，则不是平稳序列。
例：对某饭店1月份和2月份所有菜品的日销量数据绘制时序图
部分数据展示如下：
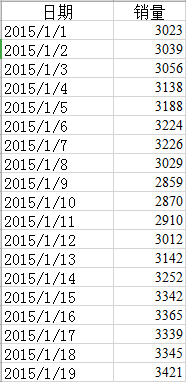
时序图：
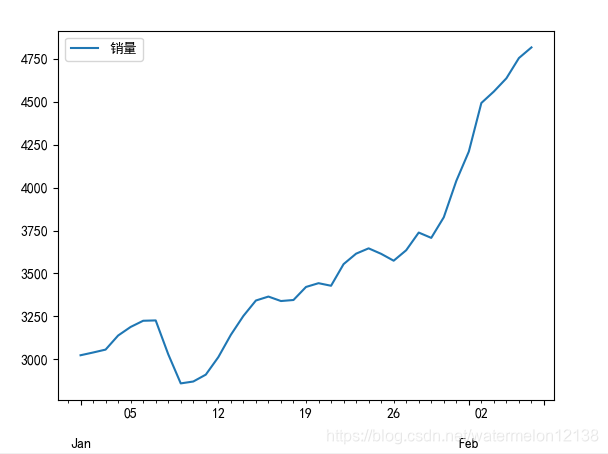
可见销量随着天数处于增长趋势，所以销量的时间序列不是平稳序列。
(2)自相关系数图法
平稳序列具有短期相关性，也就是对于平稳序列而言只有近期的序列值会对当前序列值产生的影响比较明显，间隔越远的序列值对当前值的影响越小。所以随着延迟(滞后)期数k的增加，平稳序列的自相关系数ρk会较快的衰减趋向于零，并在零附近波动。而非平稳序列的自相关系数则衰减的比较缓慢。
自相关系数：
为什么叫自相关系数，简单来说因为计算该相关系数的值都来自同一个变量。因为它是用来衡量同一个随机变量在两个不同时间段内的观察值的相关程度，也就是衡量自己过去的行为对现在造成影响。
假设某一随机变量X的时间序列的观察值序列如下：
x1,x2,x3,x4,x5,x6,x7,x8,x9,x10
延迟或滞后3期将观察值序列分为两组：
(x1滞后3期为x4，以此类推)
第一组：x1,x2,x3,x4,x5,x6,x7
第二组：x4,x5,x6,x7,x8,x9,x10
所以滞后3期得到随机变量X的时间序列的自相关系数ρ3为：
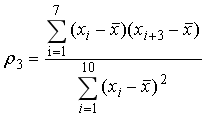
经扩展可得任一随机变量X的时间序列滞后k期的自相关系数ρk:
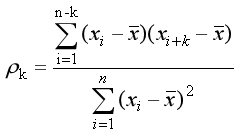
偏自相关系数：
计算一个随机变量X的时间序列滞后k期的自相关系数ρk，实际上我们得到是
x1,x2,…xn-k和xk+1,xk+2,…,xn的相关关系，并没有直接衡量x1与xk+1，x2与xk+2，…，xn-k与xn之间的相关关系。对于xn-k与xn来说，滞后k期的自相关系数ρk里面掺杂了xn-k到xn之间的k-1个值对xn的影响，而偏自相关系数就是用来衡量xn-k和xn之间的直接相关关系。
公式如下：
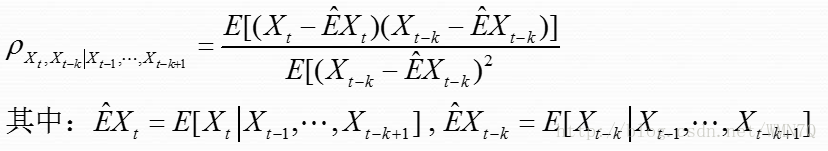
上式中E^Xt = E [Xt,Xt-k | Xt-1,…,Xt-k+1]指的是在剔除了Xt-1,…,Xt-k+1的干扰后求得的期望，那么ρ Xt,Xt-k | Xt-1,…,Xt-k+1指的就是在剔除了Xt-1,…,Xt-k+1的干扰后求得的相关系数。可见这只是一种理想的状况，在实际情况中剔除k-1个变量的干扰非常不易。
但是可以利用Yule-Walker方程式求解偏自相关系数，求解方法见下面的博客：
https://blog.csdn.net/WMN7Q/article/details/70174300
知道了什么是自相关系数，接下来就可以绘制一个随机变量X的时间序列的自相关系数图，数据还是用上文中提到的销量数据。
自相关系数图如下：
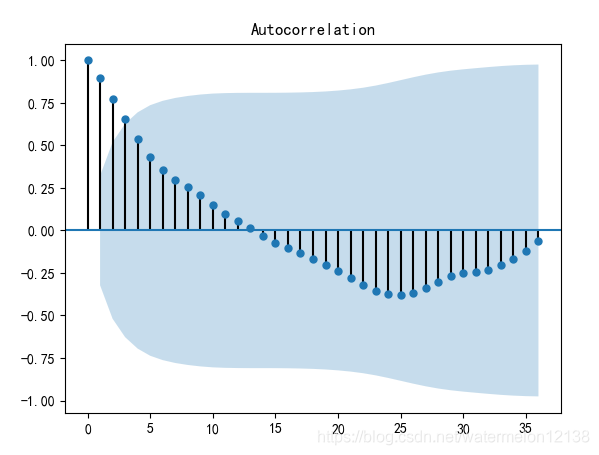
由上图可知销量的时间序列的自相关系数长期不为0，也就是该序列存在长期相关性，并且衰减速度缓慢，所以该序列是不平稳序列。
(3)单位根检验
单位根检验是指检验序列中是否存在单位根，如果存在单位根该序列就是不平稳时间序列。
# 平稳性检验(单位根检验)
# 若pvalue大于显著水平(一般为0.05)则拒绝原假设，认为它是不平稳的
# from statsmodels.tsa.stattools import adfuller as ADF
# print(u'时间序列的ADF检验结果为：', ADF(时间序列))
# 返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
纯随机性检验(白噪声检验)
如果一个序列是纯随机性序列，那么该序列的序列值之间应没有任何关系，也就是该序列任一滞后期的自相关系数都为0。但在实际情况中它们并不等于0，只是接近0并在0的周围波动。
一般是构造检验统计量来检验序列的纯随机性，常用的统计量有Q统计量和LB统计量。
# 白噪声检验
# 若pvalue大于显著水平(0.05)则认为它是白噪声序列(或纯随机性序列)
from statsmodels.stats.diagnostic import acorr_ljungbox
# Ljung-Box test for no autocorrelation，Ljung-Box是进行无自相关性的检验(也称之为纯随机性检验和白噪声检验)
# 检验某时间序列在滞后1期时是否是白噪声()
# print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(时间序列, lags=1)) # 返回统计量和p值
三、时间序列分析
1.如果时间序列是白噪声序列则放弃分析。
2.如果序列是平稳非白噪声序列，则可用AR模型、MA模型或ARMA模型来进行序列分析。
AR模型(Autoregressive Model)：
具有如下结构的模型称为p阶自回归模型，简记为AR（p）。
其中Xt是随机变量在 t 时刻的取值，AR模型认为该取值和它前p期的取值Xt-1,Xt-2,…,Xt-p有关，所以要建立它们之间的多元线性回归。误差项εt是当前t时刻的随机干扰，属于零均值白噪声序列。
由AR模型的公式可以推出以下信息：
- 均值
所以能够使用AR模型的时间序列的均值必须是常数，既然满足了平稳性，那该时间序列的均值肯定是常数。 - 方差
对模型方程两边同时求方差，则可得能够使用AR模型的时间序列的方差必须也是常数。 - 自相关系数
能够使用AR模型的时间序列要求它的自相关性系数呈指数衰减，并且始终有非零取值，不会出现当滞后期k取大于某个常数时它的自相关性为零，也就是说能够使用AR模型的时间序列要求它的自相关性系数ρk满足拖尾性(接近0但就是不为0)。 - 偏自相关系数
能够使用AR模型的时间序列要求它的偏自相关性系数满足截尾性(一下就为0了)。
总结：能够使用AR模型的时间序列应该满足如下性质
MA模型(Moving Average Model)
MA模型也称滑动平均模型，具有如下结构的就称为q阶滑动平均模型，简记为MA(q)。
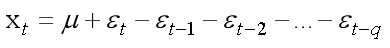
其中Xt是随机变量在 t 时刻的取值，μ为随机变量均值，εt为当前时刻的随机扰动属于零均值白噪声序列。该模型认为随机变量在 t 时刻和前q期的随机扰动有关，所以建立它们的多元线性回归。
总结：能够使用MA模型的时间序列应该满足如下性质
ARMA模型(Autoregressive Moving Average Model)
具有如下结构的模型称为自回归移动平均模型，简记为ARMA(p,q)。
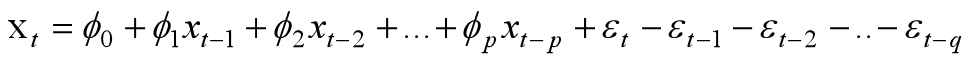
可见ARMA模型认为当前时刻t的取值与前p期的取值和前q期的随机扰动有关。特别的，当q=0时ARMA模型等于AR模型，当p=0时ARMA模型等于MA模型。
总结：能够使用ARMA模型的时间序列应该满足如下性质
平稳非白噪声序列选择模型的步骤：
(1)计算时间序列的自相关系数(ACF)和偏自相关系数(PACF)
(2)模型定阶。根据AR模型、MA模型和ARMA模型的自相关性系数和偏自相关性系数的性质选择适合该时间序列的模型。
3.如果时间序列是非平稳序列，则可以选择ARIMA模型进行分析。
ARIMA模型
差分运算：
一阶差分运算为相距一期的两个序列值之间的减法运算。
同理k阶差分运算为相距k期的两个序列值之间的减法运算。
(Series格式和DataFrame格式的数据可直接调用diff()求差分序列)
# df为dataframe格式
>>> df
a b c
0 1 1 1
1 2 1 4
2 3 2 9
3 4 3 16
4 5 5 25
5 6 8 36
# periods默认为1，代表1阶差分运算
>>> df.diff()
a b c
0 NaN NaN NaN
1 1.0 0.0 3.0
2 1.0 1.0 5.0
3 1.0 1.0 7.0
4 1.0 2.0 9.0
5 1.0 3.0 11.0
# periods=3，代表3阶差分运算
>>> df.diff(periods=3)
a b c
0 NaN NaN NaN
1 NaN NaN NaN
2 NaN NaN NaN
3 3.0 2.0 15.0
4 3.0 4.0 21.0
5 3.0 6.0 27.0
ARIMA模型的实质是差分运算和ARMA模型的结合，因为许多非平稳序列差分后变为平稳序列。当某个时间序列是非平稳序列，我们求它的k阶平稳序列(k从1开始取)，这样得到的平稳序列也叫差分平稳序列，对差分平稳序列可以使用ARMA模型进行拟合。
差分平稳序列的建模步骤如下：
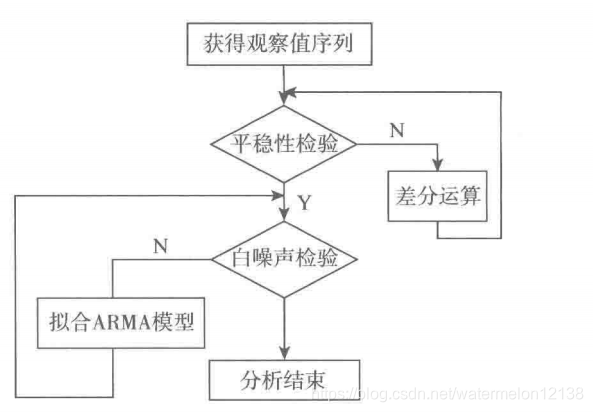
例子：对菜品日销量的时间序列进行建模，并预测未来几天内菜品的日销量数据
部分数据展示如下：
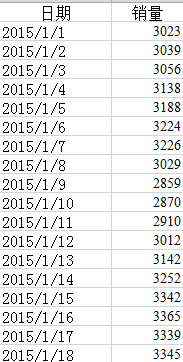
(1)检验该序列的平稳性
时序图如下：
自相关系数图如下：
单位根检验如下：
从上图可以看出，该序列有明显的递增趋势，并且有长期的相关性，单位根检验统计量的p值大于0.05，最终判定该序列为非平稳序列。
(2)差分运算。
对上面的非平稳序列进行k阶差分，对差分后的序列再次进行平稳性检验。
从一阶差分开始，接下来对一阶差分后的序列进行平稳性检验：
时序图如下：
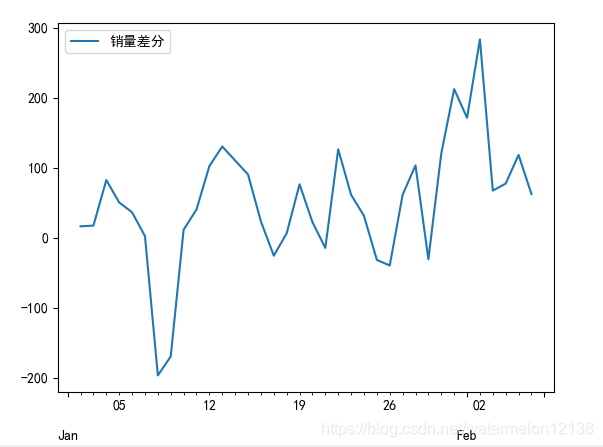
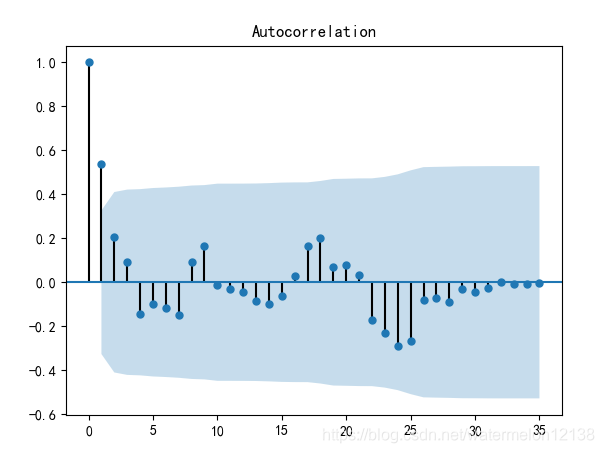
自相关系数图如下：
单位根检验：
从上图可以看出，经过一阶差分后的序列的取值围绕某一常数上下波动，大部分自相关系数都为0，可见它有短期相关性，并且单位根检验p值小于0.05，最终判定一阶差分后的序列为平稳序列，那就不用再继续进行差分运算了。
(3)白噪声检验
使用LB(Ljung-Box )统计量来检验一阶差分后的序列是否为白噪声序列。
检验结果如下：
可见一阶差分后的序列是非白噪声序列。
(4)模型定阶(确定ARMA模型的p和q)
方法一：人为识别
一阶差分后的序列的偏自相关系数图如下：
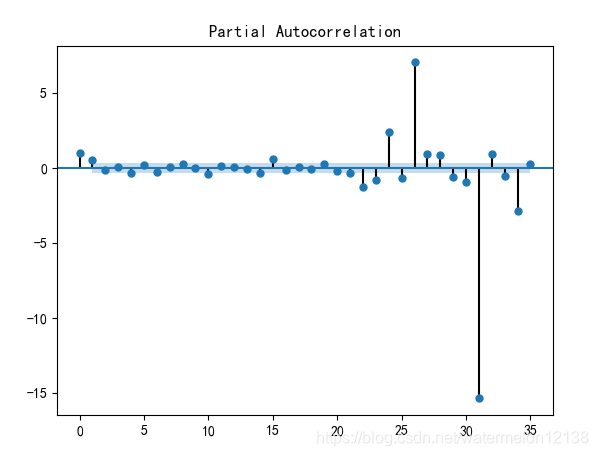
可见一阶差分后的序列的自相关系数图显示出截尾，而偏自相关系数图显示出拖尾(0的周围上下波动，就是不为0)，所以根据AR模型、MA模型和ARMA模型的性质我们应该选择MA模型，即确定p=0，q=1。
方法二：
取p，q都小于等于3的所有组合计算BIC信息量，取BIC信息量达到最小的那一对组合。
计算出的BIC矩阵如下：
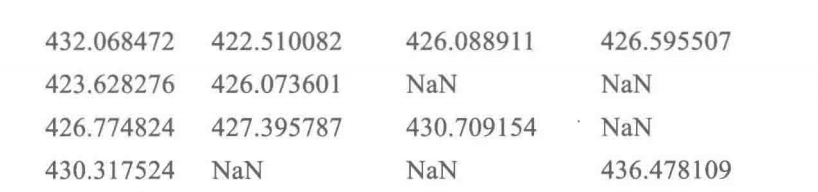
可见BIC的最小值为422.520082，此时p=0，q=1。
(5)建立ARIMA(0,1,1)并进行预测
# -*- coding: utf-8 -*-
# arima时序模型
import pandas as pd
# 参数初始化
path = 'F:/DataMining/chapter5/arima_data.xls'
forecastnum = 5
# 读取数据，指定日期列为指标，Pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel(path, index_col=u'日期')
# print('data: \n', data)
# # 时序图
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# data.plot()
# plt.show()
# 自相关图
# from statsmodels.graphics.tsaplots import plot_acf
# plot_acf(data)
# plt.show()
# 平稳性检验(单位根检验)
# 若pvalue大于显著水平(一般为0.05)则拒绝原假设，认为它是不平稳的
# from statsmodels.tsa.stattools import adfuller as ADF
# # print('data[销量]: \n', data['销量'])
# print(u'原始序列的ADF检验结果为：', ADF(data[u'销量']))
# 返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore
# # 差分后的结果
# diff()为pandas中计算差分的函数，默认为1阶差分
# dropna()为去掉结果中的NAN
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
# print('D_data: \n', D_data)
# D_data.plot() # 时序图
# from statsmodels.graphics.tsaplots import plot_acf
# plot_acf(D_data) # 自相关图
# from statsmodels.graphics.tsaplots import plot_pacf
# plot_pacf(D_data) # 偏自相关图
# from statsmodels.tsa.stattools import adfuller as ADF
# print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分'])) # 平稳性检测
# plt.show()
# 白噪声检验
# 若pvalue大于显著水平(0.05)则认为它是白噪声序列(或纯随机性序列)
# from statsmodels.stats.diagnostic import acorr_ljungbox
# # Ljung-Box test for no autocorrelation，Ljung-Box是进行无自相关性的检验(也称之为纯随机性检验和白噪声检验)
# # 检验D_data在滞后1期时是否是白噪声()
# print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1)) # 返回统计量和p值
from statsmodels.tsa.arima_model import ARIMA
data[u'销量'] = data[u'销量'].astype(float)
# 定阶
pmax = int(len(D_data)/10) # 一般阶数不超过length/10
qmax = int(len(D_data)/10) # 一般阶数不超过length/10
bic_matrix = [] # bic矩阵
for p in range(pmax+1):
tmp = []
for q in range(qmax+1):
try: # 存在部分报错，所以用try来跳过报错。
# order=(p, d, q)，其中p，q为arima模型中的阶数，d代表差分的阶数
# 因为data的一阶差分序列是平稳非白噪声序列，所以这里是对data的一阶差分序列建模即d=1
tmp.append(ARIMA(data, order=(p, 1, q)).fit().bic)
except Exception as e:
print(e)
tmp.append(None)
bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix) # 从中可以找出最小值
print('bic_matrix: \n', bic_matrix)
print('bic_matrix_stack: \n', type(bic_matrix.stack()))
# 以元组形式返回行索引
p, q = bic_matrix.stack().idxmin() # 先用stack展平，然后用idxmin找出最小值位置。
print(u'BIC最小的p值和q值为：%s,%s' % (p, q))
model = ARIMA(data, (p, 1, q)).fit() # 建立ARIMA(0, 1, 1)模型
print('模型报告: \n', model.summary2()) # 给出一份模型报告
# steps=5表示从样本的末尾再往后预测5个
# # model.forecast()依次返回的是(预测值数组,预测值的标准差数组，预测值的置信区间)
print('预测结果: \n', model.forecast(steps=5)) # 作为期5天的预测，返回预测结果、标准误差、置信区间。
进行为期5天的预测结果为：
[4873.9665477 , 4923.92261622, 4973.87868474, 5023.83475326, 5073.79082178]
预测结果仍然处于上升趋势，还是比较靠谱的。
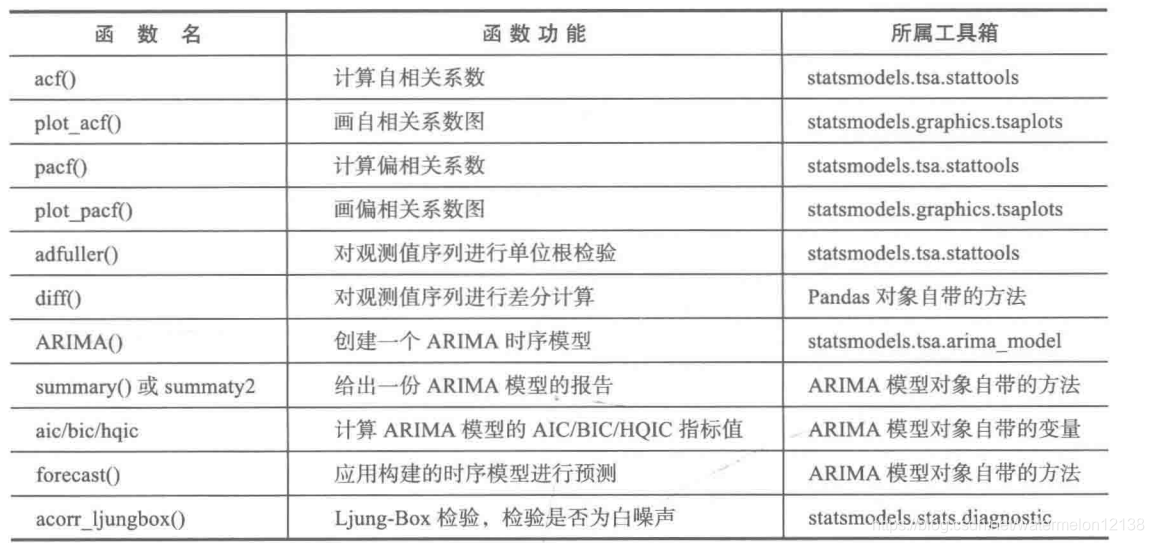
4.时间序列算法中应用到的相关函数
