【数据挖掘】时间序列教程【三】

2.7 平稳性

序列的平稳性 $X_1,X_t \dots$ 是一个关键属性，它允许我们应用许多时间序列分析的标准工具。

如果对于大小 n 和任何整数 $\tau$ ,观察发现 $Y_{t_1} ,Y_{t_2} \dots Y_{t_n }$ 具有与 $Y_{t_1+ \tau} ,Y_{t_2+ \tau} \dots Y_{t_n+ \tau }$ 相同的联合分布，则时间序列是严格平稳的。
换句话说，从分布的角度来看，平稳时间序列对移位是不变的
因为定义适用于所有 n ，包括 n=1 ，所以我们得出 $Y_t$ 的均值和方差对于所有 t 都是常数。

有时严格的平稳性太难要求，所以我们通常使用较弱的概念。

如果均值是常数，并且任意两个值之间的协方差仅取决于这两个值之间的时间差（而不是 \（t\）本身的值），则时间序列是二阶平稳的。
$\mathbb{E}[Y_t] = \mu$ 。
$\text{Cov} (Y_t,Y_{t+\tau}) = \gamma( \tau)$ ，仅 $\tau$ 的函数。

函数 $\gamma()$ 称为自动协方差函数。

在大多数情况下，我们将假设时间序列是二阶平稳的，并且不关心数据联合分布的更高时刻。

平稳性的基本思想是数据的分布不依赖于t，因此了解t本身并不能告诉您有关分布的任何信息。这使我们能够将时间序列视为随时间推移的“稳定”，因此虽然可能会不时出现随机偏差，但随着时间的推移，分布不会发生重大变化。

平稳性可以通过以下方式考虑：想象一下，您此刻正在“查看”您的时间序列。然后我们快进时钟 6 个月，您会看到 6 个月后出现的时间序列。它看起来有根本的不同吗？当然，值会有随机变化，但如果我没有告诉你是 6 个月后，你能说时间已经转移了吗？如果答案为“否”，则时间序列是静止的。

考虑另一个示例：假设您正在跟踪您所在城市的温度时间序列，而此时是冬天。现在，如果我快进 6 个月，情况看起来会大不相同。现在是夏天，温度会暖和很多。很明显，我们穿越了时间。这是一个非平稳时间序列的示例，因为数据的分布取决于时间本身。

现在考虑以下场景：假设您正在查看当前一周城市随时间推移的每小时温度。然后我把你转移到未来一周。每小时温度的时间序列是否与前一周大不相同？可能不是，因为时移相对较小。这表明我们正在考虑的时间尺度变化在我们是否认为时间序列是平稳的方面起着重要作用。将时间序列视为超过 6 个月时移的平稳可能不现实，但将其视为超过 1 周时移的平稳可能更合理。

但平稳性的定义是，该属性应该在所有时间变化中都保持不变。那么，我们能做的什么是实际的事情呢？

考虑下面的图表，它显示了 2005 年马里兰州巴尔的摩市的日平均温度。

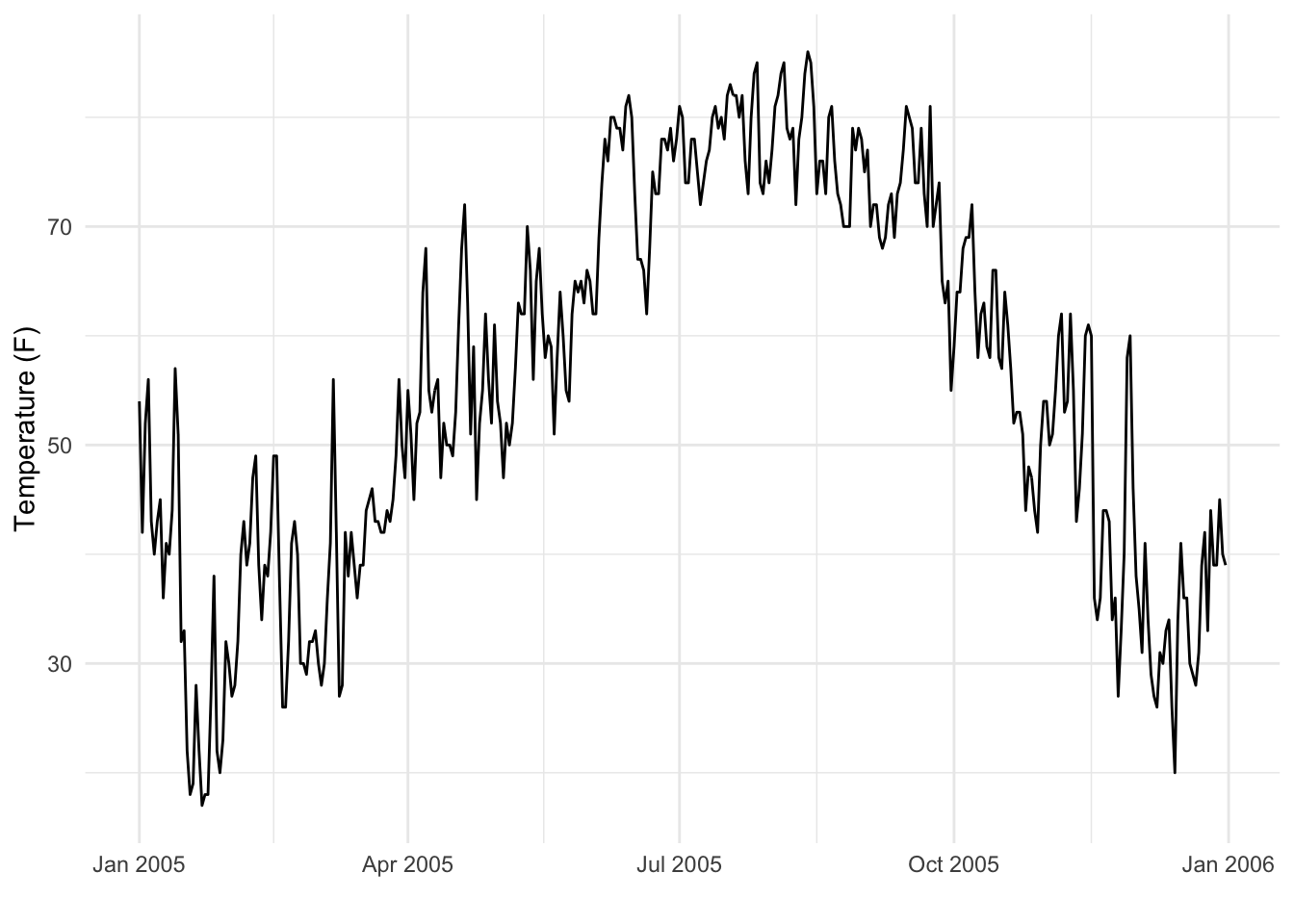
正如人们所预料的那样，有一个强烈的季节性模式，冬季温度较低，夏季温度较高。显然，该序列是非平稳的，因为知道它是 7 月可以为您提供有关温度数据分布的大量信息。

下图显示了拟合具有恒定月效应的线性模型后的残差。

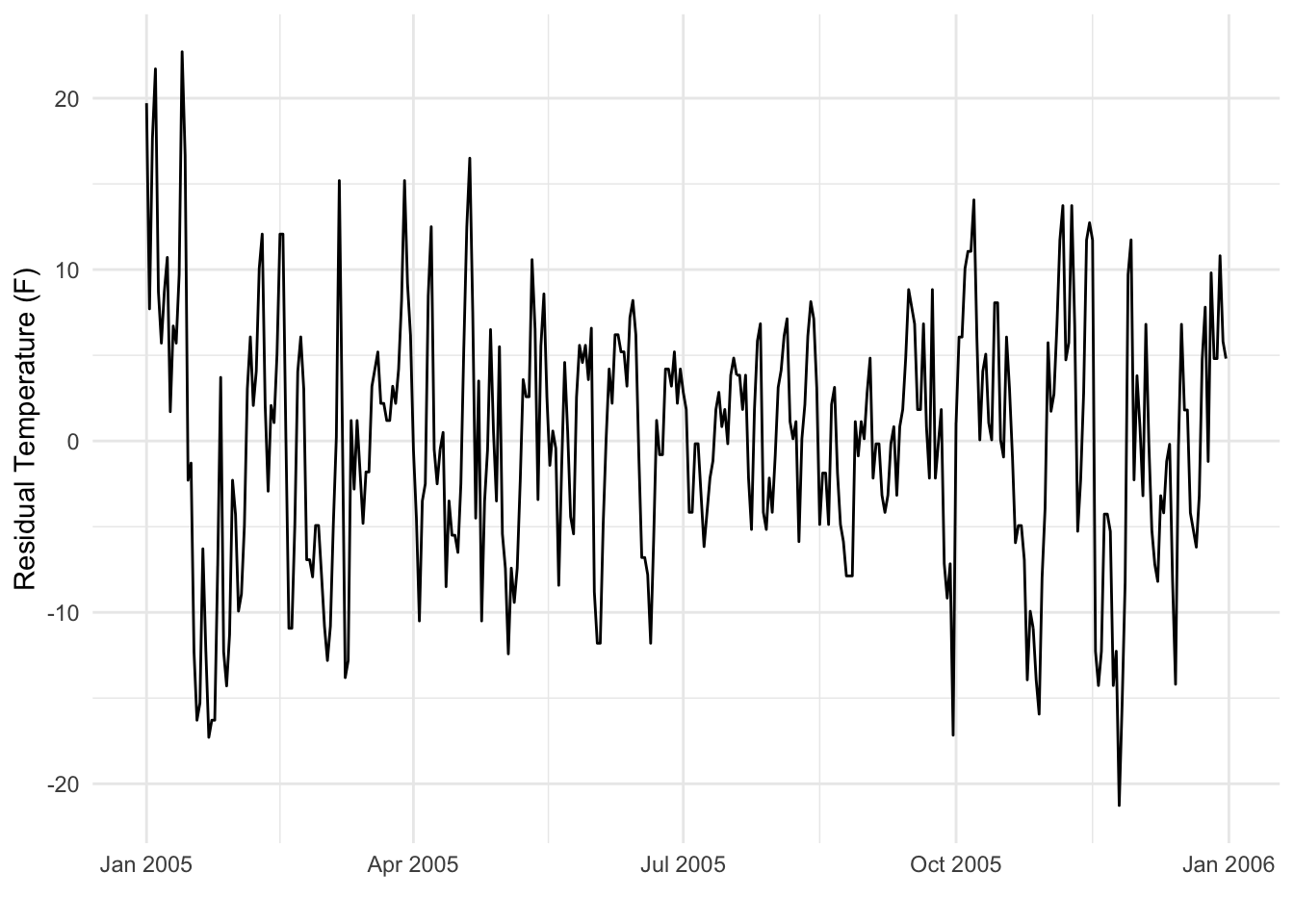
此图确实显示了某种模式，主要是其随时间变化的变异性，但总体均值为零，在拟合线性模型后应该如此。可以合理地认为，这个系列看起来比前一个系列“更稳定”，去除了月度趋势。但是，冬季月份的方差似乎确实大于夏季月份。

这里的底线是温度序列具有很强的固定效应，这是季节性模式。在去除了固定效应之后，我们可以提出一个更好的论证，即残差变化是静止的。在传统的回归设置中，我们可能会假设残差变异是独立且相同分布（iid）的，但在时间序列上下文中，即使序列是平稳的，也可能残留一些残差自相关。

2.8 自相关

平稳时间序列的一个汇总统计量是自相关函数或 ACF。这只是自协方差函数 $\gamma(k)$ 除以 $\gamma(0)$ 。因此，ACF（0）始终为 1，通常我们绘制的图甚至每次都认为它相同。

这是2017-2018年的原始圣路易斯颗粒物数据。

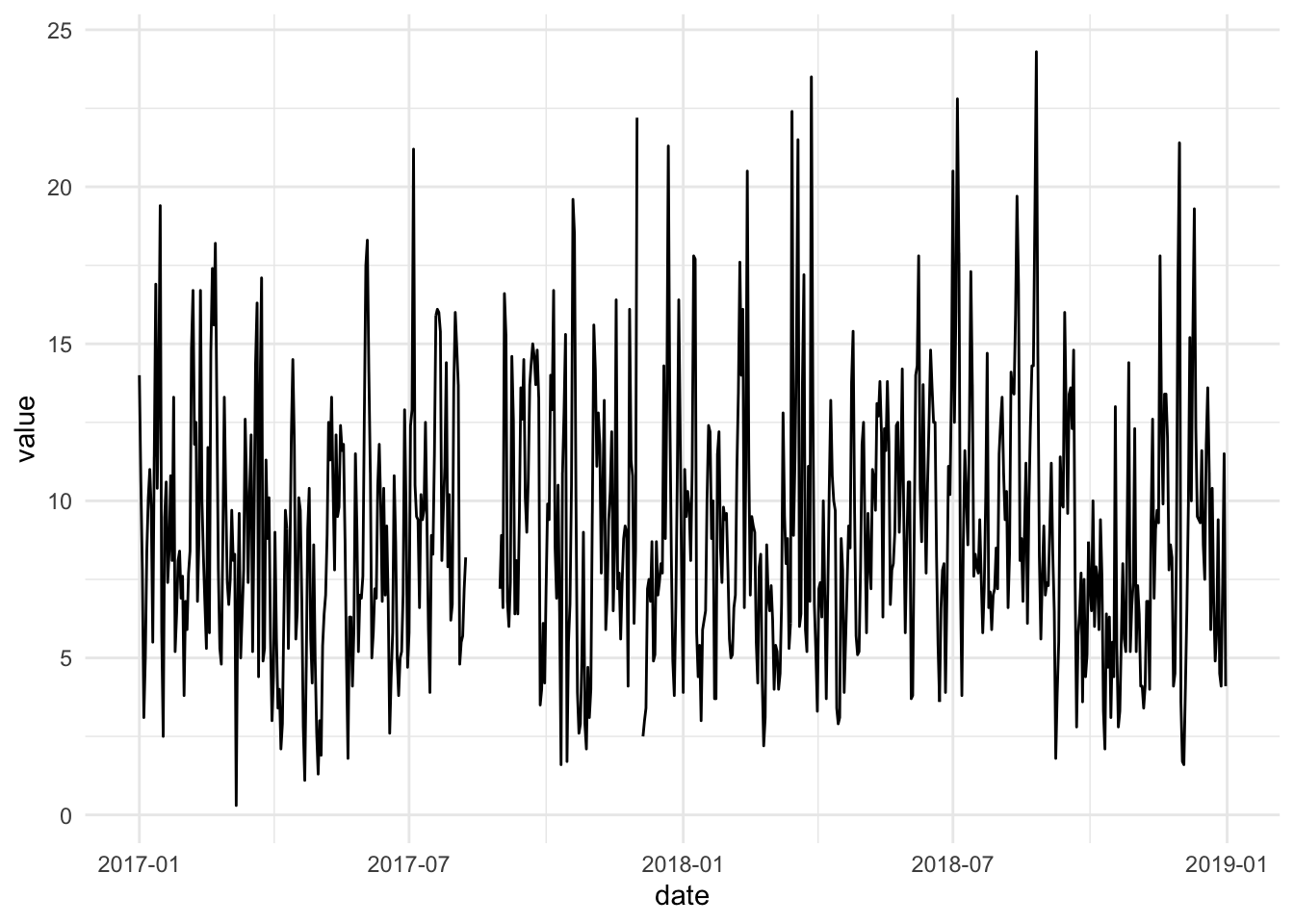
让我们从数据中删除平滑的月平均周期趋势，并查看残差。

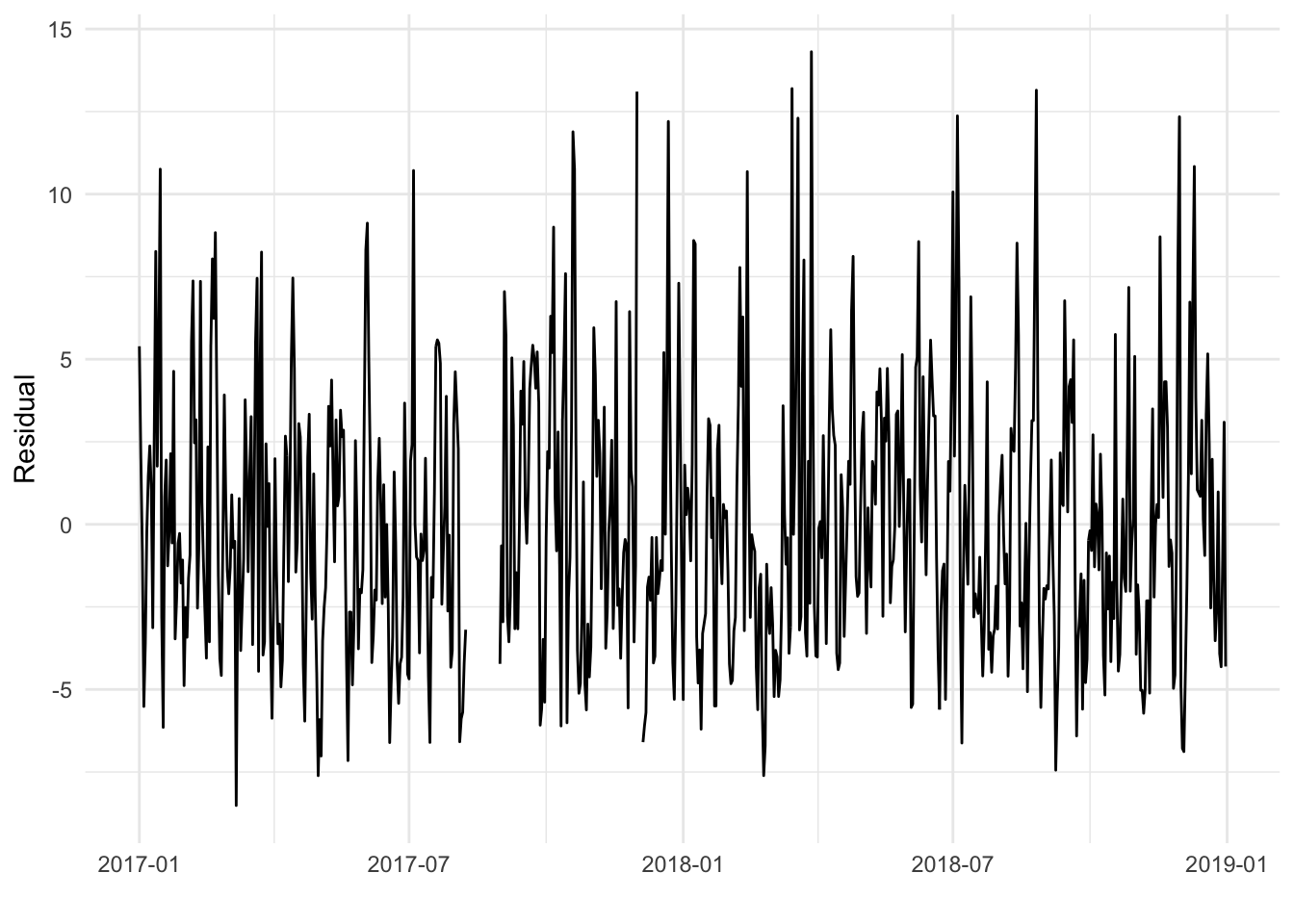
这是去除趋势和月度效应后圣路易斯数据的自相关函数。

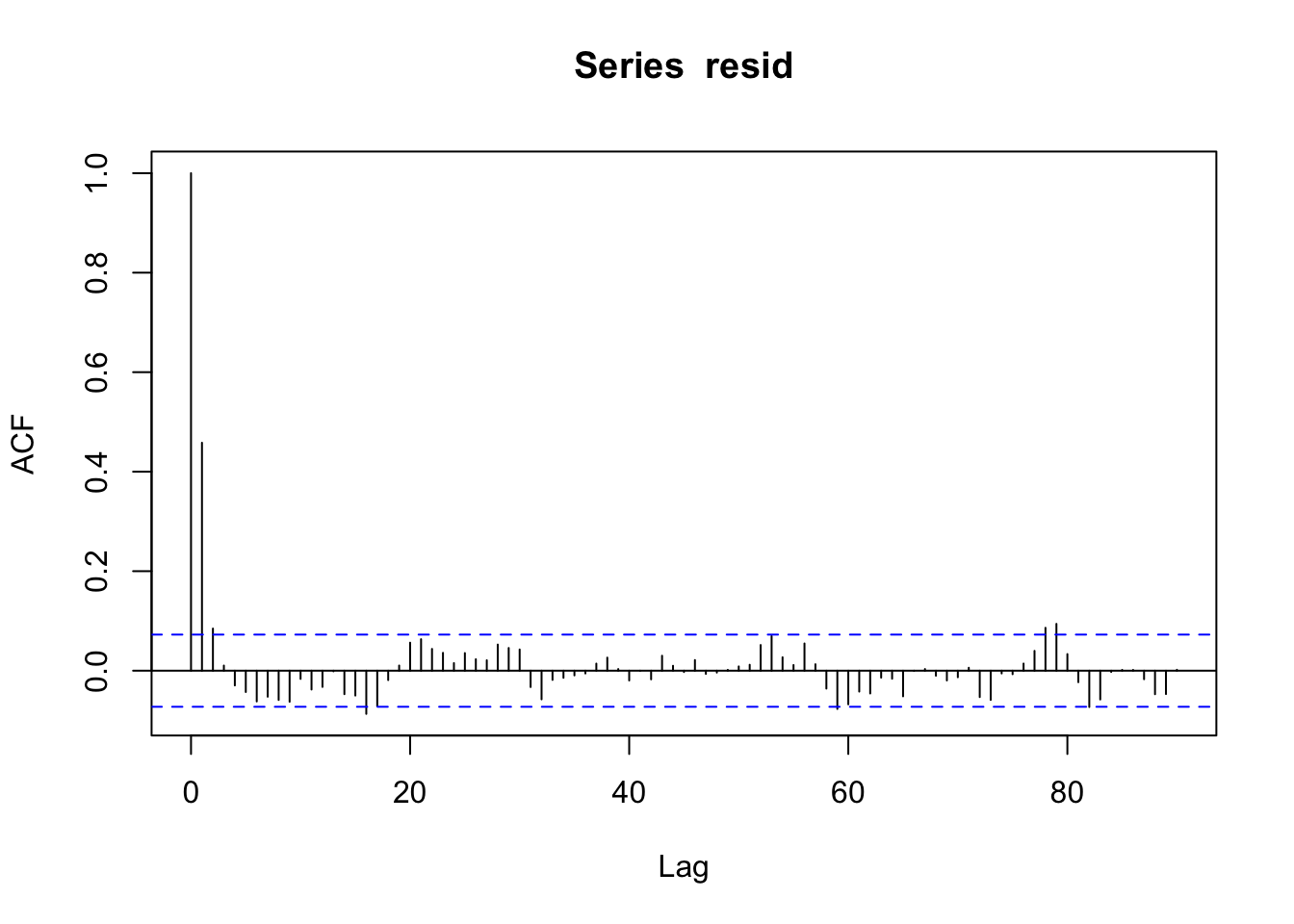
我们可以看到，在滞后 1 天时似乎有一些相关性，但剩余滞后处的相关性接近于零。

与圣路易斯数据相反，这里是弗雷斯诺数据。

您不想看到的是如下所示的内容。这是原始弗雷斯诺数据上的 ACF。

那么这里的问题是，为什么在滞后 1、2、3、...？问题是数据无法回答这个问题。它可能是序列中真正的随机自相关，或者存在尚未删除的固定效应或趋势（即序列不是平稳的）。

ACF 图中的这种模式通常表示非平稳性，而不是有趣的自相关的迹象。如果看到类似这样的内容，则应检查时间序列是否表现出任何强大的固定效应，例如线性趋势或季节性分量。如果是这样，则应首先消除这些效应（例如通过回归建模），并重新绘制ACF图。

作为另一个示例，这是去除月平均值后上一节中显示的巴尔的摩温度数据残差的 ACF 图。

ACF 图清楚地表明残差中还剩下一些短期自相关。如何处理这将取决于手头的应用程序和问题，我们将在时间序列回归建模一节中进一步讨论这个问题。

2.9 高斯过程

我们经常处理高斯时间过程，它们是联合分布为高斯的平稳过程。也就是说，对于序列 $Y_1,\dots,Y_n$ ，它们联合分布为 $\mathcal{N}(\mathbf{1}\mu,\Sigma(\gamma))$ ，其中 $\gamma$ 是自协方差函数，使得 $\gamma(k) = \text{Cov}( Y_j,Y_{j+k} )$ 对于所有整数 j 和 k 。请注意，对于所有 \（j\），我们也有 $\gamma(0) = \text{Cov} (Y_j, Y_j) = \text{Var} (Y_j )$ 。

从柯西-施瓦茨不等式中，我们可以看到:

${Cov}(Y_j,Y_{j+k})^2 \leq {Var}(Y_j) {Var}(Y_{j+k})\\ = \gamma(0)^2\\ Cov (Y_j,Y_{j+k}) \leq \gamma(0)$

在实践中，我们通常假设 $\gamma(k)\rightarrow 0$ 为 $k\rightarrow\infty$ ，因此观测值 $Y_j$ 和 $Y_{j+k}$ 之间的依赖性在一定的滞后距离 $k$ 后衰减。如果是 $k$ 的 $\gamma (k) =0$ 此时 $k> m$ ，则时间序列称为 m-相关序列。