等式约束优化（可行点）

《Convex Optimization》

之前，讲的下降方法以及Newton方法都是在无约束条件的前提下的。这里讨论的是在等式约束（线性方程）的前提下讨论的。我们研究的是下面的凸优化问题：
$\begin{array}{ll} minimize & f(x) \\ s.t. & Ax=b \end{array}$
其中 $f:\mathbb{R}^n \rightarrow \mathbb{R}, A \in \mathbb{R}^{p\times n}, rank A = p<n$
请不要怀疑 $rank A = p<n$条件的可靠性，否则，只需找出其线性无关组即可。而且，显然，如果 $Ax=b$如果无解，那么优化问题同样无解。
通过对对偶问题，及KKT条件的分析，可以知道，该优化问题存在最优解的充要条件是，存在 $v^* \in \mathbb{R}^p$满足：
$Ax^*=b, \quad \nabla f(x^*) + A^Tv^*=0$

策略一 消除等式约束

我们首先确定矩阵 $F \in \mathbb{R}^{n \times (n-p)}$和向量 $\hat{x} \in \mathbb{R}^n$，用以参数化可行集：
$\{x|Ax=b\} = \{Fz+\hat{x}|z \in \mathbb{R}^{n-p} \}$
只需， $\hat{x}$为 $Ax=b$的一个特解即可。 $F$是值域为 $A$的零空间的任何矩阵（满足 $A(Fz)=0$，即 $Fz$可以取得所有 $Ax=0$的解）。于是等式约束问题就可以变为无约束问题：
$minimize \quad \widetilde{f}(z) = f(Fz+\hat{x})$
我们也可以为等式约束构造一个最优的对偶变量 $v^*$:
$v^*=-(AA^T)^{-1}A\nabla f(x^*)$

另外需要注意的是，如果 $F$是一个消除矩阵，那么任意的 $FT$同样也是合适的消除矩阵，其中 $T \in \mathbb{R}^{(n-p) \times (n-p)}$是非奇异的。

策略二 Newton方向

我们希望导出等式约束问题：
$\begin{array}{ll} minimize & f(x) \\ s.t. & Ax=b \end{array}$
在可行点 $x$处䣌Newton方向 $\Delta x_{nt}$，将目标函数换成在x附近的二阶泰勒近似：
$\begin{array}{ll} minimize & \hat{f}(x+v)=f(x)+\nabla f(x)^{T}v + \frac{1}{2}v^T\nabla^2 f(x) v \\ s.t. & A(x+v)=b \end{array}$
注意上述问题时关于 $v$的优化问题。
根据我们在文章开头提到的最优性条件，可以得到：

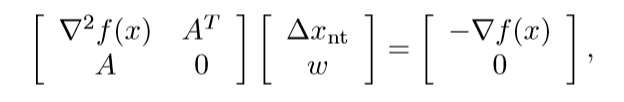
其中 $\Delta x_{nt}$表示Newton方向， $w$是该二次问题的最优对偶变量。

另外一种解释

我们可以将Newton方向 $\Delta x_{nt}$及其相关向量 $w$解释为最优性条件
$Ax^*=b, \quad \nabla f(x^*) + A^Tv^*=0$
的线性近似方程组的解。
我们用 $x + \Delta x_{nt}$代替 $x^*$，用 $w$代替 $v^*$，并将第二个方程中的梯度项换成其在 $x$附近的线性近似，从而得到：
$A(x + \Delta x_{nt})=b, \quad \nabla f(x+\Delta x_{nt})+A^Tw\approx \nabla f(x) + \nabla^2 f(x) \Delta x_{nt} + A^Tw = 0$
利用 $Ax = b$，以上方程变成：
$A\Delta x_{nt}=0, \quad \nabla^2 f(x) \Delta x_{nt} + A^Tw = -\nabla f(x)$
这上面定义的一样。

Newton减量——停止准则

我们将等式约束问题的Newton减量定义为：
$\lambda (x) = (\Delta x_{nt}^T \nabla^2 f(x) \Delta x_{nt})^{1/2}$
这和无约束情况表示的是一样的，因此也可以进行同样的解释。
$f$在 $x$处的二阶泰勒近似为：
$\hat{f}(x+v) = f(x) + \nabla f(x)^T v + (1/2) v^T \nabla^2 f(x) v$
$f(x)$与二次模型之间的差值满足：
$f(x) - \inf \{\hat{f}(x+v) | A(x+v) = b\} = \lambda (x)^2/2$
从上面可以看出， $\lambda^2(x)/2$对 $x$处的 $f(x) - p^*$给出了基于二次模型的一个估计，这可以作为设计好的停止准则的基础。

可行下降方法的算法

注意，下面的算法初始点为可行点。

Newton方法和消除法

对原始问题采用Newton方法的迭代过程和对利用消除法简化后采用Newton方法过程完全一致，证明翻阅《凸优化》。