平面上任意椭圆与点的位置关系

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/rongdongzhu1/article/details/89917366

平面上任意椭圆与点的位置关系

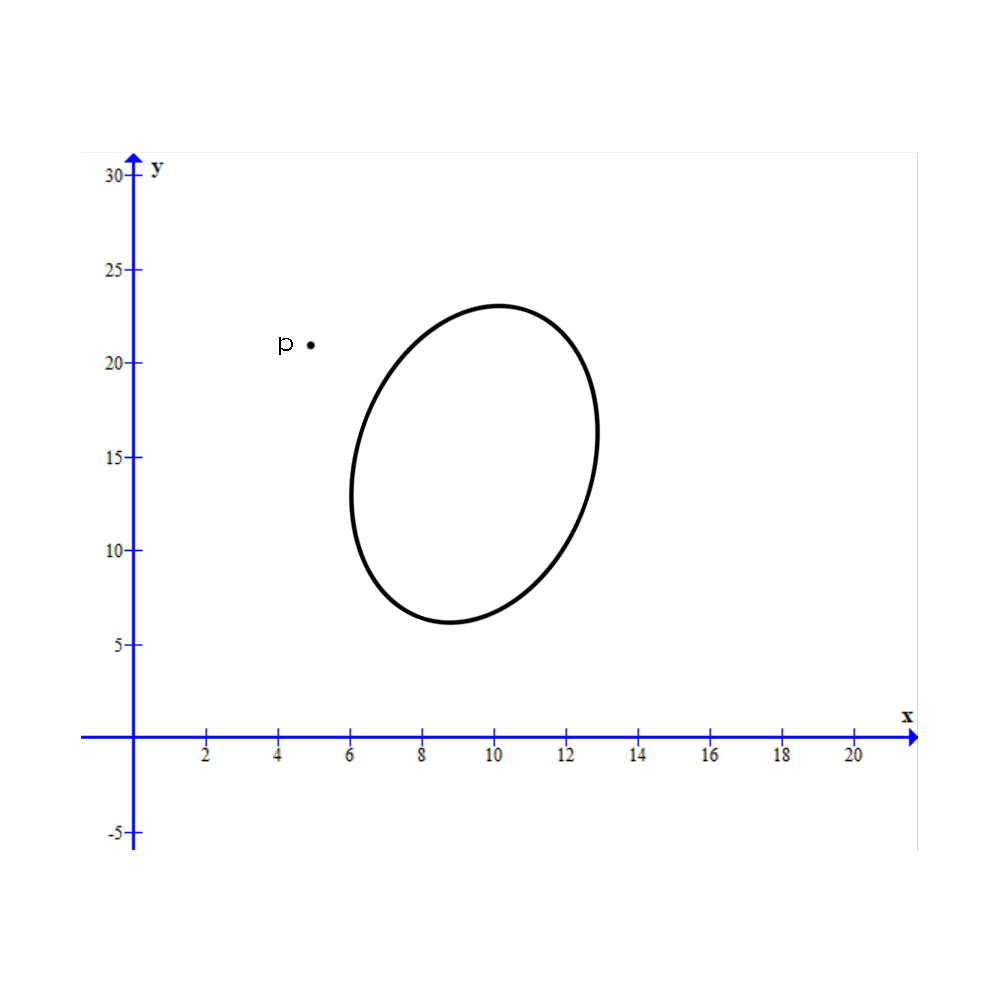
问题描述 : 如上图所示，我们的目的是判断在二维空间中任意一椭圆与任意一点 $p_i(x_i,y_i)$的位置关系，这样的位置关系有三种 : 1 点在椭圆上; 2 点在椭圆中; 3 点在椭圆外。

解决思路 :

从最简单的开始讲起, 在初中时候学到过，对于一个焦点在 $x$轴或 $y$轴的椭圆来讲有标准方程 :
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
或者
$\frac{y^2}{a^2} + \frac{x^2}{b^2} = 1$
利用标准方程，判断点与椭圆的位置关系十分容易，以焦点在 $x$轴上的椭圆为例, $\forall p(x_i,y_i)\in R^2$，这里不加证明的给出位置关系的判别式 :
(1) 若
$\frac{x_i^2}{a^2} + \frac{y_i^2}{b^2} < 1$
点在椭圆内；
(2) 若
$\frac{x_i^2}{a^2} + \frac{y_i^2}{b^2} = 1$
点在椭圆上；
(3) 若
$\frac{x_i^2}{a^2} + \frac{y_i^2}{b^2} > 1$
点在椭圆外。
这一块证明的资料很多，在此就不再赘述了。

---

现在将问题泛化 : 对于任意的一个椭圆如何求其与点 $p_i$的关系。根据上面的结论我们可以很自然的思考，如果通过一种坐标系的变换，将任意的椭圆都变为焦点在 $x$轴，或 $y$轴的椭圆，那么其与点 $p_i$位置关系的判断将是十分容易，只需要带入已知公式即可，根据这样的思路，我们建立如下坐标系。

如上图所示，在新的坐标系 $x'0'y'$中，椭圆的焦点处于坐标轴上，可以使用椭圆的标准方程进行求解，唯一的问题是如何将任给一点 $p_i$变换到 $x'0'y'$，证明的方式有很多种，在此选用基变换.
下述方法中,变换后向量的起点 $0'$的坐标是 $(x_0,y_0)$点，为了满足这个条件，首先对 $p_i$进行简单的平移变换，
$x_i = x_i - x_0 \\ y_i = y_i - y_0$
注 : $(x_0,y_0)$ 是椭圆圆心坐标.

求解 :
在原始坐标系 $x0y$中选取一组单位正交基 $\{ \vec{e_1},\vec{e_2} \},\vec{e_1} = (1,0),\vec{e_2} = (0,1)$，显然 $\vec{p_i} = x_i \vec{e_1} + y_i \vec{e_2}$.
如上图先将 $\vec{e_1},\vec{e_2}$旋转 $\theta$角，根据向量旋转公式:
$(\vec{e_1'})^T = \begin{bmatrix} \cos(\theta)& -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 0 \end{bmatrix} \\ (\vec{e_2'})^T = \begin{bmatrix} \cos(\theta)& -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 1 \end{bmatrix}$
综上 $\vec{e_1'} = \left ( \cos \theta ,\sin\theta \right ),\vec{e_2'} = (-sin\theta,cos\theta)$, 显然其满足这几点 :
(1) $\vec{e_1'},\vec{e_2'}$ 线性无关
(2) $\vec{e_1'}\cdot\vec{e_2'} = 0$
(3) $\left | \vec{e_1'} \right | = \left | \vec{e_2'} \right | = 1$
以上通过旋转矩阵求出了新坐标系下的一组正交基，下面只需要求 $\vec{p_i}$在新的基下的表示即可,解法有多种，下面展示一种通过求过度矩阵来进行求解的方法 :
将 $\vec{e_1'},\vec{e_2'}$通过 $\vec{e_2},\vec{e_2}$进行表示 :
$\vec{e_1'} = \cos\theta \cdot \vec{e_1} + \sin\theta \cdot \vec{e_2} \\ \vec{e_2'} = -\sin\theta \cdot \vec{e_1} + \cos\theta \cdot \vec{e_2} \\$
由上可以求出过渡矩阵
$C = \begin{bmatrix} \cos(\theta)& -\sin(\theta)\\ \sin(\theta) & \cos(\theta) \end{bmatrix}$
所以 $\vec{e_1},\vec{e_2}$到 $\vec{e_1'},\vec{e_2'}$的坐标变换表示为 :
$\begin{bmatrix} x_i'\\ y_i' \end{bmatrix} = C^{-1}\cdot \begin{bmatrix} x_i \\ y_i \end{bmatrix}$
整理可以得到 :
$x' = \cos\theta \cdot x + \sin\theta \cdot y \\ y' = -\sin\theta \cdot x + \cos\theta \cdot y$
上述关系式还可以通过向量间的投影关系得到.

最后将变换后的 $(x'_i,y'_i)$带入判别式，计算即可。