数据预处理
归一化
特点:通过对原始数据进行变换把数据映射到(默认为[0,1])之间
当数据中几个特征同等重要时:进行归一化,目的是让某一个特征对最终结果不会造成更大的影响
公式:x’ = (x-min)/(max-min) 注:作用于每一列,max为一列的最大值,min为一列的最小值,那么x’为最终结果
sklearn归一化API:
sklearn.preprocessing.MinMaxScaler
MinMaxScaler语法
- MinMaxScalar(feature_range=(0,1)…)
- 每个特征缩放到给定范围(默认[0,1])
- MinMaxScalar.fit_transform(X)
- X: numpy array格式的数据 [n_samples,n_features]
- 返回值:转换后的形状相同的 array
归一化步骤:
- 1、实例化MinMaxScalar
- 2、通过fit_transform转换
# 最大最小值归一化处理
from sklearn.preprocessing import MinMaxScaler
data = [
[90, 2, 10, 40],
[75, 3, 13, 46],
[60, 4, 15, 45]
]
mm = MinMaxScaler()
_data = mm.fit_transform(data)
print("归一化后的结果:\n", _data)
print(type(_data))
归一化后的结果:
[[1. 0. 0. 0. ]
[0.5 0.5 0.6 1. ]
[0. 1. 1. 0.83333333]]
<class 'numpy.ndarray'>
归一化总结:
注意在特定场景下最大值最小值是变化的,另外,最大值与最小值非常容易受异常点影响,所以这种方法鲁棒性较差,只适合传统精确小数据场景。
标准化处理
- 特点:通过对原始数据进行变换把数据变换到均值为0,标准差为1范围内
- 公式:
- x’= (x-mean)/σ
- σ= √std,
- std为方差,std= ((x1-mean)2+(x2-mean)2+⋯)/(n(每个特征的样本数)),
注:作用于每一列,mean为平均值,σ为标准差(考量数据的稳定性)
sklearn特征化API:
scikit-learn.preprocessing.StandardScaler
StandardScaler语法
- StandardScaler(…)
- 处理之后每列来说所有数据都聚集在均值0附近标准差为1
- StandardScaler.fit_transform(X)
- X: numpy array格式的数据 [n_samples,n_features]
- 返回值:转换后的形状相同的array
- StandardScaler.mean_
- 原始数据中每列特征的平均值
- StandardScaler.std_
- 原始数据每列特征的方差
标准化步骤
- 1、实例化StandardScaler
- 2、通过fit_transform转换
# 标准化
from sklearn.preprocessing import StandardScaler
data = [
[1, -1, 3],
[2, 4, 2],
[4, 6, -1]
]
sd = StandardScaler()
_data = sd.fit_transform(data)
print("标准化后的结果:\n", _data)
print("均值:\n", sd.mean_)
print("标准差:\n", sd.scale_)
标准化后的结果:
[[-1.06904497 -1.35873244 0.98058068]
[-0.26726124 0.33968311 0.39223227]
[ 1.33630621 1.01904933 -1.37281295]]
均值:
[2.33333333 3. 1.33333333]
标准差:
[1.24721913 2.94392029 1.69967317]
标准化总结
在已有样本足够多的情况下比较稳定,适合现代嘈杂大数据场景。
对于归一化来说:如果出现异常点,影响了最大值和最小值,那么结果显然会发生改变
对于标准化来说:如果出现异常点,由于具有一定数据量,少量的异常点对于平均值的影响并不大,从而方差改变较小。
数据降维
这里的降维并不是数组里面的维度,而是特征的数量
特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征,特征在选择前和选择后可以改变值、也不改变值,但是选择后的特征维数肯定比选择前小,毕竟我们只选择了其中的一部分特征。
特征选择:删除低方差的特征
- 特征选择原因:
- 冗余:部分特征的相关度高,容易消耗计算性能
- 噪声:部分特征对预测结果有负影响
VarianceThreshold语法
-
VarianceThreshold(threshold = 0.0)
- 删除所有低方差特征
-
Variance.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征。
流程:
1、初始化VarianceThreshold,指定阀值方差
2、调用fit_transform
# 特征选择:删除低方差的特征
from sklearn.feature_selection import VarianceThreshold
data = [
[0, 2, 0, 3],
[0, 1, 4, 3],
[0, 1, 1, 3]
]
# 删除方差低于阈值 threshold 的特征数据
var = VarianceThreshold(threshold=1.0) # 默认是删除 threshold=0 的特征,即删除重复数据
_data = var.fit_transform(data)
print("特征选择后的数据:\n", _data)
特征选择后的数据:
[[0]
[4]
[1]]
PCA降维
主成分分析:当特征的数量达到上百的时候,考虑数据的简化
sklearn.decomposition
- 本质:PCA是一种分析、简化数据集的技术
- 目的:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
- 作用:可以削减回归分析或者聚类分析中特征的数量
高维度数据容易出现的问题:特征之间通常是线性相关的
PCA语法
- PCA(n_components=None)
将数据分解为较低维数空间- n_components:
- 小数0~1 表示降维后保留的信息 一般90%–95%
- 整数 减少到的特征数目
- 参数设置为"mle", 此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维
- n_components:
- PCA.fit_transform(X)
- X:numpy array格式的数据[n_samples,n_features]
- 返回值:转换后指定维度的array
# 主成分分析PCA
from sklearn.decomposition import PCA
data = [
[2, 8, 4, 5],
[6, 3, 0, 8],
[5, 4, 9, 1],
[4, 2, 3, 8]
]
# 参数设置为"mle", 此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维
# 但是要求样本数大于等于维数 n_samples >= n_features
pca = PCA(n_components='mle') # 如果是0-1的数值,则表示保留 xx% 的信息,如果是整数,则是减少到的特征数目
_data = pca.fit_transform(data)
print("PCA降维后的数据:\n", _data)
print("每个特征维度的方差比例:\n", pca.explained_variance_ratio_)
print("每个特征维度的方差:\n", pca.explained_variance_)
print("保留的特征数:\n", pca.n_components_)
PCA降维后的数据:
[[ 1.28294902 4.20966885 0.08792057]
[-4.93026101 -0.81441098 -1.37994968]
[ 6.44671526 -2.04634465 -0.35684154]
[-2.79940327 -1.34891322 1.64887066]]
每个特征维度的方差比例:
[0.72105482 0.23341311 0.04553207]
每个特征维度的方差:
[25.11674273 8.13055677 1.58603383]
保留的特征数:
3
简单的小demo
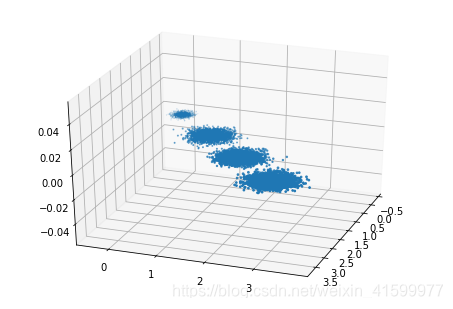
# 画出四个簇的数据样本
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets.samples_generator import make_blobs
# X为样本特征,y为样本簇类别,共1000个样本,每个样本3个特征,共4个簇
X, y = make_blobs(n_samples=10000,
n_features=3,
centers=[[3,3,3], [0,0,0], [1,1,1], [2,2,2]], # 每个簇的中心
cluster_std=[0.2, 0.1, 0.2, 0.2], # 每个簇的方差
random_state=9)
fig = plt.figure()
ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)
plt.scatter(X[:, 0], X[:, 1], X[:, 2], marker='o')
plt.show()
# 暂时不降维,还是保留3个维度,观察每个维度的方差信息
from sklearn.decomposition import PCA
pca = PCA(n_components=3)
_data = pca.fit_transform(X)
print("每个特征维度的方差比例:\n", pca.explained_variance_ratio_)
print("每个特征维度的方差:\n", pca.explained_variance_)
print("保留的特征数:\n", pca.n_components_)
每个特征维度的方差比例:
[0.98318212 0.00850037 0.00831751]
每个特征维度的方差:
[3.78521638 0.03272613 0.03202212]
保留的特征数:
3
# 保留2个维度,观察方差信息
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
_data = pca.fit_transform(X)
print("每个特征维度的方差比例:\n", pca.explained_variance_ratio_)
print("每个特征维度的方差:\n", pca.explained_variance_)
print("保留的特征数:\n", pca.n_components_)
每个特征维度的方差比例:
[0.98318212 0.00850037]
每个特征维度的方差:
[3.78521638 0.03272613]
保留的特征数:
2
# 画出两个维度的数据分布图
from matplotlib import pyplot as plt
fig = plt.figure()
plt.scatter(_data[:, 0], _data[:, 1], marker="o")
plt.show()

由上图可见,降维后的数据依然可以很清楚的看到我们之前三维图中的4个簇
# 保留 99% 的信息
from sklearn.decomposition import PCA
pca = PCA(n_components=0.99)
_data = pca.fit_transform(X)
print("每个特征维度的方差比例:\n", pca.explained_variance_ratio_)
print("每个特征维度的方差:\n", pca.explained_variance_)
print("保留的特征数:\n", pca.n_components_)
print("第一个主成分占了98.3%的方差比例,第二个主成分占了0.8%的方差比例,两者一起可以满足我们的阈值。")
print("-"*100)
# 保留 95% 的信息
pca = PCA(n_components=0.95)
_data = pca.fit_transform(X)
print("每个特征维度的方差比例:\n", pca.explained_variance_ratio_)
print("每个特征维度的方差:\n", pca.explained_variance_)
print("保留的特征数:\n", pca.n_components_)
print("可见只有第一个投影特征被保留。这也很好理解,第一个主成分占投影特征的方差比例高达98%。只选择这一个特征维度便可以满足95%的阈值")
每个特征维度的方差比例:
[0.98318212 0.00850037]
每个特征维度的方差:
[3.78521638 0.03272613]
保留的特征数:
2
第一个主成分占了98.3%的方差比例,第二个主成分占了0.8%的方差比例,两者一起可以满足我们的阈值。
----------------------------------------------------------------------------------------------------
每个特征维度的方差比例:
[0.98318212]
每个特征维度的方差:
[3.78521638]
保留的特征数:
1
可见只有第一个投影特征被保留。这也很好理解,第一个主成分占投影特征的方差比例高达98%。只选择这一个特征维度便可以满足95%的阈值