深度学习--2.线性回归

版权声明：原创作品，欢迎转载 https://blog.csdn.net/xf8964/article/details/89607743

我们知道神经网络可以用于分类，可以以用于线性回归，将数据拟合成一条合适的线或一个合适的面，下面我们所说线性回归中的问题

绝对值技巧

现在假设我们有一个点（p，q）和一条直线 $y = w_1x +b$，其中 $w_1$是斜率，b是y轴截距，并且点在直线的上方，我们现在想让直线更靠近点，直线该怎么做呢？

我们可以引入学习速率 $\alpha$，使直线变化的幅度不是很大

• 向上平移：增加b一个单位
• 旋转：让斜率加上p

$y = （w_1+ \alpha p）x +(b +\alpha)$

如果点在直线的下方

• 向下平移：减小b一个单位
• 旋转：让斜率减去p

$ $y = （w_1- \alpha p）x +(b -\alpha)$
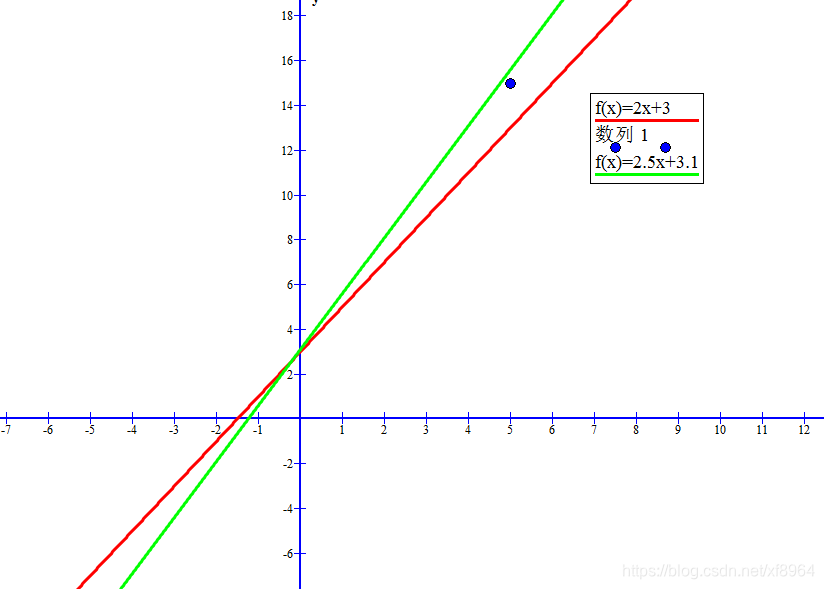
现在我们使用图形来展示这一效果，我们有一条直线 y = 2x+3 （红色的线）和点（5， 15）
点在线的上方，经过计算得到直线y = 2.5x+3.1（绿色的线）
如下图

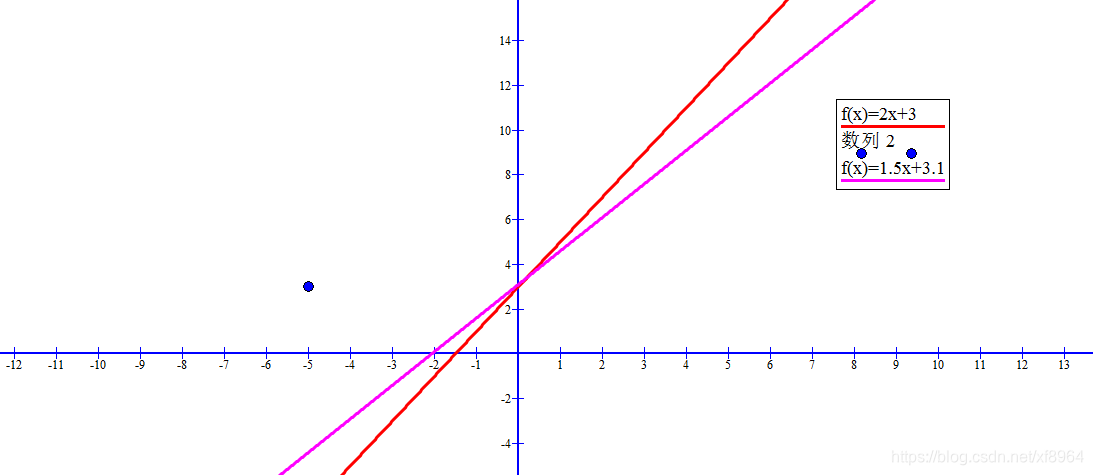
假设点坐标为（-5， 15），得到的直线为y = 1.5x+ 3.1（紫色线）如图

平方技巧

特点：距离直线进就小幅度移动，距离远的话就大幅度移动，绝对值技巧不具有该特点，因为我们是使用的点到y轴的距离，跟点到直线的距离无关

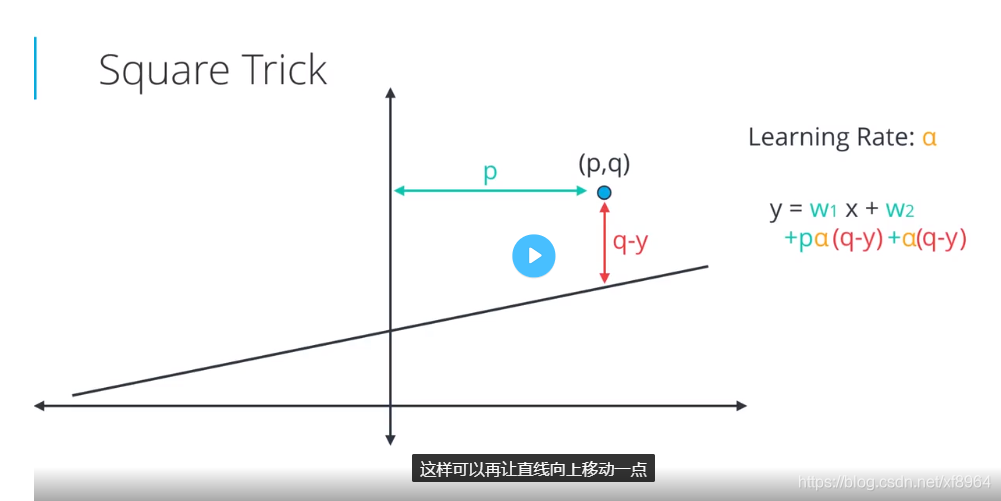
现在假设我们有一个点（p，q）和一条直线 $y = w_1x +b$，其中 $w_1$是斜率，b是y轴截距，并且点在直线的上方，我们现在想让直线更靠近点，直线该怎么做呢？

我们可以引入学习速率 $\alpha$，使直线变化的幅度不是很大

• 向上平移：增加b，加上 $\alpha (q - y)$
• 旋转：让斜率加上 $\alpha$p(q-y)

$y = （w_1+ \alpha p(q-y)）x +(b +\alpha(q-y))$

如果点在直线的下方的时候(q-y)是个负数，那么上面的方程也适用，所以两种情况一个方程都适用

平方误差函数的梯度下降法推导

平均绝对值误差

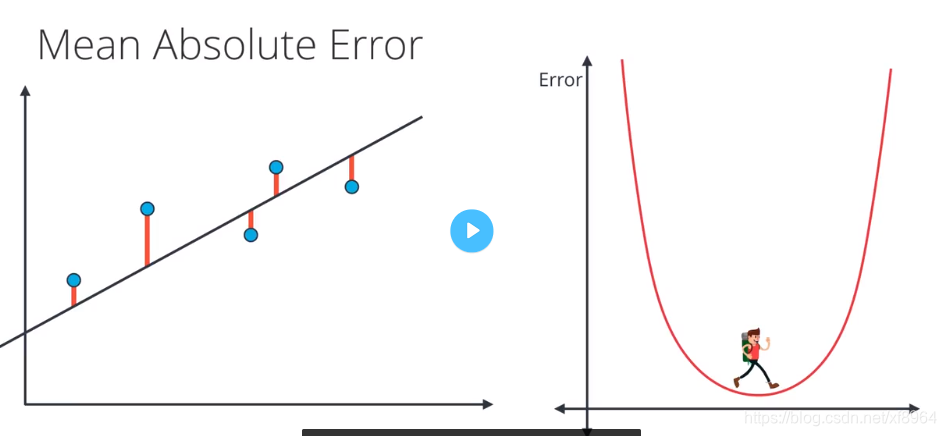
我们要判定一个模型的好坏，那就得看其误差函数的值的大小，在线性回归中有两种误差公式，一种是平均绝对值误差，一种是平均平方误差，我们先用模型预测点的值，延后用点的真实值减去预测值然后取绝对值，得到其误差值，这里的误差物理含义是在最值方向上点到直线的距离（不是点到直线的垂直距离）

公式为：
$Error = \frac{1}{m} \sum_{i=1}^{m}|y -\hat{y}|$
我们加绝对值的原因是不能让负的误差抵消掉正的误差
初始的时候误差如下图所示

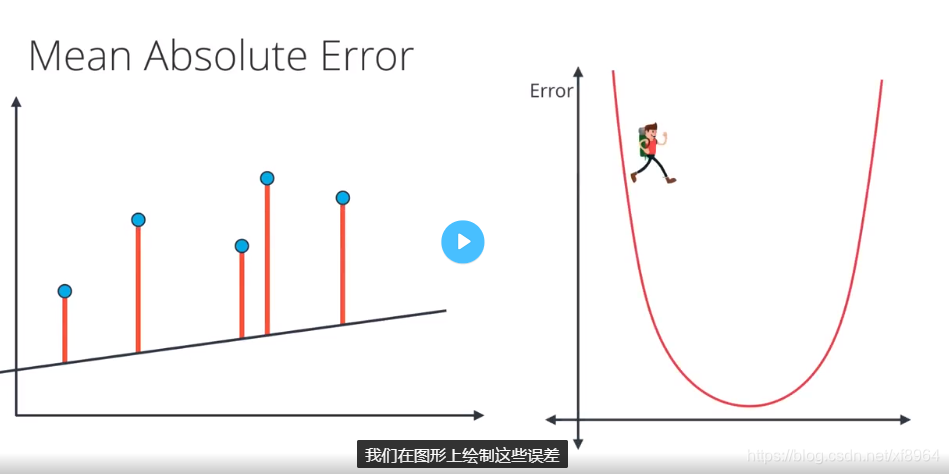
然后我们经过梯度下降法找到最小的误差

平均平方误差 均方误差

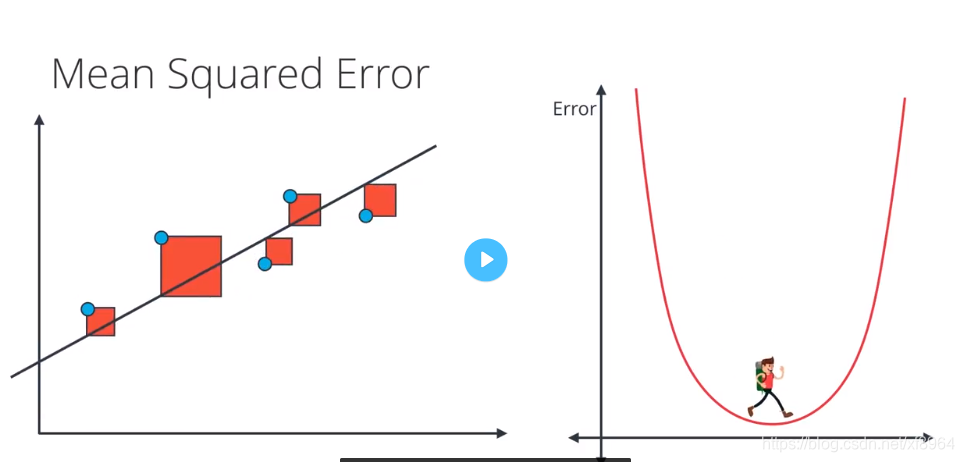
这里我们讲解什么是平均平方误差函数，我们在上面讲到了平均绝对值误差，其实就是对误差求绝对值处理，这里的平均平方误差就是对误差做平方处理

公式：
$Error = \frac{1}{2m} \sum_{i=1}^{m}(y -\hat{y})^2$

公式中分母上的2是为了对误差函数求导数方便，因为常数对收敛是没有影响的m是对所有误差求和之后去平均

初始状态的误差的图形为下图所示

在使用梯度下降法后得到最小的误差

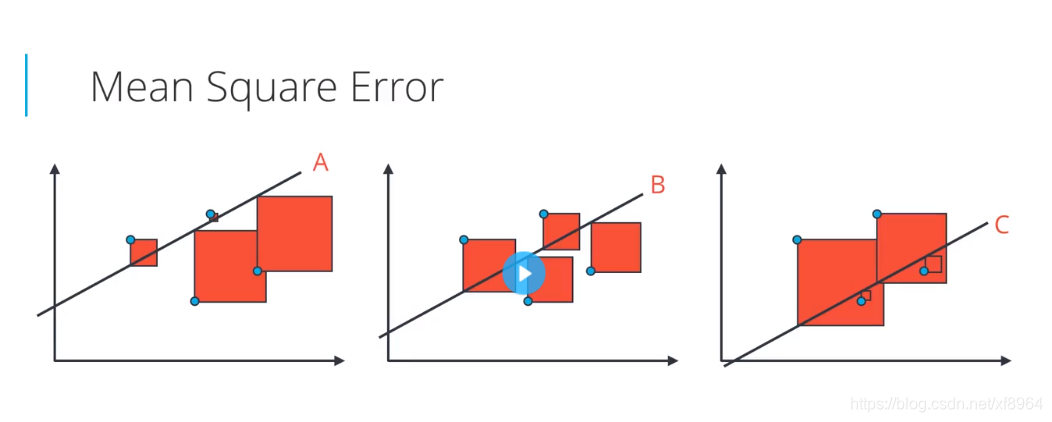
平均绝对值误差 VS 平均平方误差

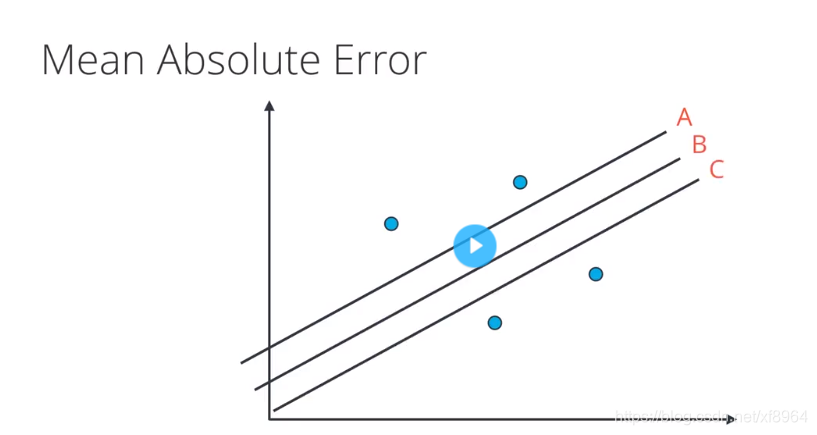
对于上图中的数据点，三条拟合的直线中，那条最合适呢？应该是B直线更合适一些，我们该用上面那个方法来找到这条直线呢？如果用绝对值误差，那么这三条线的误差是相同的，如果用平方误差，那中间的线误差最小

线性回归注意事项

最适用于线性数据

线性回归会根据训练数据生成直线模型。如果训练数据包含非线性关系，你需要选择：调整数据（进行数据转换）、增加特征数量（参考下节内容）或改用其他模型。

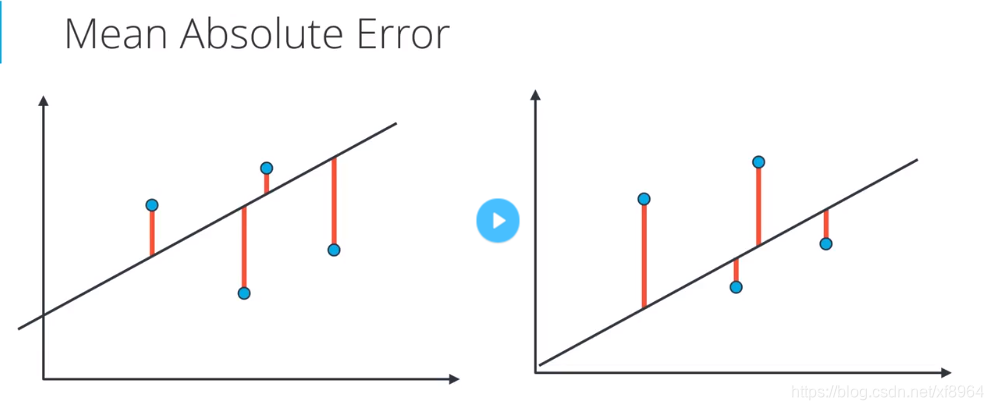
容易受到异常值影响

线性回归的目标是求取对训练数据而言的 “最优拟合” 直线。如果数据集中存在不符合总体规律的异常值，最终结果将会存在不小偏差。

在第一个图表中，模型与数据相当拟合。

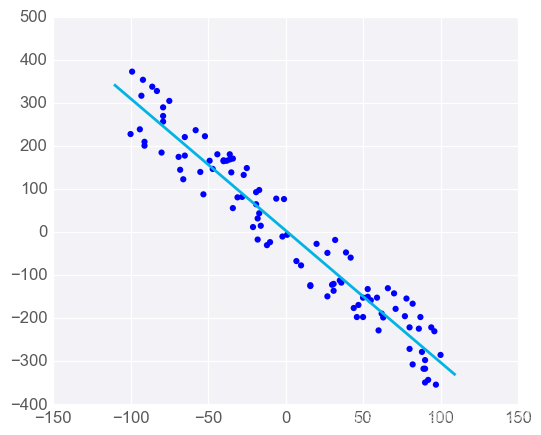
但若添加若干不符合规律的异常值，会明显改变模型的预测结果

在大多数情况下，模型需要基本上能与大部分数据拟合，所以要小心异常值！

正则化

正则化可以改善我们的模型，确保不会过度拟合的有效技巧，这个技巧可以用于回归和分类

现在如上图，有一些数据，左边是用线性回归方程拟合数据，右边是用高斯多项式来拟合数据，我们可以看到左边的模型有两个点分类错误，但是通用性强，右边的模型没有分类错误的点，但是有点过拟合，通用不强

首先我们通过分类误差类比较一下两个模型的好坏，左边的模型有两个分类错误，右边没有分类错误，如黄色误差，长度表示误差大小，可以看到右边的模型要好，

我们再来将权重作为误差的一部分，左边的模型只有两个权重，右边的模型有6个权重，如绿色的误差，那么左边的模型的误差要比右边模型的误差要小很多，我们可以认为左边的模型要好很多，并且左边的模型简单，

我们接下来讲解怎么将绿色的部分转化为误差的一部分

L1正则化

对于上面的多项式模型我们的L1正则如下，就是将的系数的绝对值相加
对于直线模型的L1正则如下

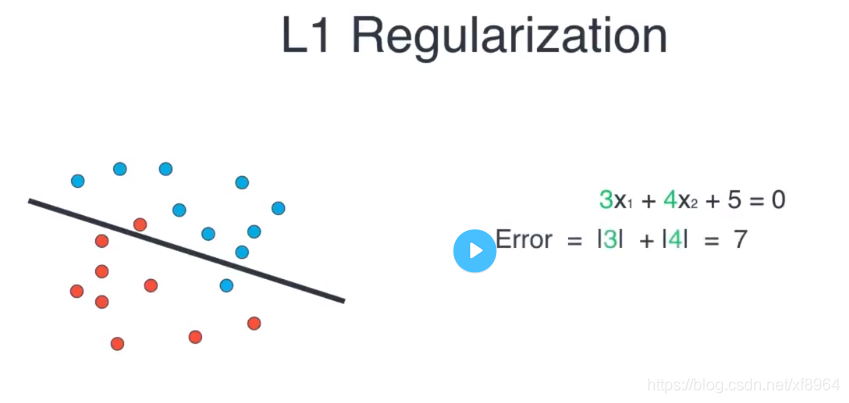
L1正则我们可以理解为系数的绝对值相加

L2正则化

对于多项式的L2正则化
对于直线的L2正则如下

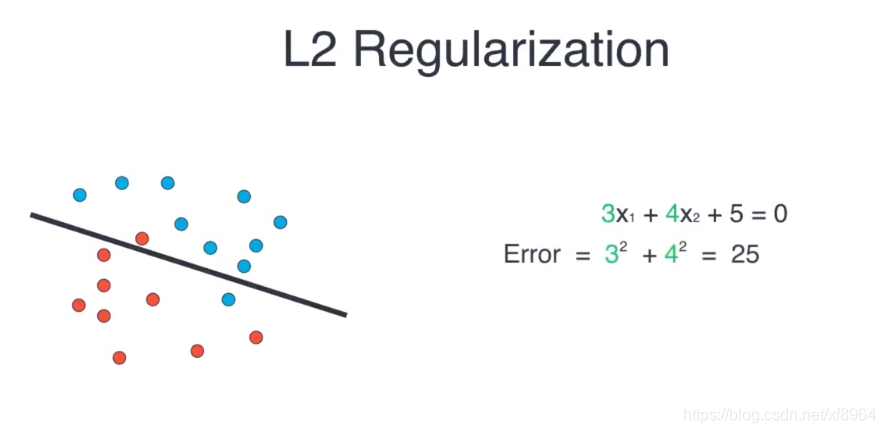
L2正则我们可以理解为系数的平方和

那我们的问题是怎么对误差进行调优，因为我们想要使用复杂模型，于是我们引入参数 $\lambda$, $\lambda$的作用是可以乘以复杂误差，可以是绿色部分的误差变大或变小，当我们使用很小的 $\lambda$时，绿色部分的参数就变得很小，所以复杂的模型胜出

当我们使用大的 $\lambda$时，绿色的误差部分就会变得很大

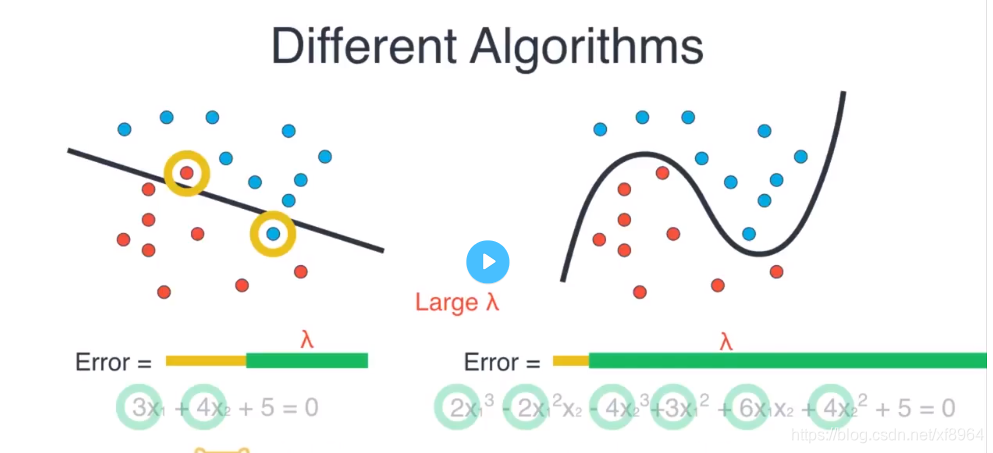
所以当 $\lambda$很大的时候就用简单模型， $\lambda$很小的时候就用复杂模型

L1 VS L2 正则化