【数学基础】最小二乘法

版权声明：【fishing-pan：https://blog.csdn.net/u013921430转载请注明出处】 https://blog.csdn.net/u013921430/article/details/84344510

【fishing-pan：https://blog.csdn.net/u013921430 转载请注明出处】

前言

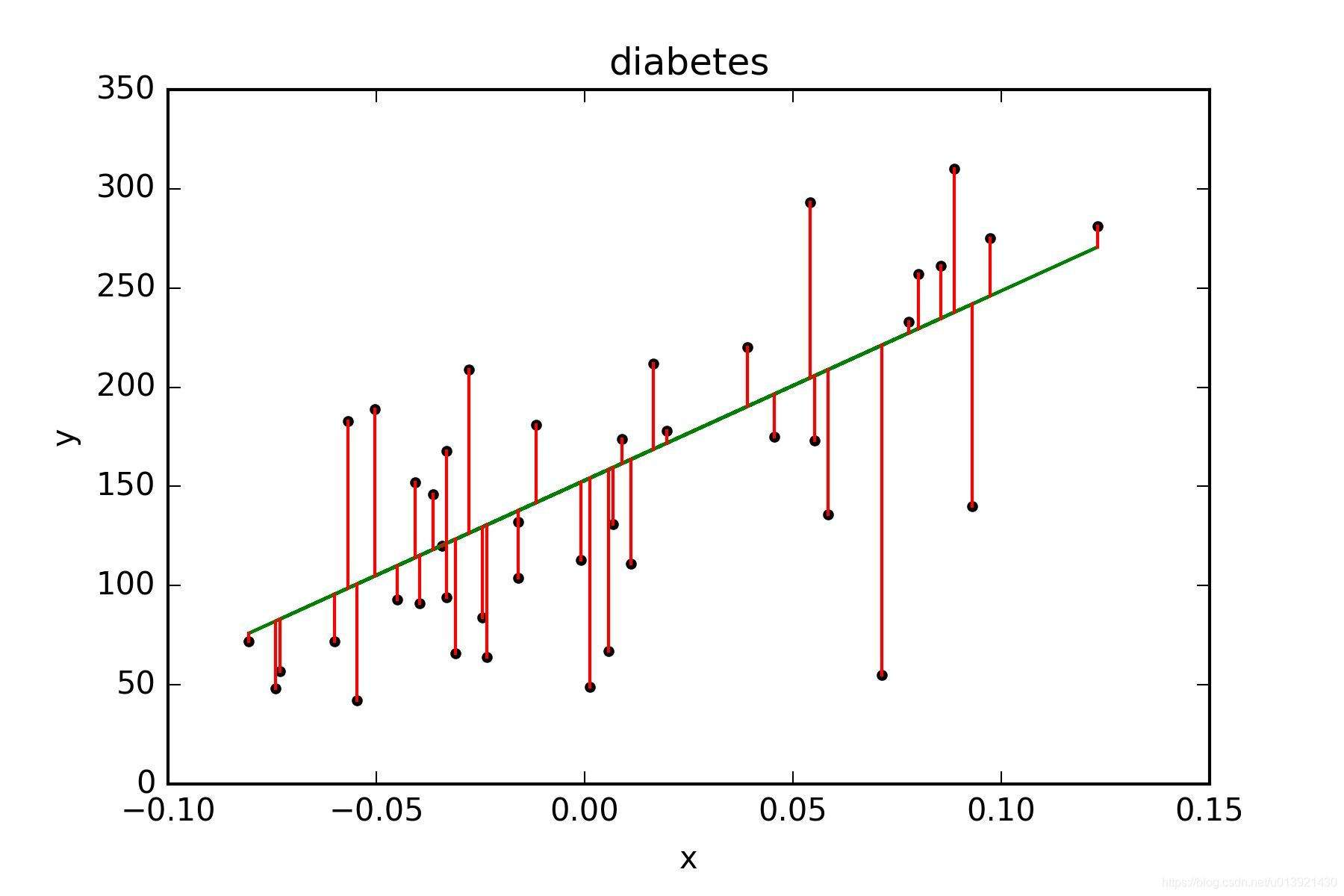
   当我们有 $N$组数据，希望能够用一个函数来拟合这组数据的分布情况时，首先想到的就是最小二乘法。最小二乘法是线性回归中最基础也是最常用模型，它也可以用来拟合高次多项式。

什么是最小二乘法

  那么，什么是最小二乘法呢？将我们手中已有的数据表示成一个集合，（为了简化模型，暂且只考虑输入属性只有 $x$一个的情况） $D=\left \{ (x_{1};y_{1}),(x_{2};y_{2}),\cdots ,(x_{n};y_{n}) \right \}$
  首先假设最终得到的线性模型为；
$y=ax+b$

  如上图所示，绿色的线条为所求的回归模型，黑色点为实际样本输入数据，红色线段为实际值与模型预测值之间的欧氏距离，用以下公式表示；
$e_{i}=\left \| ax_{i}+b-y_{i} \right \|$
  为了让最终所求的模型尽量准确地表现数据分布规律，我们需要让 $e_{i}$的和尽可能的小，所以 $(a^{*},b^{*})$在 $e_{i}$的和取最小值时取得；
$(a^{*},b^{*})=\underset{(a,b)}{argmin}\sum_{i=1}^{n}\left \| ax_{i}+b-y_{i} \right \|$
   但是上述式子中的绝对值是不可导的，求解困难。因此采用均方误差来代替绝对值。
$(a^{*},b^{*})=\underset{(a,b)}{argmin}\sum_{i=1}^{n} (ax_{i}+b-y_{i} )^{2}$
  这种基于均方误差来进行模型求解的方法就叫最小二乘法，也叫最小平方法。

参数推导

  首先还是来看上面提到的最简单的情况。令；
$E(a,b)=\sum_{i=1}^{n} (ax_{i}+b-y_{i} )^{2}$
   $E$是关于 $a$与 $b$的二次函数，只会有一个极值点。而很明显，让 $E$取极大值的 $(a,b)$出现在空间中无限远处的，是不存在的。所以当 $(a,b)$让 $E$取得极值时， $E$取得极小值，分别对 $a$、 $b$求偏导。
$\begin{aligned} \frac{\partial E}{\partial a}&=2\sum_{i=1}^{n} (ax_{i}+b-y_{i} )x_{i}\\ &=2(\sum_{i=1}^{n} ax_{i}^{2}+\sum_{i=1}^{n}bx_{i}-\sum_{i=1}^{n}y_{i}x_{i})\\&=2(\sum_{i=1}^{n} ax_{i}^{2}+b*n\bar{x}-\sum_{i=1}^{n}y_{i}x_{i}) \end{aligned}$
$\frac{\partial E}{\partial b}=2\sum_{i=1}^{n} (ax_{i}+b-y_{i} )=2(a*n\bar{x}+nb-n\bar{y})$
  令；
$\frac{\partial E}{\partial a}=0，\frac{\partial E}{\partial b}=0$
  可得；
$a=\frac{\sum_{i=1}^{n}x_{i}y_{i}-n\bar{x}\bar{y}}{\sum_{i=1}^{n}x_{i}^{2}-n\bar{x}^{2}}$
$b=\bar{y}-a\bar{x}=\frac{\bar{y}\sum_{i=1}^{n}x_{i}^{2}-\bar{x}\sum_{i=1}^{n}x_{i}y_{i}}{\sum_{i=1}^{n}x_{i}^{2}-n\bar{x}^{2}}$
  由于，
$\begin{aligned} \sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})&=\sum_{i=1}^{n}(x_{i}y_{i}-x_{i}\bar{y}-y_{i}\bar{x}+\bar{x}\bar{y})\\ &=\sum_{i=1}^{n}x_{i}y_{i}-\bar{y}\sum_{i=1}^{n}x_{i}-\bar{x}\sum_{i=1}^{n}y_{i}+n\bar{x}\bar{y}\\ &=\sum_{i=1}^{n}x_{i}y_{i}-n\bar{x}\bar{y} \end{aligned}$
  同理，
$\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}=\sum_{i=1}^{n}x_{i}^{2}-n\bar{x}^{2}$
  所以 $a$还可以表示成，
$a=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}$

多元线性回归

  上述的推导中输入属性数目为一，在一般的情况下，样本的属性会有多个，所以通过矩阵的形式将上述推导过程进行推广。假设数据集 $D$中样本属性有 $d$个；将第 $i$个样本可以表示成以下形式；
$(x_{i}^{1};x_{i}^{2};\cdots ;x_{i}^{d};y)$
  用向量 ${\textbf{x}}_{i}$表示 $d$ 个属性， ${\textbf{w}}$表示参数的向量;
${\textbf{x}}_{i}=(x_{i}^{1};x_{i}^{2};\cdots ;x_{i}^{d})$
${\textbf{w}}=(w_{1};w_{2};\cdots ;w_{d})$
  则回归模型可以表示成；
$f({\textbf{x}}_{i})={\textbf{w}}^{T}{\textbf{x}}_{i}+b$
  为了便于讨论，令
$\hat{\textbf{w}}=({\textbf{w}};b)$
  对应的将 ${\textbf{x}}$也增加一项；
${\textbf{x}}_{i}=(x_{i}^{1};x_{i}^{2};\cdots ;x_{i}^{d};1)$
$f({\textbf{x}}_{i})=\hat{\textbf{w}}^{T}{\textbf{x}}_{i}$
${\textbf{X}}=\begin{pmatrix} x_{1}^{1} & x_{1}^{2} & \cdots & x_{1}^{d} &1 \\ x_{2}^{1} & x_{2}^{2} & \cdots & x_{2}^{d} &1\\ \vdots & \ddots & \ddots &\vdots & \vdots \\ x_{n}^{1} & x_{n}^{2} & \cdots & x_{n}^{d} &1 \end{pmatrix}=\begin{pmatrix} {\textbf{x}}_{1}^{T} &1 \\ {\textbf{x}}_{2}^{T} &1 \\ \vdots &\vdots \\ {\textbf{x}}_{n}^{T} & 1 \end{pmatrix}$
  同样地； ${\textbf{y}}=({y}_{1};{y}_{2};\cdots;{y}_{n})$，那么与上面的类似，有;
$\hat{\textbf{w}}^{*}=\underset{\hat{\textbf{w}}}{arg\, min}({\textbf{y}}-{\textbf{X}}\hat{\textbf{w}})^{T}({\textbf{y}}-{\textbf{X}}\hat{\textbf{w}})$
  令 $E=({\textbf{y}}-{\textbf{X}}\hat{\textbf{w}})^{T}({\textbf{y}}-{\textbf{X}}\hat{\textbf{w}})$；对 $\hat{\textbf{w}}$求偏导数；
$\frac{\partial E}{\partial \hat{\textbf{w}}}=2{\textbf{X}}^{T}({\textbf{X}}\hat{\textbf{w}}-\textbf{y})$
  最终所求
$\hat{\textbf{w}}^{*}=({\textbf{X}}^{T}{\textbf{X}})^{-1}{\textbf{X}}^{T}\textbf{y}$

继续推广延伸

  更一般的，可以将这种线性回归用于非线性函数的拟合；例如对于对数函数；
$f({\textbf{x}}_{i})=y=ln({\textbf{w}}^{T}{\textbf{x}}_{i}+b)$
  可以利用反函数，将其转换成 $h=e^{y}={\textbf{w}}^{T}{\textbf{x}}_{i}+b$；成为一个线性回归的问题，最终再转换成对数形式；

  甚至可以用最小二乘法拟合多项式曲线。
$y=a_{0}+a_{1}x+a_{2}x^{2}+\cdots +a_{m}x^{m}$
${\textbf{X}}=\begin{pmatrix} x_{1}^{m} & x_{1}^{m-1} & \cdots & x_{1}^{1} &1 \\ x_{2}^{m} & x_{2}^{m-1} & \cdots & x_{2}^{1} &1\\ \vdots & \ddots & \ddots &\vdots & \vdots \\ x_{n}^{m} & x_{n}^{m-1} & \cdots & x_{n}^{1} &1 \end{pmatrix}$
  此时上标 $m$不再表示第 $m$个属性，而是表示 $m$次幂；在修改过 ${\textbf{X}}$后，最终 $\hat{\textbf{w}}^{*}$依然表示为；
$\hat{\textbf{w}}^{*}=({\textbf{X}}^{T}{\textbf{X}})^{-1}{\textbf{X}}^{T}\textbf{y}$

Matlab 实现高次多项式拟合

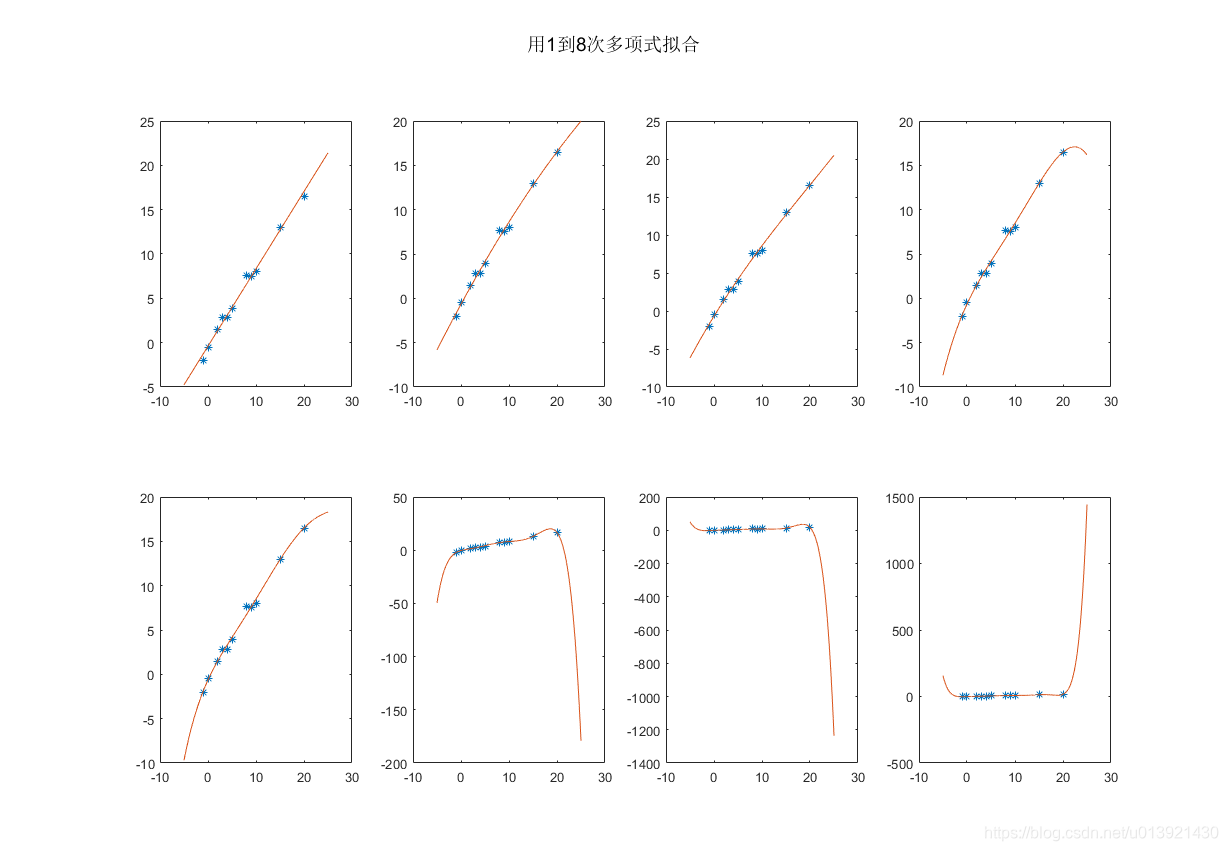
  用Matlab实现了最小二乘法一元高次多项式拟合；代码如下；

**%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%不用先生，2018.11.22，最小二乘法一元高次多项式拟合
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
clear all;
xi=[-1,0,2,3,4,5,8,9,10,15,20];
yi=[-2,-0.5,1.5,2.8,2.8,3.9,7.6,7.5,8,13,16.5];

[~,n]=size(xi);
m=8;     %%最高8次多项式；
W=zeros(m+1,m);

for i=1:m
     X=zeros(n,i+1);    %%创建一个n*+1的矩阵；
    for j=1:n
        for s=1:i          
            X(j,s)=xi(j)^(i+1-s);   %%计算矩阵中每一个元素的值
        end
        X(j,i+1)=1;
    end
    XX=inv(X'*X)*X'*yi';  %%得到系数并赋值
    for j=1:i+1
        W(j,i)=XX(j);
    end 
end
   
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%构造方程，画图
x=-5:0.01:25;
for i=1:m
    y=W(1,i)*x.^i;
    for j=2:i+1
        y=y+W(j,i)*x.^(i-j+1);
    end   
    subplot(2,4,i);
    plot(xi,yi,'*');
    hold on;
    plot(x,y);
    hold off
end
suptitle('用1到8次多项式拟合')
**

  很明显，在高次多项式拟合时，曲线边缘出现了龙格现象。

参考

《机器学习》，周志华 著，清华大学出版社；

已完。。