目录:
(随机变量,概率分布)
(联合概率,边缘概率,独立性,条件概率以及在贝叶斯上的应用)
(期望,方差,标准差,大数定理)
(概率密度函数,概率分布函数以及随机变量的变换,联合概率分布函数,高斯分布以及中心极限定理)
(协方差和相关系数,协方差矩阵和变量变换,标准多元正态分布到一般多元正态分布
引出协方差矩阵的对角化,对对角化的协方差矩阵绘制(椭圆)等高线图!)

(以上是本书的重点,对基础知识的不同看法!)
(以下书中只是提到,需要自己好好钻研!)
第一章:概率的定义
1.随机变量
定义:类似于函数的一个形式,传入参数会返回一个映射值,总的来看随机变量就是一个函数!


2.概率分布
定义:概率分布是定义在随机变量之上的形式,是随机变量的值域与定义域的对应关系,是对随机变量函数的一种描述!


:只要得到随机变量X,就可以得到它的概率分布!
第二章:多个随机变量之间的关系
1.联合概率与边缘概率的预热
边缘概率:边缘概率与所有面积(1)的关系
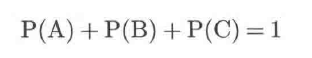
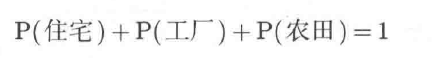
联合概率:联合概率与边缘概率的关系(就是两个随机变量之间的交集)


最终:全面积和联合概率的关系

2.条件概率的预热
条件概率:就是两个随机变量的交集占某一个随机变量的面积多少!比如:住宅和A的交集占A的百分比!!
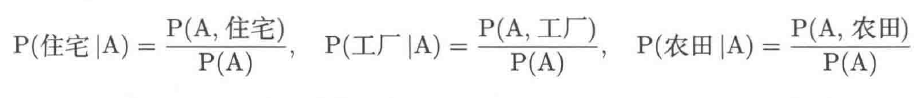
取加权后的交集仍然可以归一化!
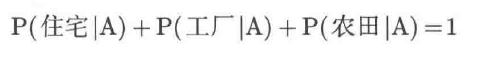
3.贝叶斯公式的预热


4.独立性的预热
从联合概率和条件概率来说明,独立性就是两者的发生没有关系!


预热就此完毕!
5.联合概率与边缘概率
定义:(注意假设了两个随机变量)

联合概率和边缘概率的关系:

联合概率和边缘概率的在一个解释:

6.条件概率
定义:(在条件X=a的分布下,Y的分布是如何的!)

例子:




练习题:

7.联合概率,条件概率,边缘概率总结

8.三个或者更多的随机变量



9.贝叶斯公式(应用条件概率来解决逆问题)
逆问题定义:就是指那些需要从结果去反推原因的问题,通常是因为原因X很难被观测到,我们就通常会通过其原因X(只是限定了Y的分布)来反推出结果Y!
问题设置:


贝叶斯总结:其实就是把概率全部转化为条件概率,并且是和最终问题目标的条件概率互为逆问题,来解决很难直推的问题!而且逆问题就是:是根据X->Y再加上X的先验概率分布,由Y逆推出X的值的一个过程!
10.独立性
独立的定义:
如果随机变量X与Y独立,那么就不需要分析他们之间的关系了,可以省去很多事情,来简化操作!
如果随机变量X与Y独立,那么联合概率等于边缘概率的乘积!

练习题:
对某个事件来说明:


对某个随机变量来说明:

11.三个或更多随机变量的独立性(注意:往两个随机变量独立上去引申!)


第三章:离散值的概率分布
1.二项分布
定义:

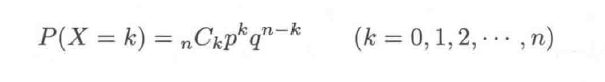
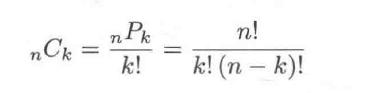
2.期望值(概率的加权取和)
定义:
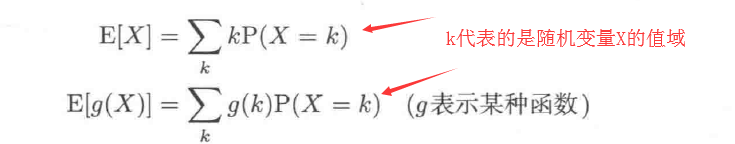


性质:



对公式的理解请看如下证明!!!


练习题:


3.方差与标准差
方差:样本值与期望值的离散程度。(值越大随机变量的值就越分散,值越小就越集中)

方差计算,还是转化为了期望值的计算!
标准差:方差的平方根。
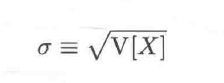
方差与标准差的性质:

练习题:



随机变量独立时,方差与均值的关系:


再来介绍一条公式:




4.大数定律
独立同分布:

平均值的期望值和平均值的方差:


大数定理:

大数定理其实就是通过对独立同分布的随机变量取平均,当n趋近于无穷的时候方差趋近于零,那么结果的值和期望值就可以基本近似的等同起来!(有没有一点bagging的思想呢!!!!当树的数量多到一定程度模型的方差趋近于零,处理了模型的过拟合问题!)
大数定理再论:随机变量Z是n个事件的随机变量取均值的一个东西,一定要先明白大数定理的前提条件:n次事件独立同分布,然后有了独立这个条件那么方差和均值的的式子就可以进行推导了,然后当n趋近于无穷的时间就有了结论:方差趋近于零,随机变量Z的值都收敛于均值,因为随机性已经趋近于零了!
5.条件期望的定义
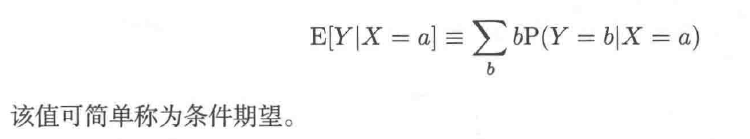

6.最小二乘法




所以说,最小二乘的最优模型就是条件概率的期望!
7.条件方差

第四章:连续值的概率分布
1.概率密度函数和概率分布函数

通过概率密度求解概率:
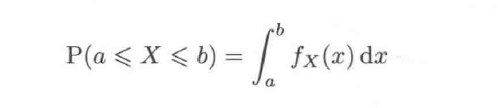
2.均匀分布

3.概率密度函数的变量变换
基本思路:求Y = 3X+2 的 f(Y)概率密度函数,已知f(X),先求出F(Y)的概率密度分布函数,在对分布函数求导即可!
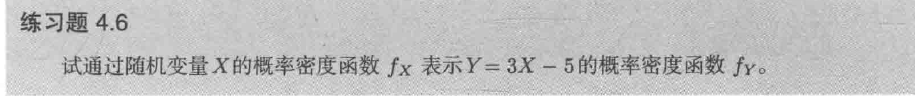



4.联合概率分布和联合概率密度函数



5.离散值到实数域上的推广:

练习题:

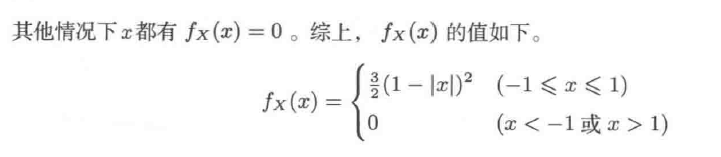
6.连续型随机变量的期望:



7.连续型随机变量的方差和标准差


8.正态(高斯)分布与中心极限定理
正态分布定义:



正态分布的一些注意点和一些性质:


中心极限定理:
正态分布处处皆在一种说法:是由误差的叠加引起的;
如果初始条件相同,通过无数的误差叠加后,最终将接近正态分布!(是符合常理的,绝大多数人都是相差不多的,两边的就是比较特殊的人群,其实就是这个道理!)



中心极限定理其实就是先假设事件都是独立同分布(大数定理也是相同的假设),然后当事件达到一定数量后经过误差的不断累积,最终的随机变量服从正态分布!
第五章:协方差矩阵、多元正态分布与椭圆
1.协方差与相关系数
协方差的定义:

协方差的性质:


相关系数的定义:
协方差的值,对不同值域的随机变量之间,不好度量,而且平方项也容易溢出,
我们的目的只是想要度量两个随机变量的相关性,就引出了相关系数,对协方差的的值进行归一化即可!


相关系数的性质:


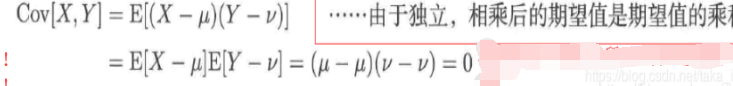
协方差与相关系数的局限性:
对于数据的分析不能仅凭借相关系数的值来判定,当值为1的时候不一定就是有关的(可能是由于某种客观原因造成
的这种现象);当值为0的时候不一定就没有关系,可能他是很有规则的椭圆,圆形等等!
2.协方差矩阵
协方差矩阵的定义:







这些矩阵的运算,全部可以当成标量进行处理,因为标量组成了向量,就是特殊到一般的一个过程!
形象很抽象,但是缘由很简单!
协方差矩阵的变量变换:



3.多元正态分布
标准的多元正态分布(形成的条件必须是:独立同分布+标准的正态分布):



一般的多元正态分布(对标准的多元正态分布进行变换)(方差就是协方差矩阵表示):


对标准多元正太分布进行变换:
(引出一般多元正态分布的协方差矩阵对角化问题)
先对标准的多元正态分布乘对角阵D进行放缩变换,在乘以一个正交矩阵进行旋转变换!

得到经过放缩和旋转变换的Y分布为一般的多元正态分布。
发现该式子的结果是一个协方差矩阵,但是没有进行对角化,(不满足独立同分布的一般多元正态分布)
可以通过变换:通过对称矩阵V(协方差矩阵)和正交矩阵Q实现对角化结果D的平方开根号!就实现了对角化!



来一道练习题:


最后是对随机变量Z的变换,所以是不带平方的!
多元正态分布的概率密度函数:



多元正态分布的性质:




截面(条件分布):

投影(边缘分布):




4.协方差矩阵与椭圆的关系


绘制椭圆假设是二元的正态分布,就是一个椭圆,绘制多个二元的正态分布不就是协方差矩阵嘛!

所以说,协方差矩阵就是多个椭圆组成的等高线图!
第六章:估计与检验
1.描述样本分布情况
均值,方差:我们经常用来,描述样本的分布情况,但是缺点是容易受到离群点的影响。
中位数:由于算的是样本的个数,所以对离群点更加鲁棒一些。
四分位数:在中位数的两个序列上,在进行中位数的分割,得到三个分为点,25%,50%,75%,通常来衡量样本分布是否对称
第七章:伪随机数
随机数序列:满足独立同分布的随机变量序列X1,X2.....称为随机数序列。
伪随机数序列:


三角形内的均匀分布:

在三角形区域内就接受,不在就拒绝,当样本数足够大就可以得到均匀分布,但是这并不是最佳解法!
可以通过线性变换的手段,变为一个好求的区间,额.....