蚁群算法基本原理:
背景: 在自然界中,生物群体所表现出的智能得到越来越多的关注,许多的群智能优化算法都是通过对群体智能的模拟而实现的。其中模拟蚂蚁群体觅食的蚁群算法成为一种主要的群智能算法。
算法原理:
在自然界中,对于觅食的蚂蚁群体,其可以在任何和没有提示的情况下找到食物和巢穴之间的最短路径。并且能够根据和环境的变迁,自适应地找到新的最优路径。根据生物学家研究,蚂蚁群体这一行为的根本原因是:蚂蚁在寻找食物的过程中,能在其走过的路径上释放一种特殊的物质----信息素,随着时间的推移,这种信息素会逐渐地挥发,而对于后来的蚂蚁,选择某条路径的概率与该路径上信息素的浓度成正比。当某一条路径上通过的蚂蚁越多的时候,这条路径上的信息素的浓度就会累积越大,后来的蚂蚁选择此路径的概率也就越大。路径上蚂蚁越多,导致信息素浓度越高,从而会吸引更多的蚂蚁,从而形成一种正反馈机制,通过这种机制,最终蚁群可以发现最短路径。
真实蚁群觅食过程:
在觅食的初始阶段,环境中没有信息素,所以蚂蚁选择哪条路径完全是随机的。之后选择路径就会受到信息素的影响。这里需要说明的时是,信息素是一种生物体内分泌的化学物质,会随着时间的推移而挥发,如果每只蚂蚁在单位距离上留下的信息素浓度相同,则对于越短的路径,信息素的残留浓度就会越高,这被后来的蚂蚁选择的概率也就越大。而经过的蚂蚁越多,由于群体中的正反馈机制,路径上信息素的浓度也就越大,最终会导致整个蚁群寻找到最短路径。
举个栗子:
如下图所示:

假设从A点到B点,A,B之间的距离一定,有三条路径可选。
初始时每条路径分配一只蚂蚁,记为1,2,3,假设L(ACB)=2*L(ADB), L(AEB)=3*L(ADB),所有蚂蚁的行走速度相同。假设蚂蚁沿着ADB从A到B,需要4个单位时间;所以在t取不同值的时候:
t=4:
蚂蚁1到达D, 蚂蚁2走到一半路程,蚂蚁3走了三分之一的路程
t=8:
蚂蚁1返回A, 蚂蚁2到达B,蚂蚁3走了三分之二的路程
.....
t=48:
蚂蚁1往返于AB之间6次, 蚂蚁2往返于AB间3次,蚂蚁3往返于AB间2次
在不考虑信息素挥发的条件下:
三条路径上信息素浓度之比:D(ADB):D(ACB):D(AEB)=6:3:2
按照蚁群寻找路径的正反馈机制:按照信息素的指导,蚁群在路径ADB上指派6只蚂蚁,在路径ACB上指派3只蚂蚁,在路径AEB上指派2只蚂蚁.
若继续寻找,则按照正反馈机制,最终所有蚂蚁都会选择最短的路径ABD,而放弃其他两条路径。
蚁群算法数学模型的建立:
1.在对实际的蚁群进行建模的过程中,需要解决,蚁群中蚂蚁个体的建模问题,信息素的更新机制,以及整个蚁群的内部机制
a. 信息素的更新机制:
信息素的更新方式有两种,一种是挥发,也就是所有路径上的信息素以一定的比率减少。另一种是信息素的增强,给有蚂蚁走过的路径增加信息素。
b. 蚂蚁个体的建模问题:
虽然单个蚂蚁可以构造出问题的可行解,但是蚂蚁个体之间需要通过协作才能找出待优化问题的最优解或者次优解,而信息素就是蚂蚁之间进行互相协作的媒介。信息素的蒸发机制使得对过去的寻优历史有一定的遗忘度,避免使后来的蚂蚁在搜索中受到较差解的影响。
下面以TSP问题为例,给出蚁群算法的模型:
参考文献:【1】M. Dorigo, V. Maniezzo and A. Colorni, "Ant system: optimization by a colony of cooperating agents," in IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 26, no. 1, pp. 29-41, Feb. 1996.
TSP问题:
在一张地图上有n个城市,一名推销员需要不重复的一次走过n个城市进行推销,求解他按照怎样的路径,从才能使走过的距离最短。
这个问题的解法可以描述如下:
假设城市 i 的坐标坐标为
![]()
城市i,j之间的距离可以表示为:
![]()
为每只蚂蚁设置一个禁忌表,记录其走过的城市(防止重复走过城市),禁忌表中第一个位置是蚂蚁是初始时刻蚂蚁所在的城市,当所有城市都加入禁忌表的时候,表示蚂蚁走完了所有的城市,完成一次周游。令![]() 为城市i, j之间的信息素的量,初始时刻其取值为:
为城市i, j之间的信息素的量,初始时刻其取值为:
![]()
假设在(t, t+n)时刻所有蚂蚁完成一次周游,则在t+n时刻城市i, j 之间的信息素含量可以表示为:
![]()
其中:表示时间段 (t, t+n) 之间信息素的挥发系数。则
表示信息素的剩余量。挥发系数取值范围(0, 1)
表示在时间段 (t, t+n) 之间信息素的增加量,其计算方式如下所示:
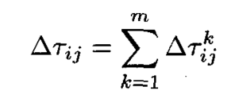
表示第k只蚂蚁在本次迭代中留在路径i, j之间的信息素的量, 计算方式如下所示(ant-cycle模型):

其中:是正常数,
表示蚂蚁k在周游中经过的路径。
原文中对参数的解释如下:

同时论文中还提到两种的计算方式:
(1)ant-density模型
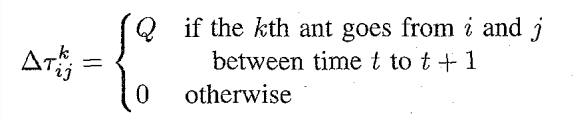
(2)ant-quantity模型:

ant-cycle模型的实际效果更好,因为他应用了全局信息更新路径上的信息素,而其他两种模型只是用了局部信息。
在t时刻, 蚂蚁k从城市i转移到城市可的概率可以由以下方式计算得到:

其中:是一个启发式因子,计算方式为:
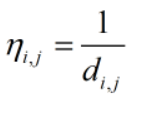
表示蚂蚁从城市i转移到城市j的期望程度。
表示在城市i处蚂蚁k可以选择走的城市的集合。
表示信息素和期望启发式因子的相对重要程度。
分析上面的公式可知:
路径i,j信息素含量越高,蚂蚁选择该路径的概率越大,而路径i.j之间的距离越大吗,启发式因子就越小,则蚂蚁选择该路径的概率就越小,蚂蚁选择路径i,j的概率与上述两个因素都有关系。
matlab代码实现:
clear all;
close all;
clc;
C = [1304 2312; % 城市坐标
3639 1315;
4177 2244;
3712 1399;
3488 1535;
3326 1556;
3238 1229;
4196 1044;
4312 790;
4386 570;
3007 1970;
2562 1756;
2788 1491;
2381 1676;
1332 695;
3715 1678;
3918 2179;
4061 2370;
3780 2212;
3676 2578;
4029 2838;
4263 2931;
3429 1980;
3507 2376;
3394 2643;
3439 3201;
2935 3240;
3140 3550;
2545 2357;
2778 2826;
2370 2975];
% figure(1);
% scatter(C(:,1),C(:,2),'k','d');
% title('城市分布图');
[M,N] = size(C);
% M为问题的规模 M个城市
distance = zeros(M,M); % 用来记录任意两个城市之间的距离
% 求任意两个城市之间的距离
for m=1:M
for n=1:M
distance(m,n) = sqrt(sum((C(m,:)-C(n,:)).^2));
end
end
m = 50; % 蚂蚁的个数 一般取10-50
alpha = 1; % 信息素的重要程度 一般取【1,4】
beta = 5; % 启发式英子的重要程度 一般取【3,5】
rho = 0.25; % 信息素蒸发系数
G = 150;
Q = 100; % 信息素增加系数
Eta = 1./distance; % 启发式因子
Tau = ones(M,M); % 信息素矩阵 存储着每两个城市之间的信息素的数值
Tabu = zeros(m,M); % 禁忌表,记录每只蚂蚁走过的路程
gen = 1;
R_best = zeros(G,M); % 各代的最佳路线
L_best = inf.*ones(G,1); % 每一代的最佳路径的长度 初始假设为无穷大
% 开始迭代计算
while gen<G
% 将m只蚂蚁放到n个城市上
random_pos = [];
for i=1:(ceil(m/M)) % m只蚂蚁随即放到M座城市
random_pos = [random_pos,randperm(M)]; % random_pos=[1~31 + 1~31] 将每只蚂蚁放到随机的城市 在random_pos 中随机选择m个数,代表蚂蚁的初始城市
end
Tabu(:,1) = (random_pos(1,1:m))'; % 第一次迭代每只蚂蚁的禁忌表
for i=2:M % 从第二个城市开始
for j=1:m % 每只蚂蚁
visited = Tabu(j,1:(i-1)); % 在访问第i个城市的时候,第j个蚂蚁访问过的城市
% visited=visited(1,:);
unvisited = zeros(1,(M+1-i)); % 待访问的城市
visit_P = unvisited; % 蚂蚁j访问剩下的城市的概率
count = 1;
for k=1:M % 这个循环是找出未访问的城市
if isempty(find(visited==k)) %还没有访问过的城市 如果成立。则证明第k个城市没有访问过
unvisited(count) = k;
count = count+1;
end
end
% 计算待选择城市的概率
for k=1:length(unvisited) % Tau(visited(end),unvisited(k))访问过的城市的最后一个与所有未访问的城市之间的信息素
visit_P(k) = ((Tau(visited(end),unvisited(k)))^alpha)*(Eta(visited(end),unvisited(k))^beta);
end
visit_P = visit_P/sum(visit_P); % 访问每条路径的概率的大小
% 按照概率选择下一个要访问的城市
% 这里运用轮盘赌选择方法 这里也可以选择选择概率最大的路径去走, 这里采用轮盘赌选择法。
Pcum = cumsum(visit_P);
selected = find(Pcum>=rand);
to_visited = unvisited(selected(1));
Tabu(j,i) = to_visited; % 添加到禁忌表
end
end
if gen>=2
Tabu(1,:) = R_best(gen-1,:);
end
% 记录m只蚂蚁迭代的最佳路线
L = zeros(1,m);
for i=1:m
R = Tabu(i,:);
L(i) = distance(R(M),R(1)); % 因为要走一周回到原来的地点
for j=1:(M-1)
L(i) = L(i)+distance(R(j),R(j+1));
end
end
L_best(gen) = min(L); % 记录每一代中路径的最短值
pos = find(L==L_best(gen));
R_best(gen,:) = Tabu(pos(1),:); % 最优的路径
% 更新信息素的值
Delta_Tau = zeros(M,M);
for i=1:m % m只蚂蚁
for j=1:(M-1) % M座城市
Delta_Tau(Tabu(i,j),Tabu(i,j+1)) = Delta_Tau(Tabu(i,j),Tabu(i,j+1)) + Q/L(i); % m只蚂蚁的信息素累加 这里采用的是论文中ant-cycle模型
end
Delta_Tau(Tabu(i,M),Tabu(i,1)) = Delta_Tau(Tabu(i,M),Tabu(i,1)) + Q/L(i);
end
Tau = (1-rho).*Tau+Delta_Tau; % 更新路径上的信息素含量
% 禁忌表清零
Tabu = zeros(m,M);
for i=1:(M-1)
plot([C(R_best(gen,i),1),C(R_best(gen,i+1),1)],[C(R_best(gen,i),2),C(R_best(gen,i+1),2)],'bo-');
hold on;
end
plot([C(R_best(gen,n),1),C(R_best(gen,1),1)],[C(R_best(gen,n),2),C(R_best(gen,1),2)],'ro-');
title(['最短路径:',num2str(L_best(gen))]);
hold off;
pause(0.05);
gen = gen+1;
end
figure(2);
plot(L_best);
title('路径长度变化曲线');
xlabel('迭代次数');
ylabel('路径长度数值');运行结果:


最优路径相同,只是起点不一样。

