一因子载荷矩阵A的估计方法

1. 主成分分析法

祥见【因子分析 factor analysis (一 )：模型的理论推导】https://blog.csdn.net/qq_29831163/article/details/88901245

2. 极大似然估计法（略）

3. 主因子法

$\large A=\left [\sqrt{\lambda _{1}^{*}} u_{1}^{*} \sqrt{\lambda _{2}^{*}} u_{2}^{*} ...\sqrt{\lambda _{p}^{*}} u_{p}^{*} \right ]$

主因子方法是对主成分方法的修正，假定我们首先对变量进行标准化变换。则 $\large R=AA^{T}+D ;$ $\large R^{*}=AA^{T}=R-D$ ;称 $\large R^{*}$ 为约相关系数矩阵， $\large R^{*}$ 对角线上的元素是 $\large h_{i}^{2}$ ，而不是1。

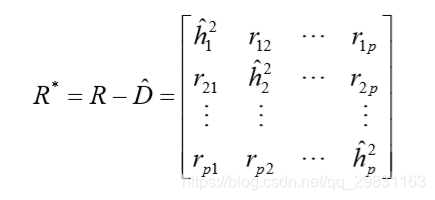
直接求 $\large R^{*}$ 的前 p 个特征值和对应的正交特征向量。得到如下的矩阵

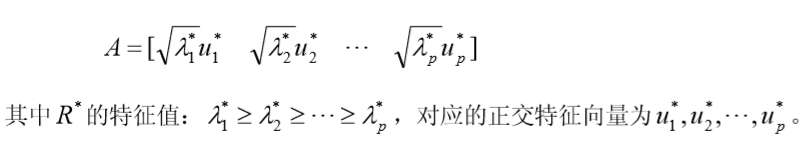
在实际应用中，特殊因子的方差一般都是未知的，可以通过一组样本来估计。估计的方法有如下几种：

1）取 $\large h_{i}^{2} =1$ ，在这个情况下主因子解与主成分解等价。
2）取 $\large h_{i}^{2} =R_{i}^{2}$ ， $\large R_{i}^{2}$ 为 $\large x_{i}$ 与其它所有的原始变量 $\large x_{j}$ 的复相关系数的平方，即 $\large x_{i}$ 对其余的 p-1个 $\large x_{j}$ 的回归方程的判定系数，这是因为 $\large x_{j}$ 与公共因子的关系是通过其余的 p-1 个 $\large x_{j}$ 的线性组合联系起来的。

3) 取 $\large h_{i}^{2 }=max\left |r_{ij} \right |\left ( j\neq i \right )$ ，这意味着取 $\large x_{i}$ 与其余的 $\large x_{j}$ 的简单相关系数的绝对值的最大值。

4）取 $\large \hat{h_{i}^{2}}= \frac{1}{p-1}\sum_{j=1; j\neq i}^{p}r_{ij}$ ，其中要求该值为正数。

5）取 $\large h_{i}^{2}=\frac{1}{r^{ii}}$ ，其中 $\large r^{ii}$ 是 $\large R^{-1}$ 的对角元素。

二试用主成分分析法求因子分析模型

例1 假定某地固定资产投资率 $\large x_{1}$ ，通货膨胀率 $\large x_{2}$ ，失业率 $\large x_{3}$ ，相关系数矩阵为 $\large \begin{bmatrix} 1&\frac{1}{5} & -\frac{1}{5}\\ \frac{1}{5}& 1& -\frac{2}{5} \\ -\frac{1}{5}& -\frac{2}{5} & 1 \end{bmatrix}$

计算的MATLAB程序为：

clc,clear 
r=[1 1/5 -1/5;1/5 1 -2/5;-1/5 -2/5 1]; 
[vec,val,con]=pcacov(r);num=2; 
f1=repmat(sign(sum(vec)),size(vec,1),1); 
vec=vec.*f1;     %特征向量正负号转换 
f2=repmat(sqrt(val)',size(vec,1),1); 
a=vec.*f2   %载荷矩阵 
s1=sum(a.^2,1) 
tt=a.^2;tt=tt(:,1:num); 
s2=sum(tt,2)

三用主因子分析法求因子分析模型

例2 假定某地固定资产投资率 $\large x_{1}$ ，通货膨胀率 $\large x_{2}$ ，失业率 $\large x_{3}$ ，相关系数矩阵为 $\large \begin{bmatrix} 1&\frac{1}{5} & -\frac{1}{5}\\ \frac{1}{5}& 1& -\frac{2}{5} \\ -\frac{1}{5}& -\frac{2}{5} & 1 \end{bmatrix}$

因子分析 factor analysis (三) ：因子载荷矩阵的估计方法

一因子载荷矩阵A的估计方法

1. 主成分分析法

2. 极大似然估计法（略）

3. 主因子法

二试用主成分分析法求因子分析模型

三用主因子分析法求因子分析模型

猜你喜欢

因子分析 factor analysis (三) ： 因子载荷矩阵的估计方法

一 因子载荷矩阵A的估计方法

1. 主成分分析法

2. 极大似然估计法（略）

3. 主因子法

二 试用主成分分析法求因子分析模型

三 用主因子分析法求因子分析模型

猜你喜欢

因子分析 factor analysis (三) ：因子载荷矩阵的估计方法

一因子载荷矩阵A的估计方法

二试用主成分分析法求因子分析模型

三用主因子分析法求因子分析模型