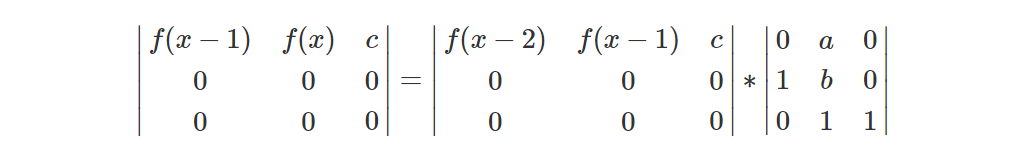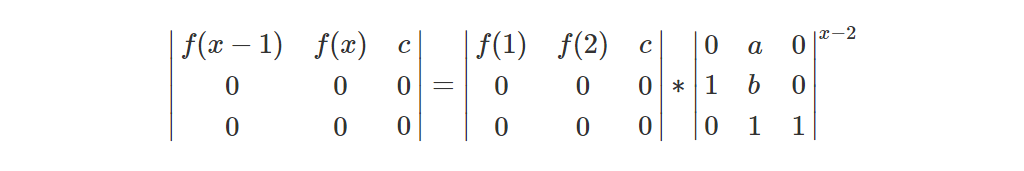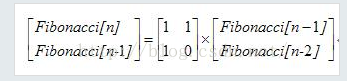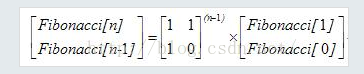Description
A number sequence is defined as follows:
f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.
Given A, B, and n, you are to calculate the value of f(n).
The input consists of multiple test cases. Each test case contains 3 integers A, B and n on a single line (1 <= A, B <= 1000, 1 <= n <= 100,000,000). Three zeros signal the end of input and this test case is not to be processed.
Output
For each test case, print the value of f(n) on a single line.
1 1 3
1 2 10
0 0 0
2
5
题意:
题意很简单就是给你一个数n,让你求F(n)
分析:
网上有很多博客上写找规律,找循环节,但是当你们问他为什么这个周期是这些,却很难回答。如果它真的具有规律并具有固定周期,一定可以通过某种方法证明,只不过我们不会,但对于这个题目应该是没法证明的,看HDU的discuss中就给了下面几组测试数据。
input
247 602 35363857
376 392 9671521
759 623 18545473
53 399 46626337
316 880 10470347
0 0 0
output
4
3
5
2
3
这几组测试数据如果去验证所谓规律AC的代码,有几个实际上是不对的
因此考虑到斐波那契数列的性质,这个题和斐波那契数列很类似,发现我们应该使用矩阵快速幂来做,矩阵很小,模板直接写。
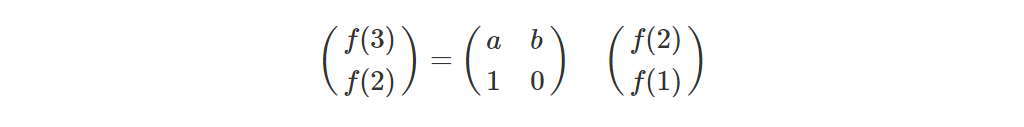
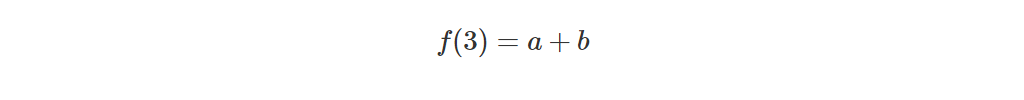
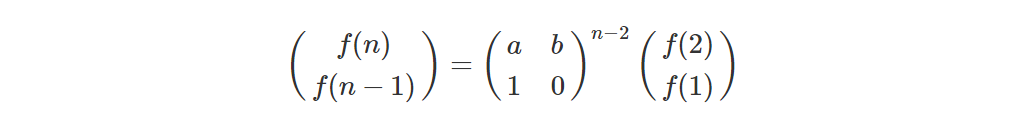
设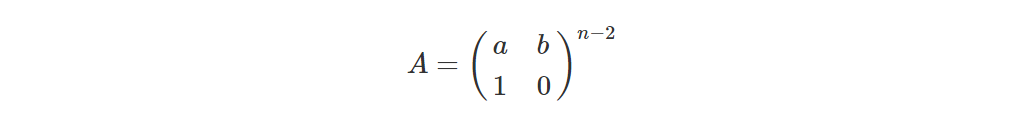
那么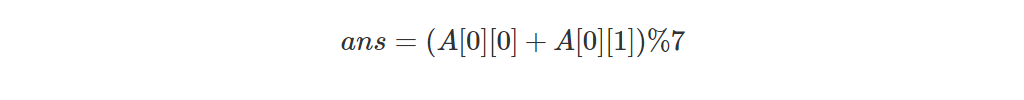
对于 ,
,
n为偶数时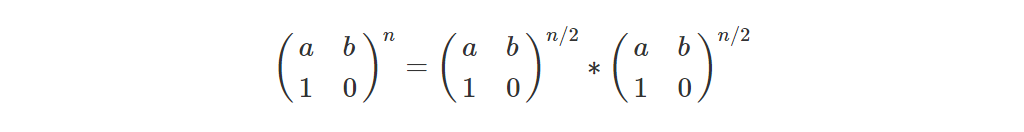
n为奇数时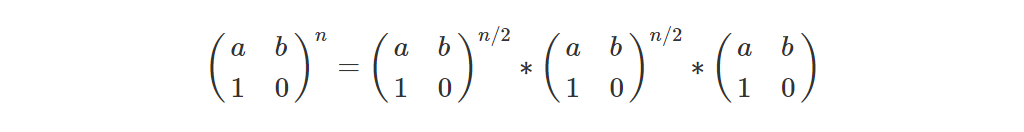
#include <bits/stdc++.h>
using namespace std;
struct Matrix
{
int m[2][2];
};
Matrix mul(Matrix a,Matrix b)
{
Matrix ans;
for(int i = 0; i < 2; i++)
{
for(int j = 0; j < 2; j++)
{
ans.m[i][j] = 0;
for(int k = 0; k < 2; k++)
{
ans.m[i][j] = (ans.m[i][j] + a.m[i][k] * b.m[k][j] % 7) % 7;
}
}
}
return ans;
}
int main()
{
int A,B,n;
while(scanf("%d%d%d",&A,&B,&n) != EOF)
{
if(A == 0 && B == 0 && n == 0) break;
if(n==2||n==1)
{
printf("1\n");
continue;
}
Matrix a,ans;
a.m[0][0] = A;
a.m[0][1] = B;
a.m[1][0] = 1;
a.m[1][1] = 0;
ans.m[0][0] = ans.m[1][1] = 1;
ans.m[0][1] = ans.m[1][0] = 0;
n -= 2;
while(n)
{
if(n & 1)
{
ans = mul(ans,a);
}
/*
&是位与操作符,n&1,是将n的二进制形式与00000000 00000001按位做与操作,这时,只要n的最右边一位是1,结果就不是0,为true,条件成立。所以这句话实际上就是if(n%2==1)
当n是奇数的时候,一开始就要进入if判断,乘了一次矩阵a,n是偶数的话,就不会乘这一次矩阵a。然后利用二分的思想进行矩阵相乘。
*/
n >>= 1;
a = mul(a,a);
}
printf("%d\n",(ans.m[0][0] + ans.m[0][1]) % 7);
}
return 0;
}
我们再通过几个例子加深理解 矩阵乘法与递推式之间的关系:(做这种题重点就在通过递推关系构造矩阵)
①斐波那契 f[i] = 1*f[i-1]+1*f[i-2]
则可以补充为:
f[i] = 1*f[i-1]+1*f[i-2]
f[i-1] = 1*f[i-1] + 0*f[i-2];
即
所以
就这两幅图完美诠释了斐波那契数列如何用矩阵来实现。
如果求f(4)比较简单直接一项一项的递推就行,若求f(10000000000),就会超时,而构造矩阵用快速幂就比较快,O(logN) 的复杂度大大降低了时间
②f(x)=a*f(x-2)+b*f(x-1)+c
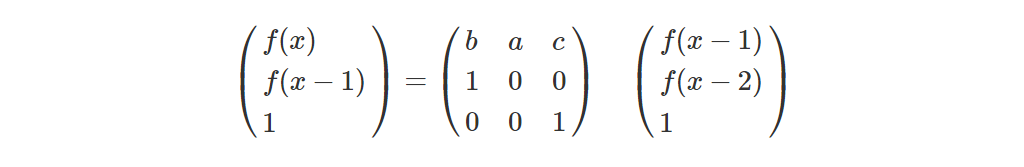
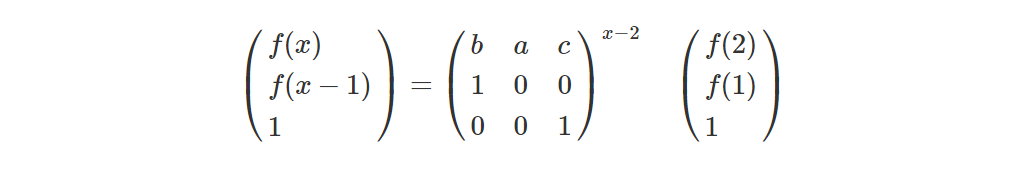
其他博主这样构造: