ML-感知机及其matlab实现

1. 感知机原理：

感知机是二分类的线性模型，其输入是实例的特征向量，输出的是事例的类别，分别是+1和-1，属于判别模型。
假设训练数据集是线性可分的，感知机学习的目标是求得一个能够将训练数据集正实例点和负实例点完全正确分开的分离超平面。如果是非线性可分的数据，则最后无法获得超平面。
感知机从输入空间到输出空间的模型如下：
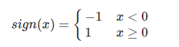
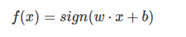
损失函数的优化目标是期望使误分类的所有样本，到超平面的距离之和最小。所以损失函数定义如下：

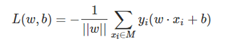
不考虑1/(||w||)，就得到感知机模型的损失函数：
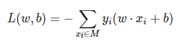
为什么忽略1/(||w||)呢？网上有人说1/(||w||)是个定值，但是个人觉得平面不唯一，这个值肯定也会变。通过参考他人观点结合思考，我觉得原因可以列为以下两点。
1）1/(||w||)不影响yi(w⋅xi+b)正负的判断，即不影响学习算法的中间过程。因为感知机学习算法是误分类驱动的，这里需要注意的是所谓的“误分类驱动”指的是我们只需要判断−yi(w⋅xi+b)的正负来判断分类的正确与否，而1/(||w||)并不影响正负值的判断。所以1/(||w||)对感知机学习算法的中间过程可以不考虑。
2）1/(||w||)不影响感知机学习算法的最终结果。因为感知机学习算法最终的终止条件是所有的输入都被正确分类，即不存在误分类的点。
综上所述，即使忽略1/(||w||)，也不会对感知机学习算法的执行过程产生任何影响。反而还能简化运算，提高算法执行效率。

2. 感知机学习算法：
感知机学习算法是对上述损失函数进行极小化，求得w和b。但是用普通的基于所有样本的梯度和的均值的批量梯度下降法（BGD）是行不通的，原因在于我们的损失函数里面有限定，只有误分类的M集合里面的样本才能参与损失函数的优化。所以我们不能用最普通的批量梯度下降,只能采用随机梯度下降（SGD）。目标函数如下：
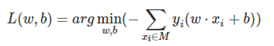
在这里插入图片描述
输入：训练数据集T。
输出：w和b；感知机模型f(x)=sign(w⋅x+b)。
更新：判断该数据点是否为当前模型的误分类点，即判断若yi(w⋅xi+b)<=0则更新：

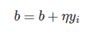
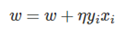
3. Matlab代码
1.感知机代码：

    function perceptron(data)
      X=data(:,[1,2]); 
      y=data(:,3);
      m=size(X,1);       
      plotData(X,y);      
     axis([-4 4 -4 4]);
      hold on
      x1=-4:0.2:4; 
      W=[0;0];   
      b=0;
      alph=1; 
      error=1;

   
    while error>0
        error=0;
       for i=1:m
          if (((W'*X(i,:)'+b)*y(i))<=0)
              error=error+1;
               W=W+alph*y(i)*X(i,:)';
               b=b+alph*y(i);
               y1=(-W(1)*x1-b)/W(2);
               plot(x1,y1,'-b');
               pause(0.5);
           end
       end
       
    end
plot(x1,y1,'-r','Linewidth',3);
  end

获得线性可分数据集代码：

function [sample]=generate_sample(step,error)
aa=0.5;
bb=2;
b1=0.3;
rr =error;
s=step;
x1(:,1) = -4:s:4;
n = length(x1(:,1));
x1(:,2) = aa.x1(:,1) + bb + b1 + rrabs(randn(n,1));
y1 = -ones(n,1);
x2(:,1) = -4:s:4;
x2(:,2) = aa.x2(:,1) + bb - b1 - rrabs(randn(n,1));
y2 = ones(n,1);
figure;
plot(x1(:,1),x1(:,2),‘bx’,x2(:,1),x2(:,2),‘k.’);
feature=[x1 y1];
category=[x2 y2];
sample=[feature;category];

绘制数据集代码：

function plotData(X,y)
   figure;
   hold on;
   pos=find(y==1);
   neg=find(y==-1);  
   plot(X(pos,1),X(pos,2),'k+','Linewidth',2,'MarkerSize',9);
   plot(X(neg,1),X(neg,2),'ko','MarkerFaceColor','r','Linewidth',2,'MarkerSize',7);
   hold off;
   end

4. Matlab仿真

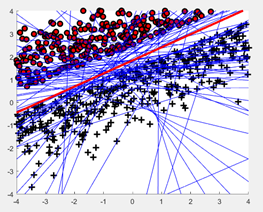
生成大小为20的线性可分数据集，绘制（x，y）以及平面上的目标函数f。如图：不同的方式标记了不同类别，迭代次数如图蓝线条个数，目标函数如红线所示。（学习率n = 1）
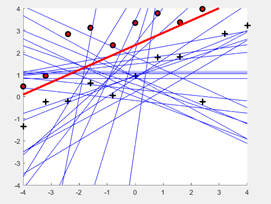
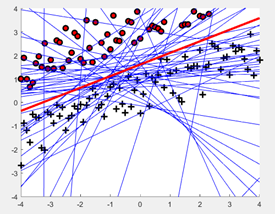
将算法运行在大小为为100和1000的线性可分数据集。如图：不同的方式标记了不同类别，迭代次数如图蓝线条个数，目标函数如红线所示。（学习率n = 1）

在这里插入图片描述

ML-感知机及其matlab实现

猜你喜欢