机器学习的科学可行性——计算学习理论

首先插句题外话，机器学习中有一条著名的定理：NO Free Lunch Theorem（NFL）。
假定我们所要训练的机器学习模型事先是没有目标任务的，也就是说这个模型针对的是出现机会均相同的“问题”（学习任务），那么任意算法模型得到的期望性能都是相同的 —— 如果我们采用的是“瞎猜”的算法，和采用其它高级算法的期望性能是一样的。（证明略）
然而，实际应用中，目标任务的出现概率不可能是均等的（需要学习的真实目标函数不满足均匀分布），也就是说我们所要训练的模型是针对特定目标任务，解决特定问题的。
所以NFL定理说明，脱离具体的应用目标任务，无法判定算法模型的优劣。
PS：机器学习算法在学习过程中对某个hypothesis是有归纳偏好的，否则就会出现这个模型对某一样例时而判为正例时而判为反例的情况。类比一个可能不太准确的例子，“薛定谔的猫”——猫在密室中是又死又活的叠加态，当观察者打开密室的那一刻波函数坍缩，猫的状态是一个确定的状态（要么死要么活）；解决某一特定问题满足条件的hypothesis可能有很多，当选用特定算法后，只有一种hypothesis会得到算法“青睐”（bias）。因此算法的归纳偏好是否与问题本身匹配，大多数情况下直接决定了算法能否取得好的性能。

一、PAC（Probably Approximately Correct）可学习

西瓜书中给出的定义为：对任意0<ε, δ<1（ε为可容忍误差，δ为置信度），所有目标概念c∈概念类C和分布D，若存在某学习算法，其输出假设h∈假设空间Η，满足

P (E (h) \leq ε) \geq 1 - δ

$P(E(h) \leqε)\geq1-δ$
则称该学习算法能从假设空间H中PAC辨识概念类C（标签），即概念类C是PAC可学习的。

二、测试误差与训练误差的关系——hoeffding不等式

很多人对机器学习抱有这样一种顾虑 —— “是否可以相信已学习好的模型在实际应用中得出的结果？”
除了近年来在某些领域超越人类表现的应用实例外，基础计算学习理论也对其科学可行性提供了有说服力的保障。

1.有限假设空间（Finite hypothesis space）

首先对假设空间做一解释：针对某目标任务（Ground Truth）有很多假设模型（hypothesis）可以解决它，而机器学习的目标就是学习到最接近Ground Truth 的 hypothesis（既匹配训练样本空间（目标任务空间的独立同分布采样），又有较强的泛化能力。即可以较好匹配某目标任务的无限全集空间）。这些假设模型的集合就称为假设空间。

机器学习的目标并不是在已知的训练样本空间有好的表现，而是在未知的测试样本空间有好的表现，即较强的泛化能力。
因此，在有限假设空间中，根据Hoeffding不等式，上述目标可描述为：

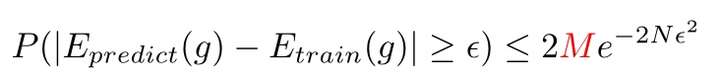
这里写图片描述

其中， $E_{predict}(g)$ 为测试样本误差， $E_{train}(g)$ 为训练样本误差，ε为可容忍误差，M为假设空间的大小，N为采样的训练样本数。
这个公式表明，当训练样本数足够大时在测试样本集上的表现可以以非常小的误差接近在训练样本集上的表现。即对于该目标任务是PAC可学习的。
换句话说，对于一个训练样本空间足够大，且在训练样本集上表现非常好的机器学习模型来说，我们完全可以相信它在未知测试样本集上的表现也是很不错的。

2.无限假设空间（Infinite hypothesis space）

在现实学习任务中通常面临的是无限假设空间。对于无限假设空间需要引入VC维的概念。
不过在此之前需要先介绍其他几个概念：
对分（Dichotomy）：对于二分类问题来说，假设空间中的假设对某样本集的每种可能的判定结果（正例，反例）称为对该样本集的一种对分。如下图所示，

N=1时
N=1

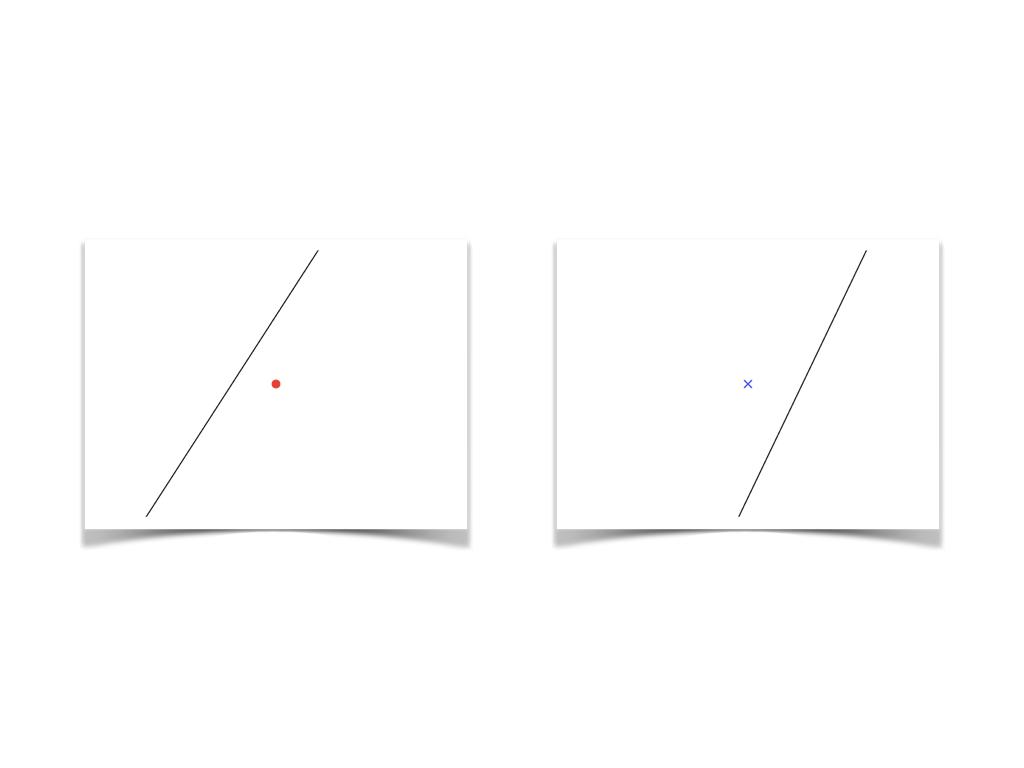
N=2时
N=2
增长函数（Growth function）：
$这里写图片描述$
增长函数表示了假设空间H对N个样例所能判定（标记）的最大可能结果数。描述了假设空间的表示能力，反映出假设空间的复杂度。由此可以看出假设空间的表示能力与其复杂度是一对矛盾的属性。
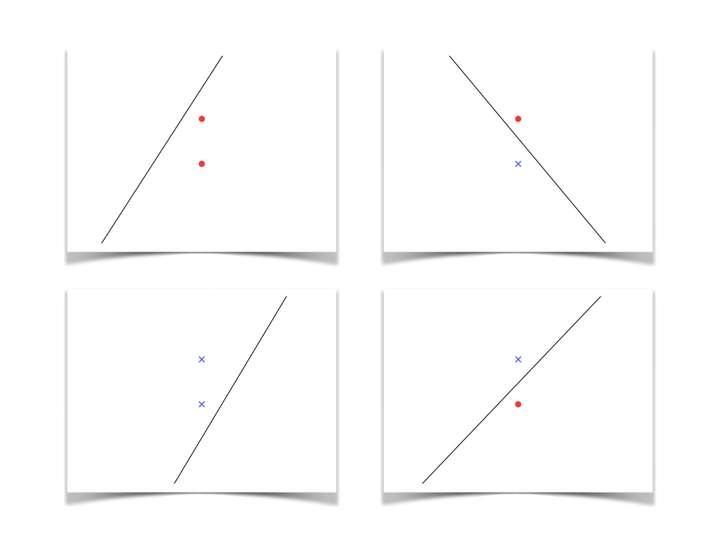
如下图所示，当样例样本数N=3时，会出现两种情况,

N=3 时(1)
N=3

N=3时 (2)
N=3
图N=3 (1)对3个样例的对分可能结果有8种，而图N=3 (2)的对分可能结果只有6种，然而根据增长函数的定义可知，假设空间对3个样例所能判定的最大可能结果数是8。因此当N=3时，增长函数 $m_H(N)=8$
由此我们可以看出，尽管对于无限假设空间，其中包含了无限个假设，但是其增长函数却是有限的。

打散（Shatter）：若假设空间H能实现样例集D上的所有对分，即 $m_H(N)=2^N$ ，则称样例集D能被假设空间H打散。例如N=1,2,3

下面就要介绍VC维的概念了：
VC维（Vapnik-Chervonenkis dimension）：假设空间H的VC维是能被H打散的最大样例集的大小，即

V C (H) = m a x {N ： m_{H} (N) = 2^{N}}

$VC(H) = max\{N：m_H(N) = 2^N\}$
由定义可以看出VC维与目标任务数据的分布无关，因此在数据分布未知时仍能得出假设空间的VC维。
如下图所示，当N=4时，只能对分得14个结果，下面两种情况无法实现对分：

N=4时
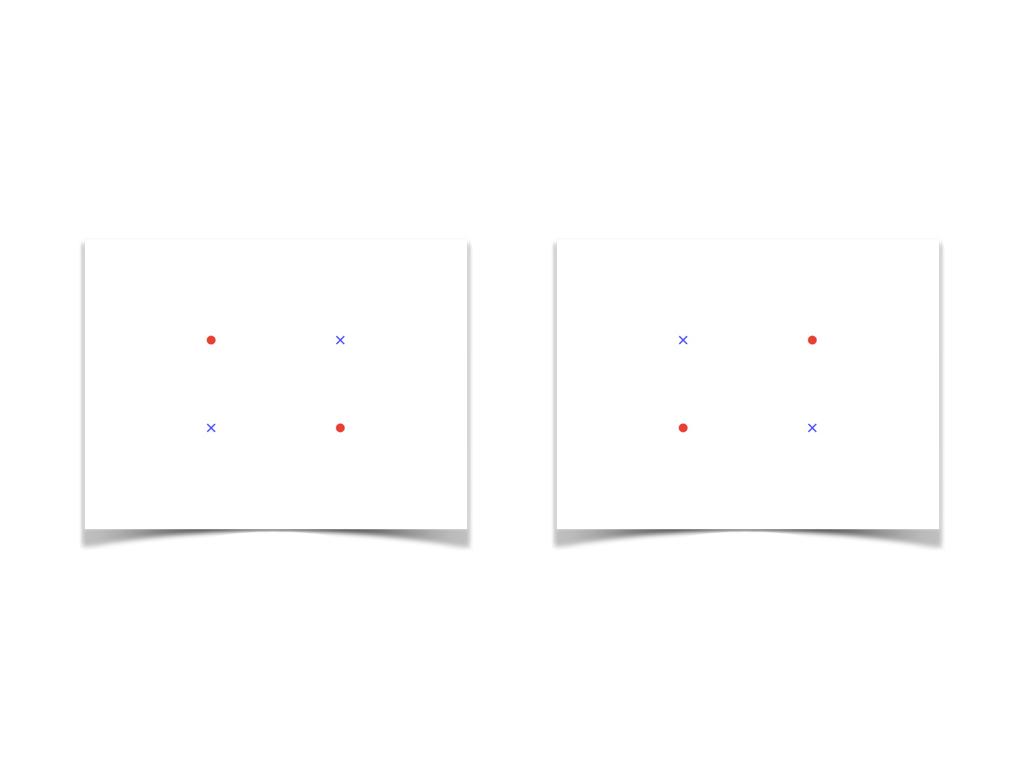
这里写图片描述
因此上述情况的假设空间H的VC维是3（N=4时无法被打散）

到这里我们就可以得出无限假设空间的Hoeffding不等式了：
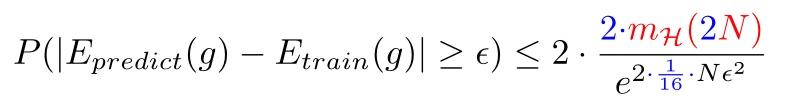
这里写图片描述
即

不等式右边就称为VC界（VC bound）
由此可以看出，在无限假设空间中，只要训练样本集足够大，机器学习模型在未知测试样本集上的表现可以无限接近其在训练样本集上的表现。

我们之前提到过假设空间的表示能力与其复杂度是一对矛盾的属性，换句话说就是VC维越大，模型的表示能力越强，与此同时样本复杂度就越高。

测试误差与训练误差的关系：
这里写图片描述
由上式可以看出，VC维越小，测试误差就会越接近训练误差；而VC维越大，模型的表达能力就越强，对训练样本的拟合就越好，从而训练误差就越小。
所以，在机器学习算法的实际应用中，合适的VC维选择对学习模型的最终效果也有重要的影响。

参考资料：
1.《机器学习》周志华著
2.写给大家看的机器学习书

推荐阅读：
《智能时代》吴军著