Jzoj P5231 序列问题___分治+思维+前缀和

版权声明：欢迎借鉴，谢绝抄搬。 https://blog.csdn.net/Gx_Man_VIP/article/details/86682197

题目大意：

$n<=500000,0<=A[i]<=10^9$

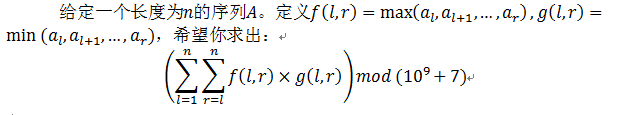
分析：

显然直接枚举区间时间复杂度为 $O(n^2)$，不能接受
那么我们可以考虑分治，
那么区间 $[1,n]$就会被分成多块
即 (以下 $/2$均为向下取整)
$[1,n]$
$[1,(n+1)/2]$, $[(n+1)/2+1,n]$
…
$[1,1]$, $[2,2]$,…, $[n,n]$
那么我们可以发现如果要使得不重复计算贡献的话，
一个区间 $[l,r]$的总贡献为
所有过其中点 $mid$且任一端点不为 $mid$的子区间的( $区间max*min$)之和
即 $[l,mid+1],[l,mid+2],...,[l,r]$的，
$[l+1,mid+1],[l+1,mid+2],...,[l+1,r]$的，
…
$[mid-2,mid+1],[mid-2,mid+2],...,[mid-2,r]$的，
$[mid-1,mid+1],[mid-1,mid+2],...,[mid-1,r]$的区间 $max*min$之和

对于一段区间 $[l,r]$的贡献求解方面，
设
$max_i$表示 $[mid+1,i]$中 $a_i$的最大值( $i＞mid$)
$min_i$同理求最小值
$summax_i$表示 $max_i$在 $[mid+1,i]$的和
$summin_i$同理表示 $min_i$的
$sumcj_i$表示 $max_i*min_i$在 $[mid+1,1]$的和
这些可以在 $O(r-mid)$内处理完
然后我们枚举左端点 $L$， $L$从 $mid-1$开始
$cmax$为 $[L,mid]$中 $max(a_i)$
$cmin$为 $[L,mid]$中 $min(a_i)$
另设
$p$为 $[mid+1,r]$中第一个满足 $a_{p+1}<cmin$的，不存在时 $p=r$
$q$为 $[mid+1,r]$中第一个满足 $a_{q+1}＞cmax$的，不存在时 $q=r$
那么我们就可以分类讨论了，
我们钦定 $p<q$,

$①区间[mid+1,p]$：
此时并没有到 $p+1$，更没有到 $q+1$，
那么显然所有 $[L,R]$ $(R∈[mid+1,p])$的最大值和最小值都是 $cmax,cmin$,
他们的总贡献为 $cmax*cmin*(p-(mid+1)+1)$

$②区间[p+1,q]$：
此时已经经过了 $p+1$，所以 $[L,R]$ $(R∈[p+1,q])$中
因为没有到 $q+1$，所以最大值依然是 $cmax$，
但是最小值已经不在 $[l,p]$中，而应该在 $[p+1,q]$中，但是我们并不能确定每在 $[p+1,q]$中经过一个点，它的最小值是否会变，所以我们一开始就预处理了一个最小值的前缀和，
对于 $cmax*最小值_1+cmax*最小值_2...+cmax*最小值_x$而言，
就为 $cmax*最小值之和$
那么他们的总贡献为 $cmax*最小值总和$，即 $cmax*(summin_q-sum_{(p+1)-1})$

$③[q+1,r]$
此时已经经过了 $p+1$, $q+1$，所以 $[L,R]$ $(R∈[q+1,r])$中
最小值，最大值已经不取决于区间 $[L,q]$了，
此时我们就是用到一开始预处理的 $sumcj_i$了，
即贡献为 $Σ_{i=q+1}^{r}max_i*min_i(max_i,min_i此时肯定比cmax,cmin优)$
即为 $sumcj_{r}-sumcj_{(q+1)-1}$
$q<p$同理时候好像就是第二步换了一下位置

一开始用了 $O(1)$快速乘，结果常数大 $T$了 $4,5$个点。。后来发现 $longlong$炸不了，然后取模可能出现的负数要处理一下。

代码：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <queue>
#include <algorithm>

#define inf 0x7fffffff
#define N 500005

using namespace std;

typedef long long ll;	

ll maxnum[N], minnum[N], summax[N], summin[N], sumcj[N], a[N], Answer; 
int n, modn = 1000000007;

void read(ll &x)
{
	ll f = 1; x = 0; char s = getchar();
	while (s < '0' || s > '9')   { if (s == '-') f = - 1;  s = getchar(); }
	while (s >= '0' && s <= '9') { x = x * 10 + (s - '0'); s = getchar(); }
	x = x * f;
}

void Work(int l, int r)
{
	if (l == r) { Answer = ((Answer + a[l] * a[l] % modn) % modn + modn) % modn; return; }
	int mid = (l + r) >> 1; 
    Work(l, mid); Work(mid + 1, r);
	maxnum[mid] = summax[mid] = 0;
	minnum[mid] = inf, summin[mid] = 0;
	sumcj[mid] = 0;
	for (int i = mid + 1; i <= r; i++)
	{
		maxnum[i] = max(maxnum[i - 1], a[i]), summax[i] = (summax[i - 1] + maxnum[i]) % modn;
		minnum[i] = min(minnum[i - 1], a[i]), summin[i] = (summin[i - 1] + minnum[i]) % modn;
        sumcj[i] = ((sumcj[i - 1] + maxnum[i] * minnum[i] % modn) % modn + modn) % modn;
	}
	
	ll max_cdp = 0, min_cdp = inf;
	int p = mid, q = mid;
	for (int i = mid; i >= l; i--)
	{
		max_cdp = max(max_cdp, a[i]);
		min_cdp = min(min_cdp, a[i]);
		while (a[p + 1] >= min_cdp && p < r) p++;
		while (a[q + 1] <= max_cdp && q < r) q++;
		if (p < q) Answer = ((Answer + max_cdp * min_cdp % modn * (p - mid) % modn + (summin[q] - summin[p]) * max_cdp % modn + (sumcj[r] - sumcj[q])) % modn + modn) % modn;
              else Answer = ((Answer + max_cdp * min_cdp % modn * (q - mid) % modn + (summax[p] - summax[q]) * min_cdp % modn + (sumcj[r] - sumcj[p])) % modn + modn) % modn;
	 } 
}

int main()
{
	freopen("seq.in", "r", stdin); 
	freopen("seq.out", "w", stdout);
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) read(a[i]);
	Work(1, n);
	printf("%lld\n", Answer);
	return 0;
}