题解 smoj 2806 【建筑物】
- 题目描述
- 分析
- 转移
- 优化 1
- 优化2
- 优化后的DP方程
- 注意事项
- 代码

题解 smoj 2806 【建筑物】

时间：2019.3.15

==DP of DP of DP==

题目描述

有R红色立方体，G绿色立方体和B蓝色立方体。每个立方体的边长是1。现在有一个N × N的木板，该板被划分成1×1个单元。现在要把所有的R+G+B个立方体都放在木板上。立方体必须放置在单元格内，单元格可以竖立放置多个立方体。

放置在板上的立方体可以被视为“建筑物”。一个“建筑物”被称为“美丽建筑物”，当且仅当：人站在南面，向北面望过去，观察建筑物时，所有可见立方体都是相同的颜色。

例如，在下图中，左侧建筑物是“美丽建筑物”，而右侧建筑物则不是。

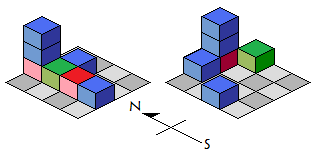
问题是：给出R，G，B，N，有多少种不同的“美丽建筑物”，答案模1000000007。

分析

数数题，考虑DP。

下文为了方便，用\(A, B, C\)来表示\(R, G, B\)

不妨钦定颜色\(A\)在前面

钦定颜色\(A\)是蓝色

设\(F(N, A, B, C)\)为前\(i\)列，三种颜色分别使用\(A, B, C\)个的方案数，

可以发现每一列都是独立的，即只要知道该列使用三种颜色的各自块数，该列的方案数就唯一确定。

设\(G(A, B, C)\)为单列使用三种颜色立方体各\(A, B, C\)个时的方案数。

枚举这一列的高度\(h\)，设\(S(i, A, B, C, h)\)为这一列前\(i\)栋“楼房”，三种颜色分别使用\(A, B, C\)个，且最高一栋高度为\(h\)的方案数。

转移

对于\(F(N, A, B, C)\)，枚举第\(N\)列所使用的\(A', B', C'\)，答案加上\(F(N - 1, A - A', B - B', C - C') \times G(A', B', C')\)
对于\(G(A, B, C)\)，枚举这一列的最高高度\(h\)，答案加上\(S(N, A, B, C, h)\)
对于\(S(i, A, B, C, h)\)，分情况讨论：
- 第\(i\)栋楼房高度是\(h\)，枚举前\(i - 1\)栋楼房的最高高度\(h_2\)，并枚举\(A', B'\)，可以算出\(C' = h - A' - B'\)，
  
  答案加上\(S(i - 1, A - A', B - B', C - C', h_2) \times MultiP(A', B', C')\)。
- 高度为\(h\)的楼房在前\(i - 1\)栋中，枚举第\(i\)栋楼房的高度\(h_2\)，仍然枚举\(A', B'\)，算出\(C' = h - A' - B'\)，
  
  答案加上\(S(i - 1, A - A', B - B', C - C', h) \times MultiP(A' - (h - h_2), B', C')\)。
  
  这里注意楼房顶层的\((h - h_2)\)块立方体颜色已经确定了。所以计算多重排列时要将这一栋的\(A'\)减去\((h - h_2)\)

转成公式，就是：

1：
\[ \large F(N, A, B, C) = \displaystyle \sum _ {A', B', C'} F(N - 1, A - A', B - B', C - C') \times G(A', B', C') \\ \]
2：
\[ \large G(A, B, C) = \displaystyle \sum _ {h \le A} S(N, A, B, C, h) \\ \]
3：
\[ \large S(i, A, B, C, h) \\ =\displaystyle \sum _ {A' + B' + C' = h_2 \le h} S(i - 1, A - A', B - B', C - C', h) \times MultiP(A', B', C') \\ +\displaystyle \sum _ {h_2 \le A' + B' + C' = h} S(i - 1, A - A', B - B', C - C', h_2) \times MultiP(A' - (h - h_2), B', C') \]
时间复杂度：\(O(N^8)\)

优化 1

我们发现只有颜色\(A\)对答案才有关键影响，因此我们可以将颜色\(B, C\)合并，统一当成同一种颜色\(BC\)。

在最后计算答案时将\(F\)函数乘上\(C(BC, B)\)，从而将\(B\)和\(C\)从\(BC\)中分离出来。

实现上，可以直接将\(B+C\)代入\(O(N^8)\)算法的\(B\)中，将\(C\)置为\(0\)。
\[ 答案 = F(N, A, B +C, 0) \times C(B +C, B) \]

优化2

运用优化1的思想，我们发现\(F\)和\(G\)中的\(A\)已必不可少。但仔细思考发现所有蓝色立方体中，只有\(h\)个可以对答案产生关键影响。因此我们可以在\(G\)中运用组合数，将\(S\)中的\(A\)一维去掉。

优化后的DP方程

设\(F(N, A, BC)\)为在前\(N\)列中，使用\(A\)个蓝色立方体和共\(BC\)个红、绿色立方体摆成合法建筑物的方案数。

设\(G(A, BC)\)为在单独一列中，使用\(A\)个蓝色立方体和共\(BC\)个红、绿色立方体摆成合法建筑物的方案数。

设\(S(i, cnt, h)\)为在单独一列的前\(i\)栋楼房中，共使用\(cnt\)个立方体，摆成楼房最高刚好为\(h\)层的方案数。

转移方程：

1：
\[ \large F(N, A, BC) = \displaystyle \sum _ {A', BC'} F(N - 1, A - A', BC - BC') \times G(A', BC') \]
2：
\[ \large G(A, BC) = \displaystyle \sum _ {h \le A} S(N, A + BC, h) \times C(A + BC - h, A - h) \]
3：
\[ \large S(i, cnt, h) =\displaystyle \sum _ {h_2 \le h} S(i - 1, cnt - h_2, h) +\displaystyle \sum _ {h_2 < h} S(i - 1, cnt - h, h_2) \]
答案：
\[ \large 答案 = F(N, A, B + C) \times C(B + C, B) \]

注意事项

在方程2中，组合数是\(C(A + BC - h, A - h)\)而非\(C(A + BC, A)\)。

这是因为有刚好\(h\)个蓝色方块的是唯一确定的。

代码

为了调试加了很多条件编译，有点丑

#include <bits/stdc++.h>
// 0: Normal
// 1: Debugging
// 2: Debugging (test output)
// 3: Submit
#define __MODE__ 3
#if __MODE__ == 1 || __MODE__ == 2
int tab_cnt;
#define TAB { for (int i = 1; i <= tab_cnt; i++) printf("\t"); }
#define FUNC_IN(...) { TAB printf(__VA_ARGS__); tab_cnt++; }
#define FUNC_OUT(...) { TAB printf(__VA_ARGS__); tab_cnt--; }
#else
#define TAB
#define FUNC_IN(...)
#define FUNC_OUT(...)
#endif
using namespace std;
typedef long long LL;
const int kN = 25 + 5;
const int kMod = 1000000007;
// MultiP
const int kPriCnt = 10;
const int kPri[kPriCnt] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29};
int factor_cnt[kPriCnt];
void FactorDecom(int x, int sign) {
  for (int i = 0; i < kPriCnt; i++) {
    if (x % kPri[i] == 0) factor_cnt[i] += sign;
  }
}
LL arr_mp[kN][kN];
LL MultiP(int a, int b) {
  if (arr_mp[a][b] != -1) {
#if __MODE__ == 1 || __MODE__ == 2
    TAB printf("MultiP(%d, %d) = %lld\n", a, b, arr_mp[a][b]);
#endif
    return arr_mp[a][b];
  }
  int n = a + b;
  for (int i = 1; i <= n; i++) FactorDecom(i, 1);
  for (int i = 1; i <= a; i++) FactorDecom(i, -1);
  for (int i = 1; i <= b; i++) FactorDecom(i, -1);
  LL ans = 0;
  for (int i = 0; i < kPriCnt; i++) {
    while (factor_cnt[i]--) ans = ans * kPri[i] % kMod;
  }
#if __MODE__ == 1 || __MODE__ == 2
  TAB printf("MultiP(%d, %d) = %lld\n", a, b, ans);
#endif
  return arr_mp[a][b] = ans;
}
// Var
int n0, a0, b0, c0;
// Combination
LL arr_c[kN * 3][kN * 3];
LL C(int n, int m) {
  if (m == 0 || m == n) {
    return 1;
  } else if (arr_c[n][m] != -1) {
    return arr_c[n][m];
  } else {
    return arr_c[n][m] = (C(n - 1, m) + C(n - 1, m - 1)) % kMod;
  }
}
// DP
LL arr_s[kN][kN * 3][kN * 3];
LL S(int i, int cnt, int h) {
  FUNC_IN("S(%d, %d, %d)\n", i, cnt, h);
  if (cnt < h) {
    FUNC_OUT("S(%d, %d, %d) = %d (Judgement: cnt < h)\n", i, cnt, h,
             0);
    return 0;
  } else if (i == 1) {
    FUNC_OUT("S(%d, %d, %d) = %d (Judgement: i == 1)\n", i, cnt, h,
             cnt == h);
    return cnt == h;
  } else if (arr_s[i][cnt][h] != -1) {
    FUNC_OUT("S(%d, %d, %d) = %lld (Memory)\n", i, cnt, h,
             arr_s[i][cnt][h]);
    return arr_s[i][cnt][h];
  } else {
    LL ans = 0;
    // This = h
    for (int h2 = 0; h2 < h; h2++) {
      ans = (ans + S(i - 1, cnt - h, h2)) % kMod;
    }
    // This = h2
    for (int h2 = 0; h2 <= h; h2++) {
      ans = (ans + S(i - 1, cnt - h2, h)) % kMod;
    }
    FUNC_OUT("S(%d, %d, %d) = %lld (Calculation)\n", i, cnt, h,
             ans);
    return arr_s[i][cnt][h] = ans;
  }
}
LL arr_g[kN][kN * 2];
LL G(int a, int bc) {
  FUNC_IN("G(%d, %d)\n", a, bc);
  if (arr_g[a][bc] != -1) {
    FUNC_OUT("G(%d, %d) = %lld (Memory)\n", a, bc,
             arr_g[a][bc]);
    return arr_g[a][bc];
  } else {
    LL ans = 0;
    for (int h = 0; h <= a; h++) {
      ans = (ans + S(n0, a + bc, h) * C(a + bc - h, a - h) % kMod) % kMod;
    }
    FUNC_OUT("G(%d, %d) = %lld (Calculation)\n", a, bc,
             ans);
    return arr_g[a][bc] = ans;
  }
}
LL arr_f[kN][kN][kN * 2];
LL F(int n, int a, int bc) {
  FUNC_IN("F(%d, %d, %d)\n", n, a, bc);
  if (n == 1) {
    LL ans = G(a, bc);
    FUNC_OUT("F(%d, %d, %d) = %lld (Judgement)\n", n, a, bc,
             ans);
    return ans;
  } else if (arr_f[n][a][bc] != -1) {
    FUNC_OUT("F(%d, %d, %d) = %lld (Memory)\n", n, a, bc,
             arr_f[n][a][bc]);
    return arr_f[n][a][bc];
  } else {
    LL ans = 0;
    for (int a2 = 0; a2 <= a; a2++) {
      for (int bc2 = 0; bc2 <= bc; bc2++) {
        LL f = F(n - 1, a - a2, bc - bc2);
        LL g = G(a2, bc2);
        ans = (ans + f * g % kMod) % kMod;
      }
    }
    FUNC_OUT("F(%d, %d, %d) = %lld (Calculation)\n", n, a, bc,
             ans);
    return arr_f[n][a][bc] = ans;
  }
}
int T;
int main() {
#if __MODE__ == 0
  printf("longlongzhu123:\n");
#endif
#if __MODE__ == 3 || __MODE__ == 2
  freopen("2806.in", "r", stdin);
  freopen("2806.out", "w", stdout);
#endif
  memset(arr_c, -1, sizeof(arr_c));
  memset(arr_mp, -1, sizeof(arr_mp));
  scanf("%d", &T);
  while (T--) {
    memset(arr_s, -1, sizeof(arr_s));
    memset(arr_g, -1, sizeof(arr_g));
    memset(arr_f, -1, sizeof(arr_f));
    scanf("%d %d %d %d", &a0, &b0, &c0, &n0);
    LL ans = 0;
    ans = (ans + F(n0, a0, b0 + c0) * C(b0 + c0, c0) % kMod) % kMod;
    ans = (ans + F(n0, b0, a0 + c0) * C(a0 + c0, a0) % kMod) % kMod;
    ans = (ans + F(n0, c0, a0 + b0) * C(a0 + b0, a0) % kMod) % kMod;
    printf("%lld\n", ans);
  }
  return 0;
}