我 T M 需 要 练 一 下 D F S
\(\mathrm{T1}\)
其实用一张图就能说明白。
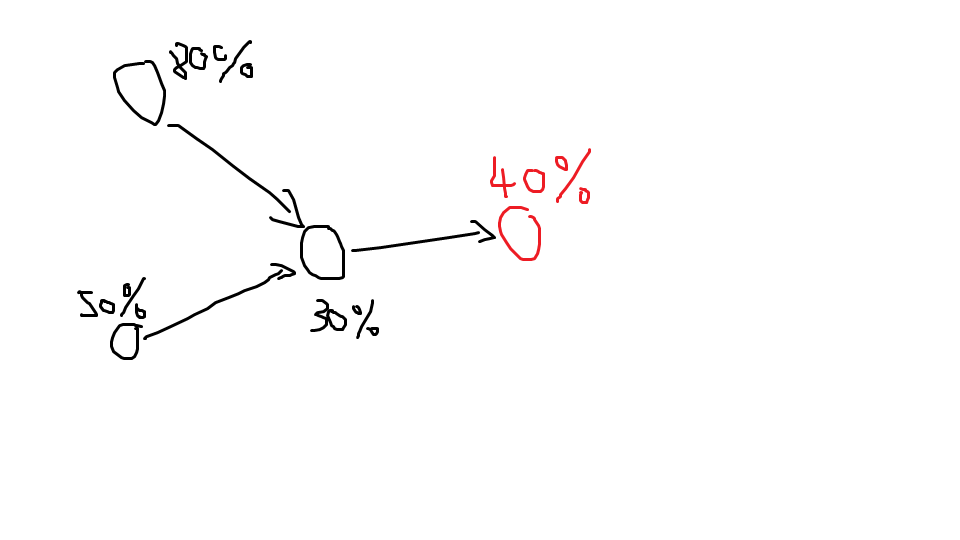
对于红点,它被找到的概率为
\[\mathrm{P=1-(1-80\%)(1-50\%)(1-30\%)(1-40\%)=4.2\%}\]
(利用容斥原理)
代码挺简单的,tmd就是DFS写错了。
\(\mathrm{T2}\)
首先可以发现,如果玩家能挺到最后,那他肯定把每一关能拿到的金币都拿到了,
所以答案至少有\(\sum\limits_{i=1}^{n}value_i\)。
然后因为死了之后金币会重置,所以当我们挺到最后时,我们只会在一个关卡捡到上次死了之后遗落的金币。
如果用\(f_i\)表示在第\(i\)关死亡后遗落金币数的期望值,用\(fp_i\)表示玩家恰好死在第\(i\)关的概率,那么答案就等于
\[\sum\limits_{i=1}^{n}(value_i+f_i\times fp_i)\]
接下来重点看\(f_i\)怎么求。

其实也很简单,你能挺到第\(i\)关的话,说明你肯定把前\(i-1\)关的金币都拿到了,而且在这前\(i\)关中你肯定只会捡到一次遗落在地上的金币,所以我们只要枚举一下你在哪一关捡到了金币即可。
为了方便,可以预处理出\(\sum\limits_{j=1}^{i}value_j\)的值,用\(sv_i\)表示
也就是说:
\[f_i=sv_{i-1}+\sum\limits_{j=1}^{i}f_j \times fp_j\]
为了避免转移到自己,我们把式子右边的\(f_{k=i}\)移到左边,得到
\[f_i=\dfrac{sv_{i-1}+\sum\limits_{j=1}^{i-1}f_j \times fp_j}{1-fp_i}\]
然后就可以了。
\(\mathrm{T3}\)
首先可以发现\(m\)最大只有\(50\),所以我们可以把\(0\sim49\)这\(50\)个数字分开搞。
对于每个数字,设\(sum_i\)表示原数组的前\(i\)个元素中有多少个当前所求的数字。
根据数组有主元素的定义:一个区间\((l,r]\)有主元素当且仅当:
\[sum_r-sum_l>\frac{r-l}{2}\]
可以推导出:
\[2(sum_r-sum_l)>r-l\]
去括号、移项可得:
\[2sum_r-r>2sum_l-l\]
也就是说,对于每个\(sum_r\),只需要求出有多少个\(2sum_l-l\)满足上面的式子即可。
这种区间查询个数的问题不是可以用树状数组吗
但是因为\(2sum_i-i\)可能小于\(0\),所以在树状数组中修改时要加上大约\(10^5\)的偏移量。