注意力机制（二）——在计算机视觉中的应用

惯例，除了蓝字都不是我写的。

在计算机视觉里attention应用在目标检测、语义分割等方面。在之前的机器翻译里提到了CNN的特点，图像领域最常用的就是CNN方法。

Non-local Neural Networks

Local这个词主要是针对感受野(receptive field)来说的。以卷积操作为例，它的感受野大小就是卷积核大小，而我们一般都选用3*3，5*5之类的卷积核，它们只考虑局部区域，因此都是local的运算。全连接就是non-local的，而且是global的。但是全连接带来了大量的参数，给优化带来困难。

提出问题：CNN事实上只能获取局部信息，是通过层叠来增大感受野，在某一时刻只能处理一个局部区域。想要捕捉long-range dependencies(此处range可理解为time、distance)，就只能重复地执行上述操作，通过数据逐步传递信号。

这样会导致：1.计算量大 2.优化困难，需要小心处理 3.难以构建multihop dependency model(多跳依赖模型)。

解决方法：本文提出非局部模块来捕捉long-range依赖，计算所有位置上特征的的加权和来作为对应位置的响应。这组位置可以是空间、时间或者时空坐标上的，这也就意味着这种泛化的非局部操作可以应用于图片、序列和视频问题。

特点：

1、non-local操作不考虑时空距离，而是通过直接计算两个位置间的交互来捕捉long-range依赖这里模糊了欧式距离这种计算方法其实就是求自相关矩阵，只不过是泛化的自相关矩阵.

2、non-local操作高效，只需少量几层就能实现很好的效果（non-local neural networks比现有的2D和3D convolutional networks的视频分类精度高）

3、non-local操作维持变量输入原先的大小，因此能方便地与其他操作相结合（因为pixel-pixel计算开销比较大，所以使用在 Mask R-CNN的基础上应用non-local block）

理念：

只在高阶语义层中引入non-local layer或者通过对embedding( $\theta, \phi$ )的结果加pooling层来减少计算量

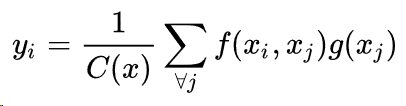
x为输入信号，可以是图片、序列或者视频，通常是它们的特征；x_i是一个向量，维数跟x的channel数一样 self-attention
y为输出信号，与x相同尺寸；
i和j是位置的索引，它可以是空间、时间或者时空上的位置
g是一个映射函数，将一个点映射成一个向量，可以看成是计算一个点的特征。
f(a,b)函数用于计算a与b之间关系的相关
C(x)为正规化因子

以图像为例，为了简化问题，作者简单地设置g函数为一个1*1的卷积，其实就是对原图做了一个线性变换。相似性度量函数f的选择有多种。

Gaussian: $f(\mathbb{x}_i, \mathbb{x}_j)=e^{\mathbb{x}_i^T \cdot \mathbb{x}_j}, \mathcal{C}(x)=\sum_{\forall j} f(\mathbb{x}_i, \mathbb{x}_j)$
Embedded Gaussian: $f(\mathbb{x}_i, \mathbb{x}_j)=e^{\theta(\mathbb{x}_i)^T \cdot \phi(\mathbb{x}_j)}, \mathcal{C}(x)=\sum_{\forall j} f(\mathbb{x}_i, \mathbb{x}_j)$
Dot Product: $f(\mathbb{x}_i, \mathbb{x}_j)=\theta(\mathbb{x}_i)^T \cdot \phi(\mathbb{x}_j), \mathcal{C}(x)=|\{i|i \text{ is a valid index of } \mathbb{x}\}|$
Concatenation: $f(\mathbb{x}_i, \mathbb{x}_j)=\text{ReLU}(\mathbb{w}_f^T \cdot [\theta(\mathbb{x}_i), \phi(\mathbb{x}_j)]), \mathcal{C}(x)=|\{i|i \text{ is a valid index of } \mathbb{x}\}|$ ，这相当于embedded的两个点拼接作为带ReLU激活函数全连接层的输入。它在visual reasoning中用的比较多。

为了能让non-local操作作为一个组件，可以直接插入任意的神经网络中，作者把non-local设计成residual block的形式，让non-local操作去学x的residual：

Wz实际上是一个卷积操作，它的输出channel数跟x一致。这样以来，non-local操作就可以作为一个组件，组装到任意卷积神经网络中

具体实现

原文考虑的是T帧的视频为例，这里以一个batch的图像、f选为embedded Gaussian为例，对于其他形式的相似性度量，可以类似地化为矩阵操作。

如果在尺寸很大的输入上应用non-local layer，也是计算量很大的。后者的解决方案是，只在高阶语义层中引入non-local layer。还可以通过对embedding( $\theta, \phi$ )的结果加pooling层来进一步地减少计算量。

对于前者，注意到f的计算可以化为矩阵运算，我们实际上可以将整个non-local化为矩阵乘法运算+卷积运算。如下图所示，其中oc为output_channels，卷积操作的输出filter数量。

比较：

1、跟全连接层的联系

我们知道，non-local block利用两个点的相似性对每个位置的特征做加权，而全连接层则是利用position-related的weight对每个位置做加权。于是，全连接层可以看成non-local block的一个特例：

任意两点的相似性仅跟两点的位置有关，而与两点的具体坐标无关，即 $f(\mathbb{x}_i, \mathbb{x}_j)=w_{ij}$
g是identity函数， $g(\mathbb{x}_i)=\mathbb{x}_i$
归一化系数为1。归一化系数跟输入无关，全连接层不能处理任意尺寸的输入。

2、跟机器翻译的Self-attention的联系
non-local block主要是一个non-local均值计算，具体的算法方法如下公式（1）：

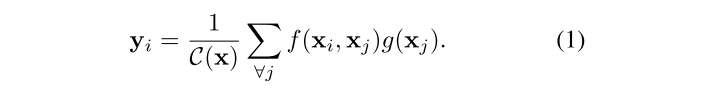
同样，下面给出了机器翻译中的Self Attention的具体计算公式：

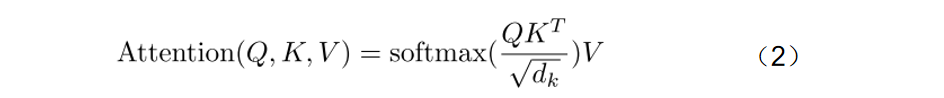
通过对比公式(2)和公式(1)可以发现，当公式(1)中的f函数具体化为softmax，C(x)操作赋值为Xj维度的开根号时，两个公式是等价的。此时可以看出，f函数中的Xi变量等价于公式(2)中的Q，Xj等价于K，g函数中的Xj等价于变量V。

本文里Embedded Gaussian: $f(\mathbb{x}_i, \mathbb{x}_j)=e^{\theta(\mathbb{x}_i)^T \cdot \phi(\mathbb{x}_j)}, \mathcal{C}(x)=\sum_{\forall j} f(\mathbb{x}_i, \mathbb{x}_j)$

Embedding的1*1卷积操作可以看成矩阵乘法：

$\theta(\mathbb{x}_i)= W_{\theta} \cdot \mathbb{x}_i; \quad \phi(\mathbb{x}_j)=W_{\phi} \cdot \mathbb{x}_j \quad \Rightarrow \quad \theta(\mathbb{x})= W_{\theta} \cdot \mathbb{x}; \quad \phi(\mathbb{x})= W_{\phi} \cdot \mathbb{x}$

于是，

$y=\text{softmax}(\mathbb{x}^T \cdot W_{\theta}^T \cdot W_\phi \cdot \mathbb{x}) \cdot g(\mathbb{x})$

图像的embedding层

我们把一个12个元素的矩阵变成6个元素的矩阵，直观上大小缩小了一半

embedding层，在某种程度上，就是用来降维的，降维的原理就是矩阵乘法。在卷积网络中，可以理解为特殊全连接层操作，跟1x1卷积核异曲同工

假如我们有一个100W X10W的矩阵，用它乘上一个10W X 20的矩阵，我们可以把它降到100W X 20，这就是嵌入层的一个作用——降维。然后中间那个10W X 20的矩阵，可以理解为查询表，也可以理解为映射表，也可以理解为过度表

embedding可以降维，当然可以升维。对低维的数据进行升维时，可能把一些其他特征放大了，或者把笼统的特征分开了。

---------------------
作者：罗大黑
来源：CSDN
原文：https://blog.csdn.net/weixin_42078618/article/details/82999906

原文来源

non-local 笔记 https://zhuanlan.zhihu.com/p/52510471 https://zhuanlan.zhihu.com/p/33345791 https://zhuanlan.zhihu.com/p/53155423

注意力机制（二）——在计算机视觉中的应用

Non-local Neural Networks

猜你喜欢