概率论在机器学习中有很重要的地位,本篇总结一下我对贝叶斯公式和全概率公式的理解。
1、全概率公式的定义
因为公式本身就比较抽象,一开始就列举公式很不友好,因此先举个栗子抛砖引玉:
【问题1】现追捕某犯罪嫌疑人,据分析他外逃、市内藏匿和自首的概率依次为0.3,0.5,0.2。并且在外逃以及市内藏匿成功缉拿的概率依次是0.4,0.7。问该犯罪嫌疑人最终归案的概率是多少?
【解答】设该犯罪嫌疑人最终归案为事件A,外逃、市内藏匿和自首分别为事件B1,B2,B3。则在外逃的情况下被成功缉拿的概率为
,在市内藏匿被成功缉拿的概率为
,自首则肯定被成功缉拿概率为
,最终被成功缉拿归案的概率为以上三者相加:
。
在这个例子里,包含了这个逃犯所有的选择情况,且各个选择之间互不相关,即
。
从上面的问题1可以总结出全概率公式的定义:
设B1,B2,...为有限或者无限个事件,它们两两互斥且在每次实验中至少发生一个,即满足:,且
,A为任一事件(下图中红圈内部)。形象的如下图表示:
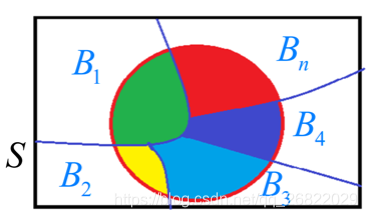
则事件A发生的概率为:
上面的公式就叫做全概率公式。
2、全概率公式的意义
全概率公式的意义在于,当直接计算P(A)较为困难,而P(Bi), P(A|Bi) (i=1,2,...)的计算较为简单的时候,可以使用全概率公式计算P(A)。思想就是将事件A分解成若干小时间,通过求每个小事件的概率相加后求得事件A的概率。
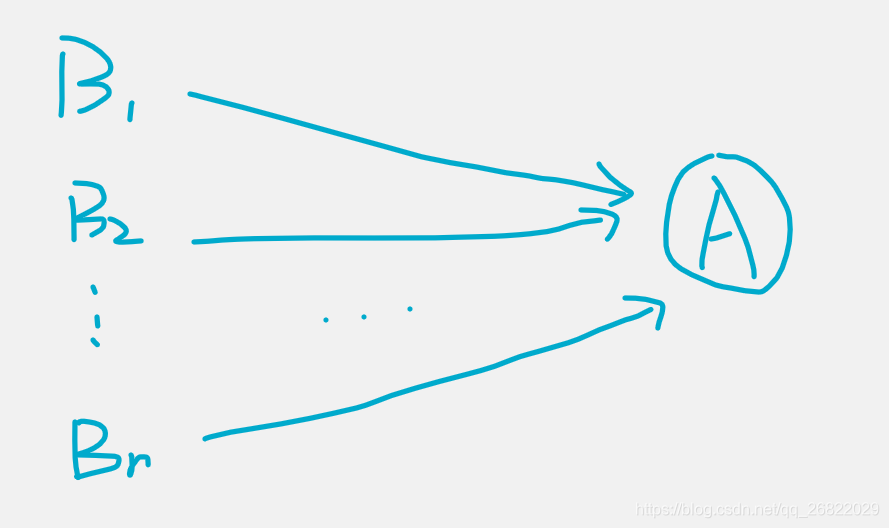
我们可以将事件A看作问题的结果,将事件Bi看作问题的原因i。那么全概率公式是将可能引起事件A发生的所有可能原因{B1, B2, ... Bn}均看作单一的事件,通过将这个问题拆分,分别求出不同的起因情况下事件发生的概率之后,再汇总起来的。仍是是由原因到结果的一种解法。
3、贝叶斯公式的定义
【问题2】接着问题1,加入现在已知该逃犯被抓捕,求他是因为自首被抓捕归案的概率是多少?
【解答】在问题1中已经知道,嫌疑人最终可以因为三种情况被抓捕归案,分别是外逃、市内藏匿和投案自首。现在已经知道他被抓捕了,那么肯定是这三种情况之中的一种,现在题目求的是因为自首被抓捕归案的概率(在“因为自首而被抓捕归”案这个事件中,被抓捕归案是条件)这个事件的概率为:
与全概率公式解决的问题相反,贝叶斯公式是建立在条件概率的基础上寻找事情发生的原因,设B1,B2,...是样本空间S的一个划分,则对任意事件A(P(A)>0)有:
上面的公式即为贝叶斯公式,Bi常被认为是导致A放生的原因,因此P(Bi)(i=1,2,...)表示各种原因发生的可能性大小,因此称之为先验概率(权重);而P(Bi|A)(i=1,2,...)则反映了当产生了结果A之后,再对各种原因概率的新认识,称为后验概率。

4、贝叶斯公式的理解
贝叶斯公式恰好和全概率公式相反,作用在于“由结果推原因”:现在结果A已经发生了,再众多的原因中,某个原因导致事件发生的概率是多少呢?这个过程是反过来的。