三角剖分是一种应用非常广泛的面重建技术。三角剖分将一些散乱的点云数据剖分为一些系列的三角网格。最常见的三角剖分技术是Delaunay三角剖分。Delaunay三角剖分具有许多优良的性质。如最大化最小角特性，即在所有可能的三角剖分中，其所生成的三角形的最小角的角度最大。所以，Delaunay三角剖分无论从那个区域开始构建，最终生成的三角网格是唯一的。

基本概念

问题描述

如何把一个散点集合剖分成不均匀的三角形网格，这就是散点集的三角剖分问题，散点集的三角剖分，对数值分析以及图形学来说，都是极为重要的一项预处理技术。该问题图示如下：
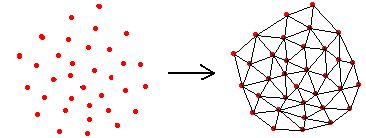
在这里插入图片描述

三角剖分定义

三角剖分：假设V是二维实数域上的有限点集，边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G，该平面图满足条件：

除了端点，平面图中的边不包含点集中的任何点。
没有相交边。
平面图中所有的面都是三角面，且所有三角面的合集是散点集V的凸包。

Delaunay三角剖分的定义

在实际中运用的最多的三角剖分是Delaunay三角剖分，它是一种特殊的三角剖分。先从Delaunay边说起。Delaunay边的定义：假设E中的一条边e（两个端点为a,b），e若满足下列条件，则称之为Delaunay边：存在一个圆经过a,b两点，圆内(注意是圆内，圆上最多三点共圆)不含点集V中任何其他的点，这一特性又称空圆特性。Delaunay三角剖分的定义：如果点集V的一个三角剖分T只包含Delaunay边，那么该三角剖分称为Delaunay三角剖分。

Delaunay三角剖分的准则

      要满足Delaunay三角剖分的定义，必须符合两个重要的准则：
      1、空圆特性：Delaunay三角网是唯一的（任意四点不能共圆），在Delaunay三角形网中任一三角形的外接圆范围内不会有其它点存在。如下图所示：
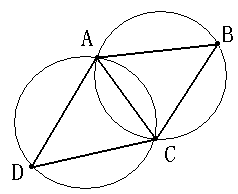
在这里插入图片描述
      2、最大化最小角特性：在散点集可能形成的三角剖分中，Delaunay三角剖分所形成的三角形的最小角最大。从这个意义上讲，Delaunay三角网是“最接近于规则化的“的三角网。具体的说是指在两个相邻的三角形构成凸四边形的对角线，在相互交换后，六个内角的最小角不再增大。如下图所示：
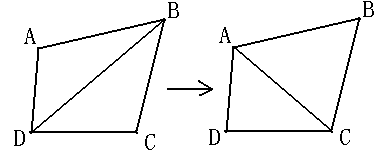
在这里插入图片描述

局部最优化处理

理论上为了构造Delaunay三角网，Lawson提出的局部优化过程LOP(Local Optimization Procedure)，一般三角网经过LOP处理，即可确保成为Delaunay三角网，其基本做法如下所示：
1.将两个具有共同边的三角形合成一个多边形。
2.以最大空圆准则作检查，看其第四个顶点是否在三角形的外接圆之内。
3.如果在，修正对角线即将对角线对调，即完成局部优化过程的处理。
LOP处理过程如下图所示：
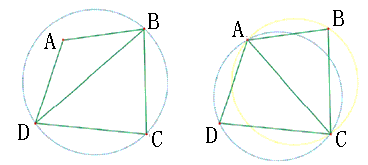
在这里插入图片描述

Delaunay剖分的算法

Delaunay剖分是一种三角剖分的标准，实现它有多种算法。Delaunay三角形的算法，有翻边算法、逐点插入算法、分割合并算法、Bowyer-Watson算法等。
在这里插入图片描述
由上图可以看出，三角网生成法的时间效率最低，分治算法的时间效率最高，逐点插入法效率居中。由于区域生长法本质的缺陷，导致其效率受限，这种方法在80年代中期以后已经很少使用。分治算法时间效率相对较高，但是由于其递归执行，所以需要较大的内存空间，导致其空间效率较低。此外，分治法的数据处理及结果的优化需要的工作量也比较大。逐点插入算法实现简单，时间效率比较高，而运行占用的空间也较小，从时间效率和空间效率综合考虑，性价比最高，因而应用广泛。1977年，Lawson提出了逐点插入法建立Delaunay三角网的算法思想。之后Lee和Schachlter,Bowyer,Watson,Sloan,先后进行了发展和完善。他们的算法在初始化三角网的建立方法、定位点所在三角形的过程、以及插入的过程方面各具特点。

Lawson算法

逐点插入的Lawson算法是Lawson在1977年提出的，该算法思路简单，易于编程实现。基本原理为：首先建立一个大的三角形或多边形，把所有数据点包围起来，向其中插入一点，该点与包含它的三角形三个顶点相连，形成三个新的三角形，然后逐个对它们进行空外接圆检测，同时用Lawson设计的局部优化过程LOP进行优化，即通过交换对角线的方法来保证所形成的三角网为Delaunay三角网。
上述基于散点的构网算法理论严密、唯一性好，网格满足空圆特性，较为理想。由其逐点插入的构网过程可知，遇到非Delaunay边时，通过删除调整，可以构造形成新的Delaunay边。在完成构网后，增加新点时，无需对所有的点进行重新构网，只需对新点的影响三角形范围进行局部联网，且局部联网的方法简单易行。同样，点的删除、移动也可快速动态地进行。但在实际应用当中，这种构网算法当点集较大时构网速度也较慢，如果点集范围是非凸区域或者存在内环，则会产生非法三角形。

Bowyer-Watson算法

目前采用逐点插入方式生成的Delaunay三角网的算法主要基于Bowyer-Watson算法，Bowyer-Watson算法的主要步骤如下：

建立初始三角网格：针对给定的点集V,找到一个包含该点集的矩形R,我们称R为辅助窗口。连接R的任意一条对角线，形成两个三角形，作为初始Delaunay三角网格。
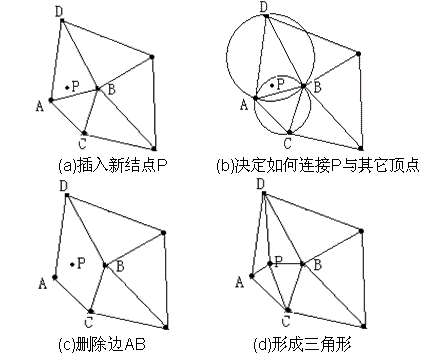
逐点插入：假设目前已经有一个Delaunay三角网格T,现在在它里面再插入一个点P,需要找到该点P所在的三角形。从P所在的三角形开始，搜索该三角形的邻近三角形，并进行空外接圆检测。找到外接圆包含点P的所有的三角形并删除这些三角形，形成一个包含P的多边形空腔，我们称之为Delaunay空腔。然后连接P与Delaunay腔的每一个顶点，形成新的Delaunay三角网格。
删除辅助窗口R:重复步骤2）,当点集V中所有点都已经插入到三角形网格中后，将顶点包含辅助窗口R的三角形全部删除。
在这些步骤中，快速定位点所在的三角形、确定点的影响并构建Delaunay腔的过程是每插入一个点都会进行的。随着点数的增加，三角形数目增加很快，因此缩短这两个过程的计算时间，是提高算法效率的关键。算法执行图示如下：

示例演示

下面我们对优化过的Bowyer-Watson算法进行实现，伪代码如下：

input: 顶点列表(vertices)　　　　　　　　　　　　　　　　　　　　  　//vertices为外部生成的随机或乱序顶点列表
output:已确定的三角形列表(triangles)
　　　　初始化顶点列表
　　　　创建索引列表(indices = new Array(vertices.length))　　　　//indices数组中的值为0,1,2,3,......,vertices.length-1
　　　　基于vertices中的顶点x坐标对indices进行sort　　  　　　　　  //sort后的indices值顺序为顶点坐标x从小到大排序（也可对y坐标，本例中针对x坐标）
　　　　确定超级三角形
　　　　将超级三角形保存至未确定三角形列表（temp triangles）
　　　　将超级三角形push到triangles列表
　　　　遍历基于indices顺序的vertices中每一个点　　　　　　　　　  　//基于indices后，则顶点则是由x从小到大出现
　　　　　　初始化边缓存数组（edge buffer）
　　　　　　遍历temp triangles中的每一个三角形
　　　　　　　　计算该三角形的圆心和半径
　　　　　　　　如果该点在外接圆的右侧
　　　　　　　　　　则该三角形为Delaunay三角形，保存到triangles
　　　　　　　　　　并在temp里去除掉
　　　　　　　　　　跳过
　　　　　　　　如果该点在外接圆外（即也不是外接圆右侧）
　　　　　　　　　　则该三角形为不确定        　　　　　　　　　     //后面会在问题中讨论
　　　　　　　　　　跳过
　　　　　　　　如果该点在外接圆内
　　　　　　　　　　则该三角形不为Delaunay三角形
　　　　　　　　　　将三边保存至edge buffer
　　　　　　　　　　在temp中去除掉该三角形
　　　　　　对edge buffer进行去重
　　　　　　将edge buffer中的边与当前的点进行组合成若干三角形并保存至temp triangles中
　　　　将triangles与temp triangles进行合并
　　　　除去与超级三角形有关的三角形
end

C++代码下载。运行结果如下，与VTK图形处理之Delaunay三角剖分结果一样。
在这里插入图片描述

参考资料

Triangulate
三角剖分算法(delaunay)
VTK图形处理之Delaunay三角剖分

Delaunay三角剖分