（图论）树的直径

定义

树的直径有许多相近的定义。但由于没有找到比较权威的定义，就用自己的语言大概表述一下吧。
对于一棵带非负边权的树，定义两点间距离为两点间路径的边权之和，树的直径就是距离最远的两点之间的路径，同时也称该距离为树的直径。
简而言之，树的直径就是树上最长的简单路径。

性质

1. 直径两端点一定是两个叶子节点。

2. 距离任意点最远的点一定是直径的一个端点。

3. 对于两棵树，如果第一棵树直径两端点为(u,v)，第二棵树直径两端点为(x,y)，用一条边将两棵树连接，那么新树的直径一定是u,v,x,y中的两个点。

4. 若一棵树存在多条直径，那么这些直径交于一点且交点是这些直径的中点。

性质证明

1. 显然成立，证明从略。

2. 情况一：点a在直径\((u,v)\)上。若存在点b使得$ dis(a,b) \gt dis (a,u) \text{并且} dis(a,b) \gt dis (a,v)$ ，则有 \(dis(b,v) \text{或} dis(b,u) \gt dis(u,v)\)，即\((u,v)\)不是该树的直径，矛盾。
   情况二：点a不在直径\((u,v)\)上。若存在点b使得$ dis(a,b) \gt dis (a,u) \text{并且} dis(a,b) \gt dis (a,v)$ ，不妨取直径的其中一个端点\(u\)分析。
   分析图如下（灵魂画手上线）：
   

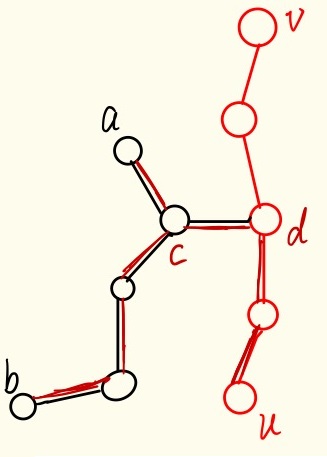
   图片注：u,v 为直径端点，c为\((a,b)\text{与}(a,u)\)交点，d为\((a,u)\text{与}(v,u)\)交点。

   由于\(dis(a,b) \gt dis (a,u)\) ,可知 \(dis(c,b) \gt dis (c,u)\)，进而得到\(dis(d,b) \gt dis (d,u)\)，最终可知\(dis(v,b) \gt dis (v,u)\)，，即\((u,v)\)不是该树的直径，矛盾。