DFS AND BFS
DFS的定义:
深度优先搜索在搜索过程中访问某个顶点后,需要递归地访问此顶点的所有未访问过的相邻顶点。 初始条件下所有节点为白色,选择一个作为起始顶点,按照如下步骤遍历: a. 选择起始顶点涂成灰色,表示还未访问 b. 从该顶点的邻接顶点中选择一个,继续这个过程(即再寻找邻接结点的邻接结点),一直深入下去,直到一个顶点没有邻接结点了,涂黑它,表示访问过了 c. 回溯到这个涂黑顶点的上一层顶点,再找这个上一层顶点的其余邻接结点,继续如上操作,如果所有邻接结点往下都访问过了,就把自己涂黑,再回溯到更上一层。 d. 上一层继续做如上操作,知道所有顶点都访问过。 用图可以更清楚的表达这个过程:
例:下图是一个无向图,如果我们从A点发起深度优先搜索(以下的访问次序并不是唯一的,第二个点既可以是B也可以是C,D),则我们可能得到如下的一个访问过程:A->B->E(没有路了!)则回溯到B,B没有其他邻接点,再回溯到A->C->F->H->G->D(没有路,最终又回溯到A,A也没有未访问的相邻节点,本次搜索结束).

DFS特点:
(1)深度优先搜索法有递归以及非递归两种设计方法。一般的,当搜索深度较小、问题递归方式比较明显时,用递归方法设计好,它可以使得程序结构更简捷易懂。当数据量较大时,由于系统堆栈容量的限制,递归容易产生溢出,用非递归方法设计比较好。
(2)不一定会得到最优解,这个时候需要修改原算法:把原输出过程的地方改为记录过程,即记录达到当前目标的路径和相应的路程值,并与前面已记录的值进行比较,保留其中最优的,等全部搜索完成后,才把保留的最优解输出。
递归代码实现:
#include <iostream> 2 #define N 5 3 using namespace std; 4 int maze[N][N] = { 5 { 0, 1, 1, 0, 0 }, 6 { 0, 0, 1, 0, 1 }, 7 { 0, 0, 1, 0, 0 }, 8 { 1, 1, 0, 0, 1 }, 9 { 0, 0, 1, 0, 0 } 10 }; 11 int visited[N + 1] = { 0, }; 12 void DFS(int start) 13 { 14 visited[start] = 1; 15 for (int i = 1; i <= N; i++) 16 { 17 if (!visited[i] && maze[start - 1][i - 1] == 1) 18 DFS(i); 19 } 20 cout << start << " "; 21 }
非递归代码实现:
#include <iostream> 2 #include <stack>//借助一个栈; 3 #define N 5 4 using namespace std; 5 int maze[N][N] = { 6 { 0, 1, 1, 0, 0 }, 7 { 0, 0, 1, 0, 1 }, 8 { 0, 0, 1, 0, 0 }, 9 { 1, 1, 0, 0, 1 }, 10 { 0, 0, 1, 0, 0 } 11 }; 12 int visited[N + 1] = { 0, }; 13 void DFS(int start) 14 { 15 stack<int> s; 16 s.push(start); 17 visited[start] = 1; 18 bool is_push = false; 19 while (!s.empty()) 20 { 21 is_push = false; 22 int v = s.top(); 23 for (int i = 1; i <= N; i++) 24 { 25 if (maze[v - 1][i - 1] == 1 && !visited[i]) 26 { 27 visited[i] = 1; 28 s.push(i); 29 is_push = true; 30 break; 31 } 32 } 33 if (!is_push) 34 { 35 cout << v << " "; 36 s.pop(); 37 } 38 39 } 40 }
例题1:(感觉像图像识别基础)
图像0的定义:存在1字符且1字符只能是由一个连通块组成,存在且仅存在一个由0字符组成的连通块完全被1所包围。
图像1的定义:存在1字符且1字符只能是由一个连通块组成,不存在任何0字符组成的连通块被1所完全包围。
连通的含义是,只要连续两个方块有公共边,就看做是连通。
完全包围的意思是,该连通块不与边界相接触。
每组测试数据包含:
第一行两个整数n,m表示图像的长与宽。
接下来n行m列将会是只有01组成的字符画。
满足1<=n,m<=100
Output如果这个图是1的话,输出1;如果是0的话,输出0,都不是输出-1。
Sample Input
32 32 00000000000000000000000000000000 00000000000111111110000000000000 00000000001111111111100000000000 00000000001111111111110000000000 00000000011111111111111000000000 00000000011111100011111000000000 00000000111110000001111000000000 00000000111110000001111100000000 00000000111110000000111110000000 00000001111110000000111110000000 00000001111110000000011111000000 00000001111110000000001111000000 00000001111110000000001111100000 00000001111100000000001111000000 00000001111000000000001111000000 00000001111000000000001111000000 00000001111000000000000111000000 00000000111100000000000111000000 00000000111100000000000111000000 00000000111100000000000111000000 00000001111000000000011110000000 00000001111000000000011110000000 00000000111000000000011110000000 00000000111110000011111110000000 00000000111110001111111100000000 00000000111111111111111000000000 00000000011111111111111000000000 00000000111111111111100000000000 00000000011111111111000000000000 00000000001111111000000000000000 00000000001111100000000000000000 00000000000000000000000000000000 32 32 00000000000000000000000000000000 00000000000000001111110000000000 00000000000000001111111000000000 00000000000000011111111000000000 00000000000000111111111000000000 00000000000000011111111000000000 00000000000000011111111000000000 00000000000000111111110000000000 00000000000000111111100000000000 00000000000001111111100000000000 00000000000001111111110000000000 00000000000001111111110000000000 00000000000001111111100000000000 00000000000011111110000000000000 00000000011111111110000000000000 00000001111111111111000000000000 00000011111111111111000000000000 00000011111111111111000000000000 00000011111111111110000000000000 00000000001111111111000000000000 00000000000000111111000000000000 00000000000001111111000000000000 00000000000111111110000000000000 00000000000011111111000000000000 00000000000011111111000000000000 00000000000011111111100000000000 00000000000011111111100000000000 00000000000000111111110000000000 00000000000000001111111111000000 00000000000000001111111111000000 00000000000000000111111111000000 00000000000000000000000000000000 3 3 101 101 011Sample Output
0 1 -1要点:
1:1连通块只能有一个,即所有1连在一起;
2:0在1连通块内部的连通块只有一个时表示0;
3:1连通块内部不存在0连通块时表示1;
4:1字符必须有,0字符可以没有;
代码实现:
char graph[104][104];
int visit[102][102];
int dir[2][4]={-1,1,0,0,0,0,-1,1}
int sign1(int i, int j) {//sign1用来记录1连通块的数量,超过1就失败
if (graph[i][j] == '1'&&visit[i][j]==0) {
visit[i][j] = 1;
sign1(i - 1, j);
sign1(i, j - 1);
sign1(i + 1, j);
sign1(i, j + 1);
return 1;
}
else return 0;
}
int p = 0;
int sign2(int i, int j) {//用来记录0连通块的数量;
if (graph[i][j] == '0'&&visit[i][j]==0) {
visit[i][j] = 1;
for(int k=0;k<4;++i)
sign2(i+dir[0][k],j+dir[1][k];
return 1;
}
else if (graph[i][j] == '*')//若递归过程中遇到'*',说明该0连通块接触了边界,不在一连通块的内部;
p = 1;
return 0;
}
例题2:
在实际运行中DFS可能会超时,这时需要用到剪枝。
第1行为两个整数m, n (1 ≤ m, n ≤ 100),分别表示迷宫的行数和列数,接下来m行,每行包括n个字符,其中字符'.'表示该位置为空地,字符'*'表示该位置为障碍,输入数据中只有这两种字符,每组测试数据的最后一行为5个整数k, x 1 , y 1 , x 2 , y 2 (1 ≤ k ≤ 10, 1 ≤ x 1 , x 2 ≤ n, 1 ≤ y 1 , y 2 ≤ m),其中k表示gloria最多能转的弯数,(x 1 , y 1 ), (x 2 , y 2 )表示两个位置,其中x 1 ,x 2 对应列,y 1 , y 2 对应行。
Output 每组测试数据对应为一行,若gloria能从一个位置走到另外一个位置,输出“yes”,否则输出“no”。Sample Input
2 5 5 ...** *.**. ..... ..... *.... 1 1 1 1 3 5 5 ...** *.**. ..... ..... *.... 2 1 1 1 3
代码实现:
#include<iostream>
using namespace std;
const int maxn = 110;
char graph[maxn][maxn];
bool visit[maxn][maxn];
int off_time[maxn][maxn];//记录上次到达graph[i][j]时的转弯次数;
int direction[4][2] = { -1,0,0,-1,1,0,0,1 };
int limit, tar_x, tar_y,row,col;
bool flag;
bool ok(int x, int y) {
if (graph[x][y] == '*' || visit[x][y])return false;
if (x <= 0 || x> row || y <= 0 || y> col)return false;
return true;
}
void dfs(int x, int y, int dir, int k) {
if (flag)return;//已经找到一条成功路径,不需要再找;
if (k > limit)return;
if (y ==tar_y&&x==tar_x) {
flag = true;
return;//直接结束此步
}
for (int i = 0; i < 4; i++) {
int ny = y+direction[i][1];
int nx = x+direction[i][0];
if (ok(nx, ny)) {
if (dir != i&&dir!=-1) {//-1表示在起点;
if (off_time[nx][ny] >=k+1) {//若k>off_time,不管之前从[nx][ny]进行下去有没有成功都不需要再进入了;
visit[nx][ny] = true;
off_time[nx][ny] = k+1;
dfs(nx, ny, i, k + 1);
visit[nx][ny] = false;//为下一次遍历做准备;
}
}
else {
if (off_time[nx][ny] >= k) {
visit[nx][ny] = true;
off_time[nx][ny] = k;
dfs(nx, ny, i, k);
visit[nx][ny] = false;
}
}
}
}
} 例题3:
八皇后问题
八皇后问题是一个以国际象棋为背景的问题:如何能够在 8×8 的国际象棋棋盘上放置八个皇后,使得任何一个皇后都无法直接吃掉其他的皇后,为了达到此目的,任两个皇后都不能处于同一条横行、纵行或斜线上。
思路:没放置一个皇后,就将其能够攻击的区域进行标记,然后放置下一个皇后,依次类推……;此外,如果有解最终肯定是每一行有且只有一位皇后,所以放置的时候按照逐行放置的顺序进行。此问题难点在于如何把控递归函数的返回条件,一种条件是8个皇后放置完成后,返回成功,一种条件是该行中已经没有可以放置的位置,此时返回失败,需要重新放置。此时要额外注意,所谓的“重新放置”指的并不是将所有皇后清除重新来过,而是只返回上一层,将上一个导致本次放置失败的皇后进行清除,然后重新更新其位置,通过逐级放置、或逐级回溯可以达到遍历所有情况找到所有解。
#include<stdio.h>
int a[10][10];
int sum=0;
int judge(int r,int c)
{
for(int i=0;i<8;i++)
{
if(a[i][c])
return 0;
}
for(int i=r,j=c;i>=0&&j>=0;i--,j--)
{
if(a[i][j])
return 0;
}
for(int i=r,j=c;i>=0&&j<8;i--,j++)
{
if(a[i][j])
return 0;
}
return 1;
}
void queen(int r)
{
if(r==8)
{
sum++;
return;
}
for(int i=0;i<8;i++)
{
if(judge(r,i))
{
a[r][i]=1;
queen(r+1);
a[r][i]=0;
}
}
}
int main()
{
queen(0);
printf("%d\n",sum);
return 0;
}judge()判断函数:
我们传参传过来了你所要放置皇后的下标,即位置,首先一个for循环判断它所在的这一个是否有被标记过,如果有就返回0,
它所在的行就不用判断了,因为我们就是一行一行的放置的。每行只放置一个所以就不用判断了;
对角线分为正对角线和反对角线
要注意是否越界的问题,所以是i>=0&&j>=0,在反对角线上是i>=0&&j<8
只需要判断你所放皇后以上部分就行了,因为下面的都还没有放,是一定符合判断的。
BFS的定义:
宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
代码实现:借助一个栈装依次访问的结点即可。
例题:
例一:
《迷宫问题》
定义一个二维数组:
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
int Count = 0;
void bfs(int x, int y) {
queue<Path>p;
p.push({ x,y,0,-1 });
path[Count++] = p.front();
visit[x][y] = 1;
while (!p.empty())
{
Path temp = p.front();
p.pop();
int xi = temp.x, yi = temp.y;
for (int i = 0; i < 4; ++i)
{
xi += dir[0][i];
yi += dir[1][i];
if (judge(xi, yi) == 1) {
p.push({ xi,yi,Count,temp.sign });
path[Count++] = p.back();//坑死我了,写p.front(),调到死啊,在对尾入队哦;
visit[xi][yi] = 1;
}
if (xi == 0 && yi == 0)return;
}
}
}例2:
一个有意思的题;
题意:农夫知道一头牛的位置,想要抓住它。农夫和牛都位于数轴上,农夫起始位于点N(0<=N<=100000),牛位于点K(0<=K<=100000)。
农夫有两种移动方式:
1、从X移动到X-1或X+1,每次移动花费一分钟
2、从X移动到2*X,每次移动花费一分钟
假设牛没有意识到农夫的行动,站在原地不动。农夫最少要花多少时间才能抓住牛?
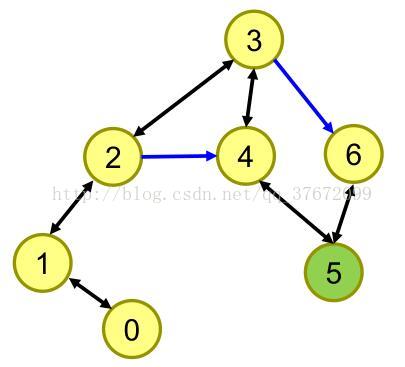
假设农夫起始位于点3,牛位于5,N=3,K=5,最右边是6。
如何搜索到一条走到5的路径?
这题将线性问题转换成了图的最短路问题,用BFS即可得;
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
int n,k;
const int MAXN=100010;
int visited[MAXN];//判重标记,visited[i]=true表示i已经拓展过
struct step
{
int x;//位置
int steps;//到达x所需的步数
step(int xx,int s):x(xx),steps(s) {}
};
queue<step>q;//队列
int main()
{
cin>>n>>k;
memset(visited,0,sizeof(visited));
q.push(step(n,0));
visited[n]=1;
while(!q.empty())
{
step s=q.front();
if(s.x==k)//找到目标
{
cout<<s.steps<<endl;
return 0;
}
else
{
if(s.x-1>=0 && !visited[s.x-1])
{
q.push(step(s.x-1,s.steps+1));
visited[s.x-1]=1;
}
if(s.x+1<=MAXN && !visited[s.x+1])
{
q.push(step(s.x+1,s.steps+1));
visited[s.x+1]=1;
}
if(s.x*2<=MAXN&&!visited[s.x*2])
{
q.push(step(s.x*2,s.steps+1));
visited[s.x*2]=1;
}
q.pop();
}
}
return 0;
} 例3:pots:
有两个不同的瓶子,初始时为空, 可以进行3种操作:
1:fill 加满水
2:drop 把水倒空
3:pour 把一个瓶中的水倒入另一个瓶子,如果另一个瓶子被装满则停止倒入
输入两个瓶子的容量和当任意瓶子中水到达多少时就停止的这个值,输出最短操作步骤
转换成图的搜索问题:
设(i,j)为瓶1与瓶2在某一时刻的容量,那么从这点出发,可以到达的点有:
(A, j) : FILL(1)
(i, B) : FILL(2)
(0, j): DROP(1)
(i, 0): DROP(2)
(i+j, 0) or (A, j-A+i) : POUR(2,1)//若A没被加满,则B一定变为了0,若A被加满了,B不一定为0;
(0, i+j) or (i-B+j, B) : POUR(1,2)
则每次搜索时有6个方向,对于i和j都是有范围的,超过范围则return,当i,或j的值变成所求值时就成功;由于求最短步骤故BFS;
代码实现:
#include <iostream>
#include <queue>
using namespace std;
int *color;
int *pi;
int *d;
int *operation; //保存操作
int BFS(int A,int B,int C)
{
if(C==0)
return 0;
int num[2]={A,B};
int temp=(A+1)*(B+1);
color=new int[temp];
pi=new int[temp];
d=new int[temp];
operation=new int[temp];
for(int i=0;i<temp;i++)
{
color[i]=0;
pi[i]=0;
d[i]=0;
operation[i]=0;
}
color[0]=1;//(0,0)
d[0]=0;
queue<int> Q;
Q.push(0);
while(!Q.empty())
{
int u=Q.front();
Q.pop();
int v[2];
v[0]=u/(B+1);//瓶A中的水容量
v[1]=u-v[0]*(B+1);//瓶B中的水容量
int i; //经过操作后,新的容量(i/(B+1),i%(B+1))
for(int j=0;j<6;j++)
{
switch(j)
{
case 0:
i=num[0]*(B+1)+v[1]; //FILL(1)
break;
case 1:
i=v[0]*(B+1)+num[1]; //FILL(2)
break;
case 2:
i=v[1]; //DROP(1)
break;
case 3:
i=v[0]*(B+1); //DROP(2)
break;
case 4:
if(v[0]+v[1]<=num[0])
i=(v[0]+v[1])*(B+1);
else
i=(num[0]*(B+1))+v[1]-(num[0]-v[0]);
break; //POUR(2,1)
case 5:
if(v[0]+v[1]<=num[1])
i=(v[0]+v[1]);
else
i=(v[0]-(num[1]-v[1]))*(B+1)+num[1];
break; //POUR(1,2)
default:
break;
}
if(color[i]==0)
{
d[i]=d[u]+1;
color[i]=1;
pi[i]=u;
operation[i]=j;
if(i/(B+1)==C || (i%(B+1))==C)
return i;
Q.push(i);
}
}
color[u]=2;
}
return -1;
}
void print_path(int s,int v)
{
if(v==s)
return;
print_path(s,pi[v]);
switch(operation[v])
{
case 0:
cout << "FILL(1)";
break;
case 1:
cout << "FILL(2)";
break;
case 2:
cout << "DROP(1)";
break;
case 3:
cout << "DROP(2)";
break;
case 4:
cout << "POUR(2,1)";
break;
case 5:
cout << "POUR(1,2)";
break;
default:
break;
}
cout << endl;
} over