在一个数组中找到第k小的数(线性时间选择)
在这一部分,我们讨论的题目为元素选择问题。这类题目的一般问法为:给定线性序集中n个元素和一个整数k,1 <= K <= n,要求找出这n个元素中第k小的元素,如(1,4,3,2,5)中第一小的元素就是1,第5小的元素就是5,第2小的元素就是2。
在某些特殊情况下,很容易设计出解选择问题的线性时间算法。如:当要选择最大元素或最小元素时,显然可以在O(n)时间完成。如果k <= n/logn,通过堆排序算法可以在O(n + klogn) = O(n)时间内找出第k小元素。当k >= n - n/logn时也一样。
一般的选择问题,特别是中位数的选择问题似乎比最小(大)元素要难。但实际上,从渐近阶的意义上,它们是一样的。也可以在O(n)时间完成。
下面我们用两种方法进行求解。
第一种:分治算法RandomizedSelect
思想:调用了随机划分函数RandomizedPartition,所以这个分治算法也是一个随机化的算法。
通过将其划分,我们逐渐可以缩小查找的范围进行查找。
时间复杂度:一般情况下为O(n),最坏情况下,数字有序且找最大的数,则为O(n)
代码:
#include<windows.h>
#include<iostream>
#include<assert.h>
#include<time.h>
#include<vector>
#include<limits.h>
using namespace std;
template<class Type>
int Partition(Type *ar,int left,int right)
{
int i = left, j = right;
Type tmp = ar[i];
while(i<j)
{
while(i<j && ar[j] > tmp) --j;
if(i<j) { ar[i] = ar[j];}
while(i<j && ar[i] <= tmp) ++i;
if(i<j) { ar[j] = ar[i];}
}
ar[i] = tmp;
return i;
}
template<class Type>
int RandPartition(Type *ar,int left,int right)
{
//Sleep(800);
srand(time(NULL));
int pos = (rand() % (right - left + 1)) + left;
swap(ar[pos],ar[left]);
return Partition(ar,left,right);
}
template<class Type>
Type SelectK(Type *ar,int left,int right,int k)
{
if(left == right && k == 1) return ar[left];
int index = Partition(ar,left,right);
int pos = index - left + 1;
if(k <= pos) return SelectK(ar,left,index,k);
else return SelectK(ar,index+1,right,k-pos);
}
第二种:中位值的中位数法,类似于第一种方法,但是在最坏情况下也可以在O(n)时间内完成选择任务的算法Select。
思想:如果能在线性时间内找到一个划分基准,使得按这个基准所划分出的2个子数组的长度都至少为原数组长度的ε倍(0<ε<1是某个正常数),那么就可以在最坏情况下用O(n)时间完成选择任务。(这里只是找到这个划分基准(中位数的中位数)的值,而不是向快速排序那样将这个基准值放到正确的位置上)
步骤:
①:将n个输入元素划分成n/5(向下取整)个组,每组5个元素,最多只可能有一个组不是5个元素。用任意一种排序算法,将每组中的元素排好序,并取出每组的中位数,共n/5(向下取整)个。
②:递归调用select来找出这n/5(向下取整)个元素的中位数。如果n/5(向下取整)是偶数,就找它的2个中位数中较大的一个。以这个元素作为划分基准。
画图示意:

例如:按递增顺序,找出下面29个元素的第18个元素:
8,31,60,33,17,4,51,57,49,35,11,43,37,3,13,52,6,19,25,32,54,16,5,41,7,23,22,46,29
(1) 这些元素可以分为(29)/5 == 5组(向下取整),并且排序。
分为这5组: (8,31,60,33,17),(4,51,57,49,35),(11,43,37,3,13),(52,6,19,25,32),(54,16,5,41,7);
排序结果:
![]()
(2) 提取每一组的中位数元素,依次放到数组最前面并排序,构成集合{13,16,25,31,49};
![]()
(3) 将放到最前面的各个小组的中位数传入递归算法中求取中位数的中位数,得到m=25;
(4) 根据m=25, 调用快速排序,先找到值为25的数位置,再将其与第一个值进行交换,以此为基准再进行正常的快速排序,最终成功把29个元素划分为了3个子数组(按原有顺序)
- P={23,17,22,16,7,4,5,8,19,6,3,11,13}
- Q={25}
- R={43,37,57,51,32,52,49,35,60,41,54,33,31,29,46}

(5) 由于P组有13个元素,Q组有1个元素,k组有18个元素,所以我们要找的第18小元素肯定不在P组和Q组内,所以放弃P,Q,使k=18-13-1=4,对R递归地执行本算法;
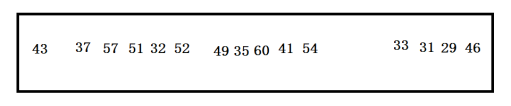
(6) 将R划分成3(floor(15/5))组:{31,60,33,51,57},{49,35,43,37,52},{32,54,41,46,29}

(7) 求取这3组元素的中值元素分别为:{43,49,33},这个集合的中值元素是43;
![]()
(8) 根据43将R划分成3组: {33,37,32,31,29,35,41},{43},{52,60,49,57,51,46,54}

(9)依次这样寻找下去,我们可以发现,几乎每次都是对半分,接近于二分法,所以效率很高,当然这个数组中中位数没有重复值,不过如果有,那么我们将中位数的重复值集中在中位数周围,如果这样的元素m >= 1,则加上一步判断:如果j <= k <= j+m-1(j为基准前数组的个数),则不必再进行递归,直接return 基准值即可,当然,这个数组中位数是没有重复值的,所以可以很快找到第十八小元素为33。
时间复杂度:设数组长度为n
当n<75时,算法select所用的计算时间不超过某一常数C1,所以直接调用其他排序算法即可。
当n≥75时,for循环执行n/5次,每次用时为某一常数;select找中位数的中位数,由于长度为原长度的1/5,所以用时可记为T(n/5);划分以后所得到数组至多有3n/4个元素,用时记为T(3n/4)。
由此,我们得到T(n)的递归式为:

解此递归式可得T(n) = O(n)。
由于我们将每一组的大小定为5,并选取75作为是否作递归调用的分界点(大于75使用该算法)。这2点保证了T(n)的递归式中2个自变量之和n/5+3n/4=19n/20=εn,0<ε<1。这是使T(n)=O(n)的关键之处。当然,除了5和75之外,还有其他选择。
注意:
①:设中位数的中位数是x,比x小和比x大的元素至少3*(n-5)/10个,原因:3*(n/5-1)*1/2
- 3---中位数比x小的每一组中有3个元素比x小
- n/5-1---有5个数的组数
- 1/2---大概有1/2组的中位数比x小
②:而当n≥75时,3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4,也就是说,长度最长为原长度的3/4。

如图,划分的左上部分肯定是要比x小的(大概占1/4)右下部分是肯定比x大的(大概占1/4)左下和右上不确定,就算这两部分同时不比x小或比x大,在极端情况下划分成的子区间也能至少缩短1/4!
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<algorithm>
using namespace std;
void bubbleSort(int a[],int p,int r){
for(int i=p;i<r;i++){
for(int j=i+1;j<=r;j++){
if(a[j]<a[i])swap(a[i],a[j]);
}
}
}
int Partition(int a[],int p,int r,int val){
int pos;
for(int q=p;q<=r;q++){
if(a[q]==val){pos=q;break;}
}
swap(a[p],a[pos]);
int i = p, j = r;
int tmp = ar[i];
while(i<j)
{
while(i<j && ar[j] > tmp) --j;
if(i<j) { ar[i] = ar[j];}
while(i<j && ar[i] <= tmp) ++i;
if(i<j) { ar[j] = ar[i];}
}
ar[i] = tmp;
return i;
}
int Select(int a[],int p,int r,int k){
if(r-p<75){
bubbleSort(a,p,r);
return a[p+k-1];
}
for(int i=0;i<=(r-p-4)/5;i++){//把每个组的中位数交换到区间[p,p+(r-p-4)/4]
int s=p+5*i,t=s+4;
for(int j=0;j<3;j++){//冒泡排序,从后开始排,结果使得后三个数是排好顺序的(递增)
for(int n=s;n<t-j;n++){
if(a[n]>a[n+1])swap(a[n],a[n-1]);
}
}
swap(a[p+1],a[s+2]);//交换每组中的中位数到前面
}
//(r-p-4)/5表示组数-1,则[p,p+(r-p-4)/5]的区间长度等于组数
int x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//求中位数的中位数
int i=Partition(a,p,r,x),j=i-p+1;
if(k<=j)return Select(a,p,i,k);
else return Select(a,i+1,r,k-j);
}参考博客:https://blog.csdn.net/m0_37579232/article/details/80178000