有趣的组合数学题;考试时候打满确实挺不容易的……
题目描述
对于一个 $n$ 阶排列 $p$,我们建立一张无向简单图 $G(p)$,有 $n$ 个节点,标号从 $1$ 到 $n$,每个点向左右两侧最近的比它大的点以及比它小的点连边。 形式化地,在 $G(p)$ 中,$\forall u<v$,边 $(u,v)$ 存在当且仅当以下四个条件至少一个成立:
-
$p_u<p_v$,且不存在 $u<i<v$ 满足 $p_u<p_i$;
-
$p_u>p_v$,且不存在 $u<i<v$ 满足 $p_u>p_i$;
-
$p_u<p_v$,且不存在 $u<i<v$ 满足 $p_i<p_v$;
-
$p_u>p_v$,且不存在 $u<i<v$ 满足 $p_i>p_v$。
现在在所有的 $n$ 阶排列中随机选择一个排列 $p$,请求出 $G(p)$ 中三元简单环的期望个数,答案对 $998244353$ 取模。
数据规模与约定
对于所有数据,$1\le n<998244353$。
题目分析
基础的暴力
首先会有个$(C^3_n)^2$的想法:枚举所有的三元环位置以及三个位置各是什么数,再根据这来统计每个三元环的合法贡献。
观察性质:从零开始推式子
由于这题有非常特殊的建边性质,所以可以先来考虑怎么样形态的三元组才是合法的。
容易发现,三元环的极值一定是在中间点,那么就只存在四种形态的三元组。同时,这四种形态的三元环具有很好的对称性,所以它们方案数是相同的。
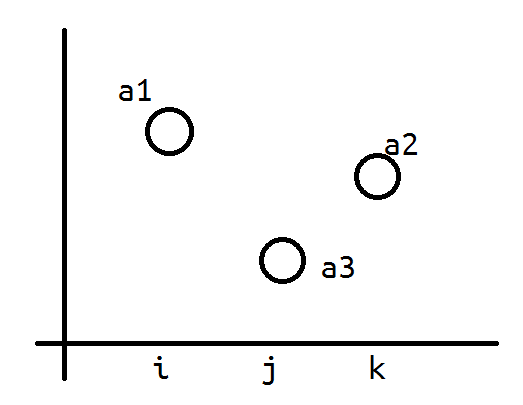
下面只考虑一种情况如上图所示。在这种情况下,想要三点间都存在边只能是能让$\max a_{i...k} < a3$.
接下去从最暴力的式子开始推起:
$\sum_{i=1}^{n-2}{n-i\choose2}\sum_{k_1+k_2<i}{i-1\choose k_1}{i-1-k_1\choose k_2}k_1!k_2!(n-k_1-k_2-3)!(n-k_1-k_2-2)$
其中i表示枚举a1的取值;k1,k2表示a1...a3,a3...a2之间夹的数的个数。最后的一项$(n-k_1-k_2-2)$表示将i...k这些数看作一个整体,插空在其他数里的方案数。
END