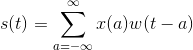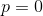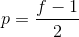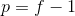目录
如果这篇文章对你有一点小小的帮助,请给个关注,点个赞喔~我会非常开心的~
花书+吴恩达深度学习(十二)卷积神经网络 CNN 之全连接层
花书+吴恩达深度学习(十三)卷积神经网络 CNN 之运算过程(前向传播、反向传播)
花书+吴恩达深度学习(十四)卷积神经网络 CNN 之经典案例(LetNet-5, AlexNet, VGG-16, ResNet, Inception Network)
0. 前言
卷积神经网络(convolutional neural network,CNN)是一种专门用来处理具有类似网格结构的数据的神经网络。
卷积网络是指那些至少在网络中的一层使用卷积运算来替代一般矩阵乘法的神经网络。
数学意义上的离散卷积表示如下:
其中, 
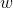
在数学中,在计算卷积之前需要对过滤器进行翻转。
在机器学习中,计算方式和卷积一样,只是没有翻转,称为互相关函数,但是通常称之为卷积。
1. 2D 图像卷积
卷积运算如下图所示(图源:深度学习):

过滤器(核函数)像是依次扫描图像二维矩阵的窗口,将对应位置相乘再相加。
如果原始图像的大小为 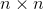

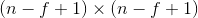
2. 3D 图像卷积
卷积不仅仅适用于 2D 的图像,而且还可以用于 3D 的图像中。
一个彩色的图像,除了长和宽以外,还有 RGB 图像值,称为通道数(channel),这三个组成了 3D 图像。
在对 3D 图像进行卷积的时候,过滤器也应该是 3D 的,且通道数要与原图像一致。
如下图所示(图源:吴恩达深度学习):

过滤器像一个立方体,依次扫描原图像,所以最后卷积的结果为 2D 图像。
3. 过滤器(核函数)
在计算机视觉中,通常过滤器大小 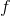
过滤器中的参数,通常有几种选择方式:
- 手动设计参数,例如边缘检测的参数
- 随机初始化参数
- 通过监督训练,在反向传播的迭代过程中自动修改参数
4. 过滤器应用于边缘检测
如下图所示(图源:吴恩达深度学习),数字更高代表像素点更亮:

原图像与过滤器卷积后,得到的结果,可看作原图像的中间边缘检测。
如果过滤器是左边表示亮色(1),右边表示暗色(-1),那么卷积出来的结果,如果是正的边,代表原图像左边像素比右边像素亮(与过滤器相同),如果是负的边,代表原图像左边像素比右边像素暗(与过滤器相反)。水平边沿检测同理可得。
在 3D 卷积中,如果想仅仅检测红色通道(R)的边缘,则可以使得过滤器 R 层为边缘检测的参数,而其他层为 0 。
通常在神经网络中,可以将过滤器的设定为可调的参数,然后在训练神经网络的时候,对其自动进行修改。
这样的神经网络可以通过多个过滤器,学习不同角度的边缘,就可以学习到一些低层次的特征。
每个过滤器可看作一个神经元,多个神经元组成了神经网络的一层。
将每一个过滤器叠加在一起,组成高层次的特征作为下一层的输入。
5. padding 填充
padding 是指,在卷积运算之前先对原始图像的周围进行填充像素 0 。
使用 padding 的原因主要有:
- 通过卷积运算会导致图片缩小,如果神经网络很深的话,图片在最后会被缩的很小
- 根据卷积移动窗口,原图像中间的像素点会被重复计算很多次,而边沿的像素点则只会计算很少次,这就造成边沿信息的丢失
而 padding ,使得原图像扩大,同时也使得原始图像边沿的信息可以被多次计算到。
周围每边填充的像素大小为 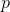

选择 padding 大小的策略:
- valid 有效卷积:不进行 padding 填充,
- same 相同卷积:使得卷积后的图像大小和原图像大小相同,
- full 全卷积:添加足够多的
,使得每个像素都被访问了
次,输出大小为
,
通常 padding 的最优数量处于有效卷积和相同卷积之间的某个位置。
6. stride 步长
上述在进行卷积运算的时候,过滤器窗口每次只平移扫描一格,现在平移 

如果原始图像大小为 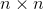
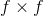
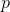

7. 使用卷积的动机
如果直接使用前馈神经网络的矩阵计算,那么在图像大的时候,参数的数量级是很高的。
例如,第一层 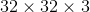
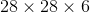
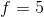
如果采用矩阵计算,参数大小是 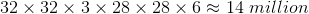
如果采用卷积计算,则参数大小是 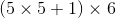
卷积运算通过三个重要思想改善了机器学习系统:
- 稀疏交互(sparse interactions):在矩阵计算中,每一个神经元都与这层所有的输入产生交互;而在卷积计算中,每一个神经元仅与输入的图像中对应位置的过滤器大小的区域产生交互。减少了模型的存储需求,减少了计算量,虽然卷积运算直接连接是稀疏的,但是在更深的层中单元可以间接的连接到大部分输入
- 参数共享(parameter sharing):如果一个特征检测器对图像中的某一区域有效果,可能也会对图像中的另一个区域有效果。参数共享保证了我们只需要学习一个参数集合,而不是对每一个输入都需要学习一个参数
- 等变表示(equivariant representations):如果一个函数满足输入改变,输出也以同样的方式改变,就说它是等变的,如果函数
满足
,那么它们具有等变性。例如,对输入先进行平移变换然后再卷积,和先对输入卷积然后再对输出平移变换,结果是一样的
8. 1乘1卷积
1乘1 卷积是指过滤器的大小是 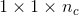
对于单个通道的输入来说,就等效于将输入的每个单元乘以一个值。
对于多个通道的输入来说,就等效于将同个单元的不同通道上的数值乘以过滤器对应通道上的数值,然后相加。
对于多个通道来说,这是一种压缩通道的方式,经过这个神经元输出为 2D 的图像,然后可通过不同的过滤器,叠加输出,成为新的 3D 图像。
9. 基本卷积函数的变体
已知,矩阵运算如下图所示(图源:深度学习):

已知,卷积运算如下图所示(图源:深度学习):

有时,我们并不是想使用卷积,而是想用一些局部连接的网络层。
非共享卷积(局部连接层)(unshared convolution),是局部连接,但不共享参数的运算。
当每一个特征都是一小块空间,并且相同的特征不会出现在所有的空间上时,局部连接层很有用。
局部连接层(非共享卷积)如下图所示(图源:深度学习):

平铺卷积(tiled convolution),对卷积层和局部连接层进行折中。
平铺卷积并不是对每一个空间位置的权重进行学习,而是学习一组的过滤器,然后循环使用这组过滤器。
平铺卷积如下图所示(图源:深度学习):

如果这篇文章对你有一点小小的帮助,请给个关注,点个赞喔~我会非常开心的~