详细推导PCA算法（包括算法推导必备的知识）

本文主要思路如下：

1 PCA优化目标

PCA（主成分分析）是一种数据降维的方法，即用较少特征地数据表达较多特征地数据（数据压缩，PCA属于有损压缩）。PCA推导有两种主要思路：

1. 最大化数据投影后的的方差（让数据更分散）
2. 最小化投影造成的损失

本文采用第一种思路完成推导过程，下图中旋转的是新坐标轴，每个数据点在改坐标轴上垂直投影，最佳的坐标轴为数据投影后的数据之间距离最大。

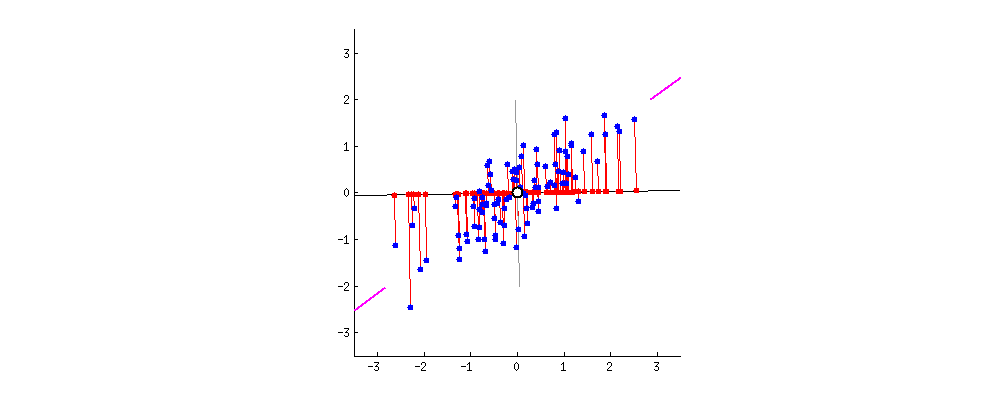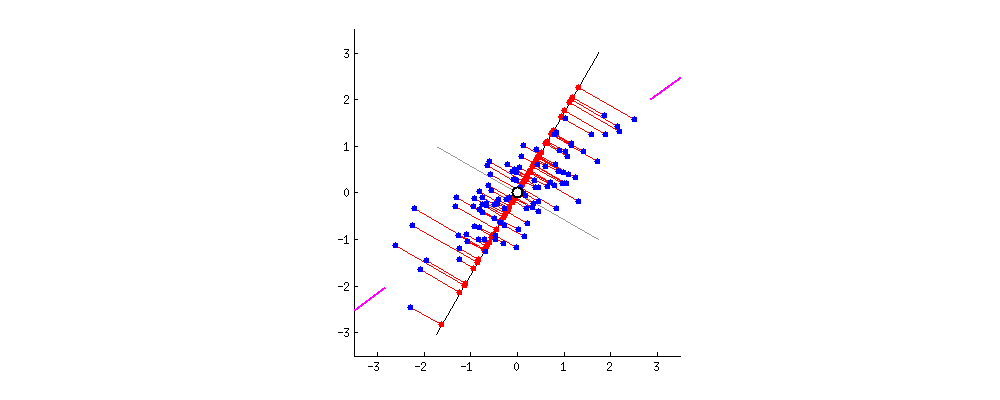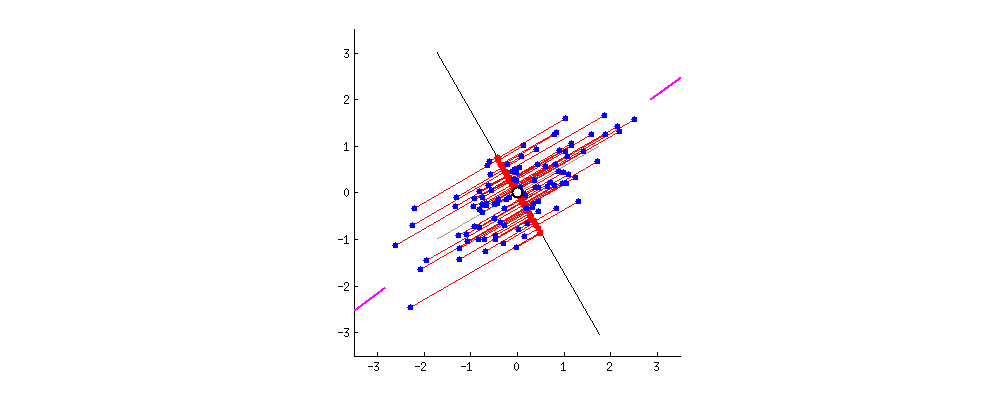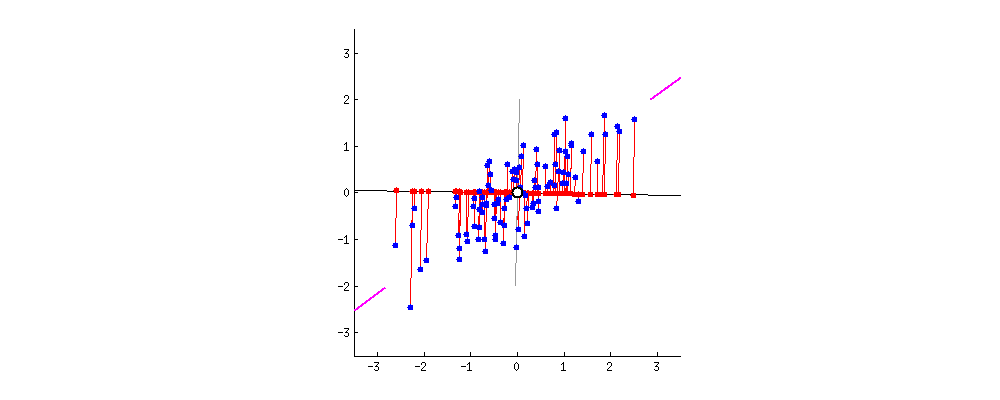
要完成PCA推导过程，需要如下第 2 章部分的理论依据

2 理论依据

2.1 矩阵换基底

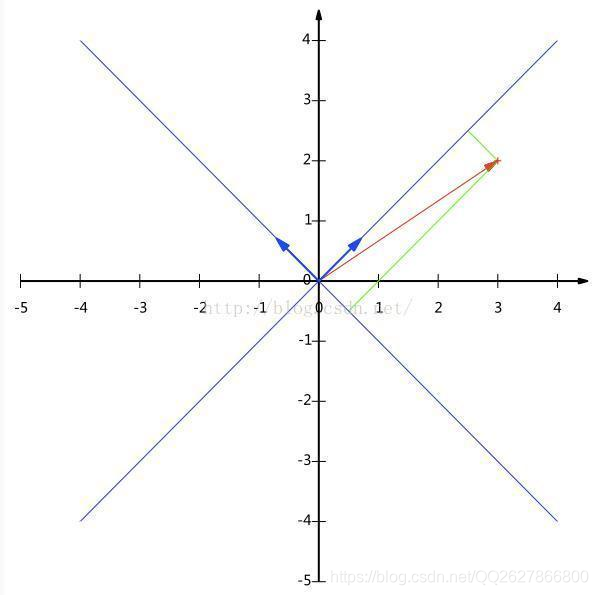
坐标变换地目标是，找到一组新的正交单位向量，替换原来的正交单位向量。下面通过具体例子说明。
假设存在向量 $\vec{a}=\begin{bmatrix} 3\\2\end{bmatrix}$ ，要变换导以 $\vec{u}=\begin{bmatrix}{1\over\sqrt{2}}\\ {1\over\sqrt{2}}\end{bmatrix}$, $\vec{v}=\begin{bmatrix}-{1\over\sqrt{2}}\\ {1\over\sqrt{2}}\end{bmatrix}$ 为新基底地坐标上，求在心坐标系中的坐标

$\because$ 向量 $\vec{a}$ 在向量 $\vec{u}$ 上的投影距离 s：
$s=||\vec{a}||\cdot \cos\theta = {\vec{a}\cdot\vec{u}\over ||\vec{u}||}=\vec{a}\cdot\vec{u}$
其中： $\theta$ 表示两个向量之间的夹角
$\therefore a_u=\vec{u}^T\cdot \vec{a},\ a_v=\vec{v}^T\cdot \vec{a}\\$

$\therefore$ 向量 $\vec{a}$ 在新坐标系中的坐标可以表示为：
$\vec{a}_{new} =\begin{bmatrix}\vec{u}&\vec{v}\end{bmatrix}^T\cdot \vec{a} =\begin{bmatrix} \vec{u}^T\cdot\vec{a}\\ \vec{v}^T\cdot\vec{a}\\ \end{bmatrix}\\$
如果矩阵 A 的列向量分别表示原来坐标系中的点，那么在新坐标系中的坐标为：
$A_{new} =\begin{bmatrix}\vec{u}&\vec{v}\end{bmatrix}^T\cdot A\\$
如果 $\vec{a}_{center}$ 表示一系列数据点的中心，那么可以证明：
$\vec{a}_{newcenter}=\begin{bmatrix}\vec{u}&\vec{v}\end{bmatrix}^T\cdot \vec{a}_{center}\\$
经过上面的变换之后，新坐标系相比原坐标系顺时针旋转了45度； $\vec{a}$ 相对新坐标系位置和相对原坐标系位置发生了逆时针旋转45度。即：上述变换过程为向量的旋转过程，旋转的角度=-坐标系旋转角度

如果 $||\vec{u}||\neq1, ||\vec{v}||\neq 1$ ，那么：
$\vec{u}^T\cdot \vec{a}=s\cdot ||\vec{u}||\\ \vec{v}^T\cdot \vec{a}=s\cdot ||\vec{v}||\\$
即： $\vec{a}_{new}$ 相比 $\vec{a}$ ，2个坐标分别放大了 $||\vec{u}||$ 倍和 $||\vec{v}||$ 倍。即向量发生了伸缩。

2.2 拉格朗日乘子法

拉格朗日乘子法主要提供了一种求解函数在约束条件下极值的方法。下面还是通过一个例子说明。
假设存在一个函数 $f(x,y)$ ，求该函数在 $g(x,y)=c$ 下的极值（可以是极大，也可以极小）

通过观察我们发现，在极值点的时候两个函数必然相切，即此时各自的导数成正比，从而：
${\partial f\over\partial x}=\lambda{\partial g\over\partial x}\\ \ \\ {\partial f\over\partial y}=\lambda{\partial g\over\partial y}\\ \ \\ g(x,y)=c\\$
通过联立上述三个公式，既可以求出最终结果。拉格朗日算子的主要思路同上，不过他假设了一个新的函数：
$F(x,y,\lambda)=f(x,y)+\lambda[c-g(x,y)]\\$
然后分解求：
${\partial F\over\partial x}=0\\ \ \\ {\partial F\over\partial y}=0\\ \ \\ {\partial F\over\partial \lambda}=0\\$
从而完成求解过程

2.3 协方差矩阵

假设有一组数据：
$\begin{array}{c|cccc} 样本编号&变量x（如发传单数量）&变量y（如购买数量）&变量z（如购买总价）\\ \hline 1& 1 &2&3\\ 2&35&25&55\\ \cdots&\cdots&\cdots&\cdots\\ \end{array}$
协方差研究的目的是变量（特征）之间的关系，也就是上表中的发传单数量、购买数量、购买总额之间的相关情况
上表数据用矩阵表示为：
$X=\begin{bmatrix} 1&35&\cdots\\ 2&25&\cdots\\ 3&55&\cdots\\ \end{bmatrix}\\$
那么两两变量之间的关系：
$cov(x,y)=E[(1-E(x))(2-E(y))+(35-E(x))(25-E(y))+\cdots]\\ cov(x,z)=E[(1-E(x))(3-E(z))+(35-E(x))(55-E(z))+\cdots]\\ \cdots\\$
如果 $E(x)=E(y)=E(z)=0$（可以通过数据初始化实现），那么上述的协方差关系可以用如下矩阵乘法表示：
$cov(X)={1\over m}XX^T=\begin{bmatrix} cov(x,x)&cov(x,y)&cov(x,z)\\ cov(y,x)&cov(y,y)&cov(y,z)\\ cov(z,x)&cov(z,y)&cov(z,z)\\ \end{bmatrix}\\$
如果把对角线上的数据加起来会发现：
$cov(x,x)+cov(y,y)+cov(z,z)=E[([(1-E(x)]^2+[2-E(y)]^2+[3-E(z)]^2)+\cdots]={1\over m}\sum_{i=1}^m||X_i-X_{center}||^2\\$
也就是说每个样本点到样本中心距离的平方和的平均 = 样本各个特征方差和（自身协方差）= ​ $\sum diag({1\over m}XX^T)$ ，即样本的方差

2.4 特征向量和奇异值分解

2.4.1 特征向量

参考：特征值和特征向量

假设：左侧矩形由 $\begin{bmatrix} \vec{i}&\vec{j} \end{bmatrix}=\begin{bmatrix} 1&0\\ 0&1\\ \end{bmatrix}$ 定义，右侧矩形由 $\begin{bmatrix} \vec{i'}&\vec{j'} \end{bmatrix}=\begin{bmatrix} 2&0\\ 0&0.5\\ \end{bmatrix}$ 定义。

根据 2.1 矩阵拉伸变换的结果，变换矩阵 $A=\begin{bmatrix} \vec{u}^T\\ \vec{v}^T\\ \end{bmatrix}=\begin{bmatrix} 2&0\\ 0&0.5\\ \end{bmatrix}$ ，即：
$A\cdot\begin{bmatrix} \vec{i}&\vec{j} \end{bmatrix}=\begin{bmatrix} \vec{i'}&\vec{j'}\\ \end{bmatrix}\\$
在应用变换矩阵变换时，我们发现存在与上图中红色向量平行的向量 \vec{a} ，他们总满足：
$A\cdot \vec{a}\ \ \ //\ \ \ \vec{a}\\$
即：
$A\cdot \vec{a}=\lambda\cdot \vec{a}\\$
所以：红色的特征向量不受变换矩阵的影响，仍保持原来的方向，我们称这类向量为变换矩阵A的特征向量，对应的 \lambda 为特征值。又因为特征向量有很多个，即：
$A\cdot \vec{a_i}=\lambda_i\cdot \vec{a_i}\\$
所以：
$A\cdot\begin{bmatrix} \vec{a_1}&\vec{a_2}&\cdots \end{bmatrix}=\begin{bmatrix} \vec{a_1}&\vec{a_2}&\cdots \end{bmatrix}\cdot\begin{bmatrix} \lambda_1&&\\ &\lambda_2&\\ &&\ddots \end{bmatrix}\Rightarrow A=Q\cdot \Sigma\cdot Q^{-1}\\$
其中：Q的列向量都是A变换矩阵的特征向量
另外，在做旋转变换时，要求变换前后的坐标维度不发生改变，即A须为方阵
综上：如果方阵A满足 $A=Q\cdot \Sigma\cdot Q^{-1}$ ，那么Q为特征向量， $\Sigma$ 为对应的特征值

2.4.2 奇异值分解

奇异值分解（svd: singular value decomposition）定义：对于任意的矩阵A，存在：
$A_{m\times n}=U_{m\times m}\cdot\Sigma_{m\times n}\cdot V_{n\times n}^T\\$
其中：
$U^T\cdot U=I_m\\ V^T\cdot V=I_n\\$
即：U的列向量两两正交且模为1，V列向量两两正交且模为1，即：
$U^T=U^{-1}\\ V^T=V^{-1}\\$

2.4.3 特征向量和奇异值分解的关系

对于任意矩阵 A ，对A做svd有：
$AA^T=U\Sigma V^T\cdot V\Sigma U^T=U\Sigma^2U^{-1}\\$
令 $\Sigma'=\Sigma^2$ ，则：
$AA^T=U\Sigma' U^{-1}\\ 满足A=Q\Sigma Q^{-1}特征向量定义\\$
所以 AA^T 能实现特征分解，又因为：
$AA^T=\underbrace{U''\Sigma'' V''^T}_{svd}\\$
所以：
$U=U''\\ \Sigma'=\Sigma''\\ U^{-1}=V''^T\Rightarrow U=V''$
因此：对 $AA^T$ 做SVD，那么得到的U’'列向量为特征向量（对应A的U矩阵）， $\Sigma''$ 为特征值对角阵

同理：对 $A^TA$做SVD，那么得到的U’'列向量为特征向量（对应A的V矩阵）， $\Sigma''$ 为特征值对角矩阵

3 PCA

3.1 PCA推导

PCA的目标是找到一组新的正交基 $\{u_1,u_2,\cdots,u_k\}$ （从n维下降到k维），使得数据点在该正交基构成的平面上投影后，数据间的距离最大，即数据间的方差最大。如果数据在每个正交基上投影后的方差最大，那么同样满足在正交基所构成的平面上投影距离最大。

根据2.1，设正交基 $u_j$ ，数据点 $x_i$ 在该基底上的投影距离为 $x_i^T\cdot u_j$ ，所以所有数据在该基底上投影的方差 $J_j$ 为：
$J_j={1\over m}\sum_{i=1}^m(x_i^Tu_j-x_{center}^Tu_j)^2\\$
其中：m为样本数量，在数据运算之前对数据 x 进行0均值初始化，即 x_{center}=0 ，从而：
$J_j={1\over m}\sum_{i=1}^m(x_i^Tu_j)^2 ={1\over m}\sum_{i=1}^m(u_j^Tx_i\cdot x_i^T u_j) =u_j^T\cdot {1\over m}\sum_{i=1}^m(x_ix_i^T)\cdot u_j \\$
所以：
$J_j =u_j^T\cdot {1\over m}(x_1x_1^T+x_2x_2^T+\cdots+x_mx_m^T)\cdot u_j =u_j^T\cdot {1\over m}(\begin{bmatrix}x_1&\cdots&x_m\end{bmatrix}\cdot\begin{bmatrix}x_1\\ \vdots \\x_m\end{bmatrix})\cdot u_j =={1\over m}u_j^TXX^Tu_j\\$
由于 ${1\over m}XX^T$ 为常数，这里假设 $S={1\over m}XX^T$ ，则： $J_j=u_j^T\cdot S\cdot u_j$ ，根据PCA目标，我们需要求解 $J_j$ 最大时对应的 $u_j$
根据 2.2 中的拉格朗日算子（求极值）求解：
$J_{j}=u_j^TSu_j\\\ \\s.t.\ u_j^Tu_j=1\\$
则构造函数：
$F(u_j)=u_j^TSu_j+\lambda_j(1-u_j^Tu_j)\\$
求解 ${\partial F\over\partial u_j}=0$ ，得：
$2S\cdot u_j-2\lambda_j\cdot u_j=0\ \ \Rightarrow\ \ Su_j=\lambda_ju_j\\$
结合2.4.1则：当 $u_j、\lambda_j$ 分别为S矩阵的特征向量、特征值时， $J_j$ 有极值，把上述结果带回公式得：
${J_j}_m=u_j^T\lambda_j u_j=\lambda_j\\$
所以对于任意满足条件的正交基，对应的数据在上面投影后的方差值为S矩阵的特征向量，从而：
$J_{max}=\sum_{j=1}^k \lambda_j，\lambda从大到小排序\\$
所以投影正交基为S的特征向量中的前k个最大特征值对应的特征向量。
接下来对S进行特征分解，根据2.4.3特征向量和svd的关系结论，S的特征向量集合：
$U = U\ of\ svd(S)=U\ of\ svd({1\over m}XX^T)\\$
另外，由于 $S={1\over m}XX^T$ 由于X已0均值处理，根据2.3 协方差矩阵定义：S为数据集X的协方差矩阵。
综上，即可得到满足投影后数据距离最大的新的正交基 $\{u_1,u_2,\cdots,u_k\}$
因此：
$X_{new_{k\times m}}=\begin{bmatrix} u_1^T\\ u_2^T\\ \vdots\\ u_k^T\\ \end{bmatrix}_{k\times n}\cdot X_{n\times m}\\$

3.2 PCA过程总结

PCA流程如下：

1. 初始化X，使得所有样本之间的特征值均值为0，同时应用feature scaling，缩放到-0.5～0.5 ;
2. 计算X的协方差矩阵S;
3. 对S进行SVD分解，U即我们要求的新坐标系集合， $\Sigma$ 为特征值集合（计算时特征值都会大于0，且结果会从小到大排列）;
4. 按照特征值从大到小排序，要降低为k维，那么取前k个特征值对应的特征向量，就是新的k个坐标轴
5. 把X映射到新的坐标系中，完整降维操作;

根据之前的公式，做PCA投影后，投影数据的方差：
$Var_{X_{project}}=\sum_{j=1}^kJ_j=\sum_{j=1}^k\lambda_j\\$
又因为：数据从n维投影新的n维的坐标系，方差不会发生改变（向量的模长度相等且为1，可以用2D坐标系投影到45-135度坐标系验证），即：
$Var_X=Var_{X_{project}}=\sum_{j=1}^nJ_j=\sum_{j=1}^n\lambda_j\\$
即：X的协方差矩阵的特征值和对应X的方差