1 信息量
- 定义:信息量是对信息的度量。
就跟时间的度量是秒一样,当我们考虑一个离散的随机变量x的时候,当我们观察到的这个变量的一个具体值的时候,我们接收到了多少信息呢? - 多少信息用信息量来衡量,我们接受到的信息量跟具体发生的事件有关。
- 信息的大小跟随机事件的概率有关。
越小概率的事情发生了产生的信息量越大,如湖南产生的地震了;越大概率的事情发生了产生的信息量越小,如太阳从东边升起来了,其实代表着没有任何信息量。 - 一个具体事件的信息量应该是随着其发生概率而递减的,且不能为负。
- 如果我们有俩个不相关的事件x和y,那么我们观察到的俩个事件同时发生时获得的信息应该等于观察到的事件各自发生时获得的 信息之和,即:
\(h(x,y) = h(x) + h(y)\). - 由于x,y是俩个不相关的事件,那么满足 \(p(x,y)=p(x)p(y)\). 根据上面推导,可以看出: \(h(x)\) 一定与\(p(x)\)的对数有关,因此我们有信息量公式如下:
\(h(x) = -\log_2p(x)\). - 思考两个问题:
- 为什么有负号?
- 为什么底数是2?
2 信息熵
- 定义:用来度量信息的不确定程度。
- 解释: 熵越大,信息量越大。不确定程度越低,熵越小,比如“明天太阳从东方升起”这句话的熵为0,因为这个句话没有带有任何信息,它描述的是一个确定无疑的事情。
公式:
\[H(X) = -\sum_{i=1}^n p(x_i)\log{p(x_i)}\]2.1 举个例子
- 题目:假设有随机变量X,用来表达明天天气的情况。X可能出现三种状态 1) 晴天2) 雨天 3)阴天。每种状态的出现概率均为P(i) = 1/3,那么根据熵的公式,可以计算得到:\(H(X) = - 1/3 * log(1/3) - 1/3 * log(1/3) - 1/3 * log(1/3) = 0.47712(10为底)\)。如果log以2为底得到的结果是1.58496。
- 关于“熵”不同的教材会有所区别,例如2、10、e为底,事实上影响的是“单位”,为了统一单位,使用换底公式进行调换。
- 如果这三种状态出现的概率为(0.1, 0.1, 0.8), 那么 \(H(X) = -0.1 * log(0.1) * 2 - 0.8 * log(0.8) = 0.27753\),以2为底的结果是:0.92193。
- 可以发现前面一种分布X的不确定程度很高,每种状态都很有可能。后面一种分布,X的不确定程度较低,第三种状态有很大概率会出现。 所以对应前面一种分布,熵值很高,后面一种分布,熵值较低(2为底)。
信息熵还可以作为一个系统复杂程度的度量,如果系统越复杂,出现不同情况的种
类越多,那么他的信息熵是比较大的。如果一个系统越简单,出现情况种类很少(极端情况为1种情况,那么对应概率为1, 那么对应的信息熵为0),此时的信息熵较小。
3 条件熵
- 在一个条件下,随机变量的不确定性。
- \(H(X|Y) = -\sum_{x=0,1,2;y=0,1}^{x,y}p(x,y)\log{p(x|y)}\)。
- 具有先后性。
4 信息增益
- 信息增益 = 熵 - 条件熵。
- 信息增益越大,机器学习越精准,loss越小。
- 信息增益的应用: 我们在利用进行分类的时候,常常选用信息增益更大的特征,信息增益大的特征对分类来说更加重要。决策树就是通过信息增益来构造的,信息增益大的特征往往被构造成底层的节点。
5 互信息
- 定义:指两个随机变量之间的相关程度。
- 理解:确定随机变量X的值后,另一个随机变量Y不确定性的削弱程度,因而互信息取值 最小为0,意味着给定一个随机变量对确定一另一个随机变量没有关系,最大取值为随机变量的熵,意味着给定一个随机变量,能完全消除另一个随机变量的不确定性。这个概念和条件熵相对。
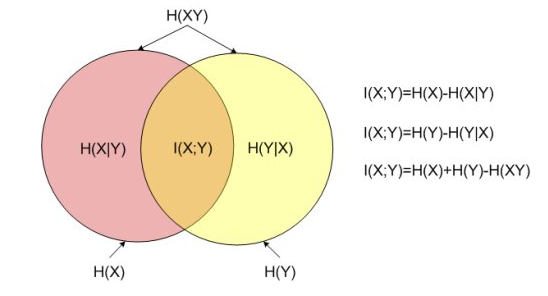
- 公式:\(I(X;Y)=H(X)-H(X|Y)\)
- 经过推导后,我们可以直观地看到H(X)表示为原随机变量X的信息量,H(X|Y)为 知道事实Y后X的信息量,互信息I(X;Y)则表示为知道事实Y后,原来信息量减少 了多少。
- 假设X,Y完全无关,H(X) = H(X|Y) , 那么I(X;Y) = 0 假设X,Y完全相关,H(X|Y) =0, 那么I(X;Y) = H(X) 条件熵越大,互信息越小,条件熵越小,互信息越大。
- 互信息和信息增益实际是同一个值。
6 交叉熵
- 如果使用估计的分布q来表示来自真实分布p的平均编码长度,则:
- \(H(p,q)=-\sum_{x}p(y)\log{q(x)}\).
- 注意与联合熵区别。
- 假如X为一组已知的输入特征值,Y为一组已知的输出分类。优化的目标是为了找到一个映射模型F, 使得预测值Y_ = F(X)与真值Y最相似。但现实世界的Y和Y_的分布肯定不是完全一致的。
所以:- Y 服从p分布(即真实分布)。
- Y_ 服从q分布。
- 交叉熵cross_entropy即为描述p,q两个分布差异性的指标。
- 因为我们编码的样本来自于真实的分布p,所以乘的是真实概率。在图像分类的时候, 比如softmax分类器,在训练的时候,我们已经给定图像的标签,所以这个时候每幅图 片的真实概率就是1,这个时候的损失函数就是:
\[ H(p,q) = -\sum_i\log(q_i) \] 交叉熵要大于等于真实分布的信息熵(最优编码)。
思考:
根据上面的叙述,我们了解到:信息论中,对于孤立的一个随机变量我们可以用熵来量化;对于两个随机变量有依赖关系,我们可以用互信息来量化。那么:对于两个随机变量之间相差多少?也就是说,这两个随机变量的分布函数相似吗?如果不相似,那么它们之间差可以量化吗?
7 相对熵
- 由交叉熵可知,用估计的概率分布所需的编码长度,比真实分布的编码长,但是 长多少呢?这个就需要另一个度量,相对熵,也称KL散度。
- 公式: \(D(p||q)=H(p,q)-H(p)=\sum_{i=1}^n p_i\log{\frac{p_i}{q_i}}\)
8 总结
- 信息熵是衡量随机变量分布的混乱程度,是随机分布各事件发生的信息量的期望值, 随机变量的取值个数越多,状态数也就越多,信息熵就越大,混乱程度就越大。当随机分布为均匀分布时,熵最大;信息熵推广到多维领域,则可得到联合信息熵H(X,Y); 条件熵表示的是在X给定条件下,Y的条件概率分布的熵对X的期望。
- 交叉熵可以来衡量在给定的真实分布下,使用非真实分布所指定的策略消除系统的不确定性所需要付出的努力的大小。
- 相对熵可以用来衡量两个概率分布之间的差异。
或者: - 信息熵是传输一个随机变量状态值所需的比特位下界(最短平均编码长度)。
- 交叉熵是指用分布q来表示真实分布p的平均编码长度。
- 相对熵是指用分布q来表示分布p额外需要的编码长度。