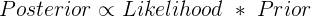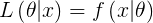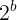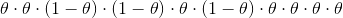前言

前面《EM概率统计基础（一）》简单讲解了后验概率和先验概率之间的关系，得到如下结果：

先验概率乘以似然函数，正比于后验概率

$\large Posterior\propto Likelihood\;\ast\;Prior$

那么似然函数是什么，它和概率又有什么关系，希望可以总结总结。

似然函数

Likelihood Function

似然函数也称为似然，是一个关于统计模型参数的函数，也就是这个函数中自变量统计模型的参数。似然函数是关于统计参数的函数，可以用来评估一组统计的参数。

似然函数的定义，它是给定联合样本值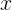 $\large x$ 下关于（未知）参数 $\large \theta$ 的函数

$\large L\left(\theta|x \right )=f\left(x|\theta \right )$

$\large x$ 表示联合样本随机变量 $\large X$ 取到的值，即 $X=x$ ；

$\large \theta$ 是指未知参数，它属于参数空间；

$\large f\left(\theta|x \right )$ 是一个密度函数，它表示（给定） $\large \theta$ 下关于联合样本值 $\large x$ 的联合密度函数

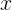
所以从定义上可以看出似然函数和密度函数完全两个数学对象：前者是关于 $\large \theta$ 的函数，后者是关于 $\large x$ 的函数。这里的等号 = 可以理解成函数值形式的相等，而不是两个函数本身是同一个函数。

似然和概率的区别

首先给出一个简便的区分方法，根据定义：

“xxxx的概率”中xxxx只能是概率空间中的事件，即事件（发生）的概率是多少，因为时间具有概率结构从而刻画随机性，所以才能谈概率

“xxxx的似然”中xxxx只能是参数，比如说上文所述的参数等于 $\large \theta$ 时的似然是多少。

举个栗子：

已知一个硬币是均匀的（在抛的过程中，正反面的概率相等），那连续10次正面朝上的概率是多少，这是一个概率问题。

如果一个硬币在10次抛落中均正面朝上，那硬币的是均匀的（在抛落中，正反面的概率相等）概率是多少，此时的概率是似然。

Probability is used before data are available to describe possible future outcomes given a fixed value for the parameter (or parameter vector).

Likelihood is used after data are available to describe a function of a parameter (or parameter vector) for a given outcome.
The likelihood of a set of parameter values, θ, given outcomes x, is equal to the probability of those observed outcomes given those parameter values, that is

有趣的栗子

这个栗子摘自Quora上一个计算机系教授的回答，很有意思。

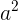
其将概率密度函数和似然函数之间类比成 $\large 2^a$ 与 $\large a^2$ 之间的关系。

假设一个函数为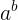 $\large a^b$ 的函数，这个函数包含两个变量。

如果设置b = 2，那么可以得到一个关于a的二次函数，即 $\large a^2$

如果设置为a = 2 ，那么将得到一个指数函数，即 $\large 2^b$

可以看出，这两个函数虽然有着不同的名字，但源自于同一个函数 $\large a^b$

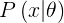
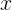
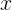
同样的， $\large P\left(x|\theta \right )$ 也是一个具有两个变量的函数，如果你将 $\large \theta$ 设置为常量，那么你可以得到一个Probability Function（function of $\large x$ ），但如果你设置 $\large x$ 为常量，那么你可以得到一个Likelihood Function（function of $\large \theta$ ）

以下举一个栗子（没错，我超喜欢吃栗子的）

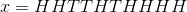
有一个硬币，它有 $\large \theta$ 的概率会正面向上，那么也就有1- $\large \theta$ 的概率会反面向上。 $\large \theta$ 存在但未知。此时，你为了获得 $\large \theta$ 的具体数值，你决定做实验：抛这枚硬币10次，得到一个序列 x=HHTTHTHHHH 。

通过概率论基础我们可以得出，出现此序列的概率为： $\theta\cdot\theta\cdot\left(1-\theta \right )\cdot\left(1-\theta \right )\cdot\theta\cdot\left(1-\theta \right )\cdot\theta\cdot\theta\cdot\theta\cdot\theta$