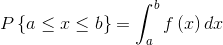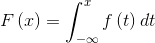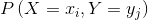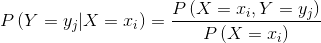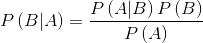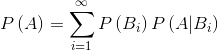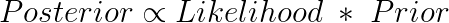前言

因为课题需要，最近在B站上看shuhuai008大佬硬核手推EM算法（Expectation Maximization），需要很多概率统计的知识，研一学的点概率论差不多全还给老师了，特此温故而知新，做做笔记，如果有什么不对的地方，还请各位大佬批评指正。

正文

概率密度函数

定义：设为一随机变量，若存在非负实函数 $f\left(x \right )$ ，是对于任意实数，有

$P\left \{ a\leq x\leq{b} \right \}=\int _{a}^{b}{f\left(x \right )dx}$

则称为连续性随机变量， $f\left(x \right )$ 成为的概率密度函数（probability density function，pdf）

分布函数： $F\left(x \right )=\int ^{x}_{-\infty}{f\left(t \right )dt}$

联合概率

Joint Probability

联合概率指的是包含多个条件且所有条件同时成立时的概率，记作 $P\left (X= x_i,Y=y_j \right )$

边缘概率

Edge probability

边缘概率是与联合概率相对的，表示取的概率，边缘概率仅与单个随机变量有关。

条件概率

Conditional Probability

表示当成立的情况下的概率，它具有如下性质：

在条件下的条件分布其实也是一种的概率分布，因此

$\sum _yP\left ( Y=y_j|X=x_i \right )=1$

联合概率、边缘概率、条件概率三者之间的关系

$P\left(Y=y_j|X=x_i \right )=\frac{P\left(X=x_i,Y=y_j \right )}{P\left(X=x_i \right )}$

后验概率

Posterior Probability

后验概率是关于随机事件或者不确定性断言的条件概率，是在相关证据或者背景给定并纳入考虑之后的条件概率。后验概率分布就是未知量作为随机变量的概率分布，并且是在基于实验或者调查所获得的信息上的条件分布。“后验”在这里意思是，考虑相关事件已经被检视并且能够得到一些信息。

条件概率可以理解为由因求果，而后验概率可以理解为由果求因

先验概率

Prior Probability

根据以往经验和分析所得到的概率，其仅仅依赖于主观上的经验估计和已有知识的推断。举个栗子，掷硬币，得到正面的概率大家都知道是0.5，这就是先验概率。

先验概率的可以用来干嘛呢，没错，可以用来计算后验概率（因为往往后验概率比先验概率难求多了！）

根据贝叶斯公式可以完成计算：

$P\left ( B|A \right )=\frac{P\left(A|B \right )P\left ( B \right )}{P\left ( A \right )}$

利用全概率公式：

$P\left ( A \right )=\sum ^{\infty}_{i=1}{P\left({B_i} \right )P\left({A|{B_i}} \right )}$

可以将贝叶斯公式展开。

其中： $P\left(B|A \right )$ 代表要计算的后验概率， $P\left(B \right )$ 代表先验概率， $P\left(A|B \right )$ 表示似然函数（Likelihood Function）， $P\left(A \right )$ 相当于一个归一化项，整个公式用一句话总结：

先验概率乘以似然函数，正比于后验概率

$\LARGE Posterior \propto Likelihood\;\ast\;Prior$