一、Optimization Objective（SVM优化目标）
在logistic回归模型中，g(z)=1/(1+e^(-z)),其函数图像如下：
在这基础上，若logistic回归只有一个样本，则Cost函数如下图所示：
（1）在y=1的情况下，只剩下Cost的左边一项，当y=0时，只剩下Cost的右边一项，其对应的图形如上图中的平滑曲线。
（2）我们在logistic曲线的基础上修改，将其修改成上图紫色曲线所示，即如下图:
SVM的代价函数：
我们通过最小化目标函数能够得到对应的参数值C
支持向量机中h(x)如下：
二、Large Margin Intuition（最大间隔的直观感知）
在上面的内容中讲到SVM的目标函数是：
若C是一个非常大的数，假设C=100,0000，则我们希望找到一个能使C后面的求和数
为0的解，这样会使得目标函数最小化，在这种情况下，目标函数变成：
SVM决策边界：线性划分
这里引入margin的概念，如下图：
SVM便是努力将正样本和负样本用最大间距分开。
存在离群点的线性可分边界
上图中A、B、C、D都是异常数据。
在不考虑异常数据的情况下，若C非常大，原来的边界应该是黑色的线，但是在加入
了异常点A之后，边界变成紫色的线，因为一个异常点就改变了划分边界，这是不明智的。
因此，若C不是非常大，即使一些异常数据，如A、B、C、D等，SVM也能够把不同的
类正确区分开（支持向量机这时候可以忽略一些异常数据，得到更好的决策边界），
甚至不是线性可分的情况下，SVM也可以得到好的结果。
三、Mathematics Bebind Large Margin Classification（最大间隔分类背后的数学原理）
本部分内容主要讲最大间距分类器的数学原理。
首先了解内积的概念：
其中p是可正可负。
如下图：
SVM决策边界：
下图说明为何SVM会选择具有最大间隔的超平面（决策边界）：
（1）先看左图，这是一个反面示例，绿色的线表示决策边界，这不是一个好的决策边界，
不是好的决策边界原因：
正例情况下，即当
时，
，从图中可以看到，p^(1)较小，因此
若需要满足不等式，||θ||需要非常大。
负例情况下，即当
时，
，从图中可以看到，p^(2)较小，因此
若需要满足不等式，||θ||需要非常大。
但是，最小化目标函数
需要||θ||越小越好，因此出现矛盾，因此这个绿色
决策边界不是一个很好的
决策边界。
（2）再看右图，右图中绿色的线表示决策边界，这是一个很好的决策边界的原因：
当
时，
，从图中可以看到，p^(1)(红色)比（1）中的大很多，
因此满足不等式，||θ||可以比之前变小很多。
当
时，
，从图中可以看到，p^(2)(紫色)比（1）中的大很多，
因此满足不等式，||θ||可以比之前变小很多。
因此，图2绿色的决策边界线，能保证||θ||取值较小，满足我们的要求。
因为SVM试图极大化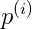
附上一道练习题：
解答：
在本图中，X表示正样本，O表示负样本。
在本题中，最优决策边界肯定是y轴，又θ是决策边界的法向量，因此θ向量和x轴重合（x轴的正方向即为θ向量的正方向），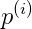
||θ||
应该满足
因此只需要考虑支持向量，所谓支持向量表示离超平面最近的那个样本，
这里考虑的是x=2（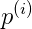
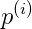
（1）考虑正样本，x=2（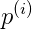
（2）考虑负样本，x=-2（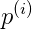
因此，||θ||≥1/2，取||θ||=1/2；
（可以验证一下，x=3（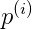
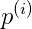
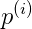
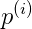
注：
如果根据正负样本，一个求出||θ||≥2，一个求出||θ||≥3，则为了让所有样本满足不等式条件，需要取两者的交集，即||θ||≥3。