1.硬币找零
如果我们有面值为 1 元、3 元和 5 元的硬币若干枚,如何用最少的硬币凑够 11 元?
首先我们思考一个问题,如何用最少的硬币凑够 i 元(i<11)?为什么要这么问呢? 两个原因:1.当我们遇到一个大问题时,总是习惯把问题的规模变小,这样便于分析讨论。 2.这个规模变小后的问题和原来的问题是同质的,除了规模变小,其它的都是一样的, 本质上它还是同一个问题(规模变小后的问题其实是原问题的子问题)。
好了,让我们从最小的 i 开始吧。当 i=0,即我们需要多少个硬币来凑够 0 元。 由于 1,3,5 都大于 0,即没有比 0 小的币值,因此凑够 0 元我们最少需要 0 个硬币。 (这个分析很傻是不是?别着急,这个思路有利于我们理清动态规划究竟在做些什么。) 这时候我们发现用一个标记来表示这句“凑够 0 元我们最少需要 0 个硬币。”会比较方便, 如果一直用纯文字来表述,不出一会儿你就会觉得很绕了。那么, 我们用 d(i)=j 来表示凑够 i 元最少需要 j 个硬币。于是我们已经得到了 d(0)=0, 表示凑够 0 元最小需要 0 个硬币。当 i=1 时,只有面值为 1 元的硬币可用, 因此我们拿起一个面值为 1 的硬币,接下来只需要凑够 0 元即可,而这个是已经知道答案的, 即 d(0)=0。所以,d(1)=d(1-1)+1=d(0)+1=0+1=1。当 i=2 时, 仍然只有面值为 1 的硬币可用,于是我拿起一个面值为 1 的硬币, 接下来我只需要再凑够 2-1=1 元即可(记得要用最小的硬币数量),而这个答案也已经知道了。 所以 d(2)=d(2-1)+1=d(1)+1=1+1=2。一直到这里,你都可能会觉得,好无聊, 感觉像做小学生的题目似的。因为我们一直都只能操作面值为 1 的硬币!耐心点, 让我们看看 i=3 时的情况。当 i=3 时,我们能用的硬币就有两种了:1 元的和 3 元的( 5 元的仍然没用,因为你需要凑的数目是 3 元!5 元太多了亲)。 既然能用的硬币有两种,我就有两种方案。如果我拿了一个 1 元的硬币,我的目标就变为了: 凑够 3-1=2 元需要的最少硬币数量。即 d(3)=d(3-1)+1=d(2)+1=2+1=3。 这个方案说的是,我拿 3 个 1 元的硬币;第二种方案是我拿起一个 3 元的硬币, 我的目标就变成:凑够 3-3=0 元需要的最少硬币数量。即 d(3)=d(3-3)+1=d(0)+1=0+1=1. 这个方案说的是,我拿 1 个 3 元的硬币。好了,这两种方案哪种更优呢? 记得我们可是要用最少的硬币数量来凑够 3 元的。所以, 选择 d(3)=1,怎么来的呢?具体是这样得到的:d(3)=min{d(3-1)+1, d(3-3)+1}。
OK,码了这么多字讲具体的东西,让我们来点抽象的。从以上的文字中, 我们要抽出动态规划里非常重要的两个概念:状态和状态转移方程。
上文中 d(i)表示凑够 i 元需要的最少硬币数量,我们将它定义为该问题的”状态”, 这个状态是怎么找出来的呢?一般来说,我们可以根据子问题定义状态。你找到子问题,状态也就浮出水面了。 最终我们要求解的问题,可以用这个状态来表示:d(11),即凑够 11 元最少需要多少个硬币。 那状态转移方程是什么呢?既然我们用 d(i)表示状态,那么状态转移方程自然包含 d(i), 上文中包含状态 d(i)的方程是:d(3)=min{d(3-1)+1, d(3-3)+1}。没错, 它就是状态转移方程,描述状态之间是如何转移的。当然,我们要对它抽象一下,
d(i)=min{ d(i-vj)+1 },其中 i-vj >=0,vj表示第 j 个硬币的面值;
有了状态和状态转移方程,这个问题基本上也就解决了。
def coins_solve(n):
minarray = [x for x in range(n+1)]
coins = [1, 3, 5]
for i in range(n+1):
for j in coins:
# min {d(i - vj) + 1}
if j <= i and minarray[i-j] + 1 < minarray[i]:
minarray[i] = minarray[i - j] + 1
print minarray
print "the result is: ", minarray[-1]
coins_solve(11)
2.最长非降子序列(LIS:longest increasing subsequence)
一个序列有 N 个数:A[1],A[2],…,A[N],求出最长非降子序列的长度。
正如上面我们讲的,面对这样一个问题,我们首先要定义一个“状态”来代表它的子问题, 并且找到它的解。注意,大部分情况下,某个状态只与它前面出现的状态有关, 而独立于后面的状态。
让我们沿用“入门”一节里那道简单题的思路来一步步找到“状态”和“状态转移方程”。 假如我们考虑求 A[1],A[2],…,A[i]的最长非降子序列的长度,其中 i<N, 那么上面的问题变成了原问题的一个子问题(问题规模变小了,你可以让 i=1,2,3 等来分析) 然后我们定义 d(i),表示前 i 个数中以 A[i]结尾的最长非降子序列的长度。OK, 对照“入门”中的简单题,你应该可以估计到这个 d(i)就是我们要找的状态。 如果我们把 d(1)到 d(N)都计算出来,那么最终我们要找的答案就是这里面最大的那个。 状态找到了,下一步找出状态转移方程。
根据上面找到的状态,我们可以得到:(下文的最长非降子序列都用 LIS 表示)
前 1 个数的 LIS 长度 d(1)=1(序列:5)
前 2 个数的 LIS 长度 d(2)=1(序列:3;3 前面没有比 3 小的)
前 3 个数的 LIS 长度 d(3)=2(序列:3,4;4 前面有个比它小的 3,所以 d(3)=d(2)+1)
前 4 个数的 LIS 长度 d(4)=3(序列:3,4,8;8 前面比它小的有 3 个数,所以 d(4)=max{d(1),d(2),d(3)}+1=3)

OK,分析到这,我觉得状态转移方程已经很明显了,如果我们已经求出了 d(1)到 d(i-1), 那么 d(i)可以用下面的状态转移方程得到:
d(i) = max{1, d(j)+1},其中 j<i,A[j]<=A[i]
用大白话解释就是,想要求 d(i),就把 i 前面的各个子序列中, 最后一个数不大于 A[i]的序列长度加 1,然后取出最大的长度即为 d(i)。 当然了,有可能 i 前面的各个子序列中最后一个数都大于 A[i],那么 d(i)=1, 即它自身成为一个长度为 1 的子序列。
def LIS(rawlist):
d = [1 for _ in range(len(rawlist))]
result = 1
for i in range(len(rawlist)):
for j in range(i):
if rawlist[j] <= rawlist[i]:
d[i] = max(d[i], d[j] + 1)
result = max(result, d[i])
print result
rawlist = [5, 3, 4, 8, 6, 7]
LIS(rawlist)
3.背包问题
我们需要选择n个元素中的若干个来形成最优解,假定为k个。那么对于这k个元素a1, a2, …ak来说,它们组成的物品组合必然满足总重量<=背包重量限制,而且它们的价值必然是最大的。因为它们是我们假定的最优选择嘛,肯定价值应该是最大的。假定ak是我们按照前面顺序放入的最后一个物品。它的重量为wk,它的价值为vk。既然我们前面选择的这k个元素构成了最优选择,如果我们把这个ak物品拿走,对应于k-1个物品来说,它们所涵盖的重量范围为0-(W-wk)。假定W为背包允许承重的量。假定最终的价值是V,剩下的物品所构成的价值为V-vk。这剩下的k-1个元素是不是构成了一个这种W-wk的最优解呢?
我们可以用反证法来推导。假定拿走ak这个物品后,剩下的这些物品没有构成W-wk重量范围的最佳价值选择。那么我们肯定有另外k-1个元素,他们在W-wk重量范围内构成的价值更大。如果这样的话,我们用这k-1个物品再加上第k个,他们构成的最终W重量范围内的价值就是最优的。这岂不是和我们前面假设的k个元素构成最佳矛盾了吗?所以我们可以肯定,在这k个元素里拿掉最后那个元素,前面剩下的元素依然构成一个最佳解。
现在我们经过前面的推理已经得到了一个基本的递推关系,就是一个最优解的子解集也是最优的。可是,我们该怎么来求得这个最优解呢?我们这样来看。假定我们定义一个函数c[i, w]表示到第i个元素为止,在限制总重量为w的情况下我们所能选择到的最优解。那么这个最优解要么包含有i这个物品,要么不包含,肯定是这两种情况中的一种。如果我们选择了第i个物品,那么实际上这个最优解是c[i - 1, w-wi] + vi。而如果我们没有选择第i个物品,这个最优解是c[i-1, w]。这样,实际上对于到底要不要取第i个物品,我们只要比较这两种情况,哪个的结果值更大不就是最优的么?
在前面讨论的关系里,还有一个情况我们需要考虑的就是,我们这个最优解是基于选择物品i时总重量还是在w范围内的,如果超出了呢?我们肯定不能选择它,这就和c[i-1, w]一样。
这里有一点值得注意,这里的wi指的是第i个物品的重量,而不是到第i个物品时的总重量。
另外,对于初始的情况呢?很明显c[0, w]里不管w是多少,肯定为0。因为它表示我们一个物品都不选择的情况。c[i, 0]也一样,当我们总重量限制为0时,肯定价值为0。
这样,基于我们前面讨论的这3个部分,我们可以得到一个如下的递推公式:
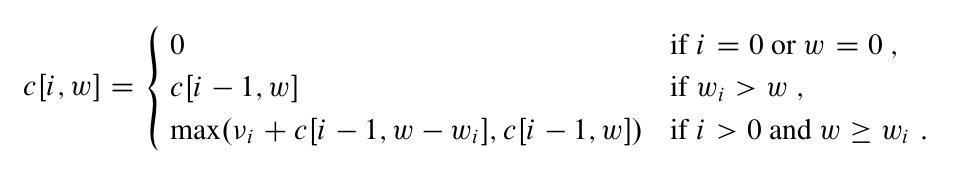
有了这个关系,我们可以更进一步的来考虑代码实现了。我们有这么一个递归的关系,其中,后面的函数结果其实是依赖于前面的结果的。我们只要按照前面求出来最基础的最优条件,然后往后面一步步递推,就可以找到结果了。
我们再来考虑一下具体实现的细节。这一组物品分别有价值和重量,我们可以定义两个数组int[] v, int[] w。v[i]表示第i个物品的价值,w[i]表示第i个物品的重量。为了表示c[i, w],我们可以使用一个int[i][w]的矩阵。其中i的最大值为物品的数量,而w表示最大的重量限制。按照前面的递推关系,c[i][0]和c[0][w]都是0。而我们所要求的最终结果是c[n][w]。所以我们实际中创建的矩阵是(n + 1) x (w + 1)的规格。
# n:物品件数;c:最大承重为c的背包;w:各个物品的重量;p:各个物品的价值
# 第一步建立最大价值矩阵(横坐标表示[0,c]整数背包承重):(n+1)*(c+1)
# 技巧:python 生成二维数组(数组)通常先生成列再生成行
def bag(n,c,w,p):
res=[[-1 for j in range(c+1)]for i in range(n+1)]
for j in range(c+1):
# 第0行全部赋值为0,物品编号从1开始.为了下面赋值方便
res[0][j]=0
for i in range(1, n+1):
for j in range(1, c+1):
res[i][j]=res[i-1][j]
# 生成了n*c有效矩阵,以下公式w[i-1],p[i-1]代表从第一个元素w[0],p[0]开始取。
if(j >= w[i-1]) and res[i-1][j-w[i-1]]+p[i-1]>res[i][j]:
res[i][j] = res[i-1][j-w[i-1]]+p[i-1]
return res
# 以下代码功能:标记出有放入背包的物品
# 反过来标记,在相同价值情况下,后一件物品比前一件物品的最大价值大,则表示物品i#有被加入到背包,x数组设置为True。设初始为j=c。
def show(n, c, w, res):
print '最大价值为:',res[n][c]
x=[False for i in range(n)]
j=c
for i in range(1,n+1):
if res[i][j]>res[i-1][j]:
x[i-1]=True
j-=w[i-1]
print '选择的物品为:'
for i in range(n):
if x[i]:
print '第',i,'个,'
print''
if __name__=='__main__':
n=5
c=10
w=[2,2,6,5,4]
p=[6,3,5,4,6]
res=bag(n,c,w,p)
show(n,c,w,res)
最后的结果为:
最大价值为: 15
选择的物品为:
第 0 个,
第 1 个,
第 4 个,
参考文献:
1.https://www.deeplearn.me/216.html
2.https://www.jianshu.com/p/25f4a183ede5