1、基本形式

对含有d个特征的数据x，线性模型试图学得一个通过特征的线性组合来进行预测的函数：

f(x) = w1x1 + w2x2 + .......wdxd + b

一般用向量形式写成：

f(x) = w^T x + b

线性模型得以对每个不同的特征进行权重考量，它形式简单，易于建模，虽然对于大多数复杂问题来说线性模型效果不好，但它却是很多复杂模型的基础；

2、线性回归

首先考虑最简单的情况，样本只有一个属性，这时是单个特征的线性回归。

2.1 单元线性回归

第一步：特征值连续化

因为建模需要运用数字进行计算，对于特征值是数字的可以直接使用，然而，对于特征值不是数字的则无法进行建模运算（例如形容一个人的特征为高矮胖瘦时，不对其进行数字化则无法建模运算），此时需要将其转化后方可进行建模。

对于特征值的离散属性，如果其属性有“序”，可通过连续化将其转化为连续值；如身高属性的取值“高”、“矮”可转化为{1.0，0.0}，“高”、“中”、“低”可转化为{1.0，0.5，0.0}；如果属性值之间不存在“序”关系，通常会根据属性值的个数（如k个）进行k维向量化，(0,0,1)，(0,1,0)，(1,0,0)。

第二步：确定回归模型

线性回归试图学得：

扫描二维码关注公众号，回复： 4579914 查看本文章

$f(x_{i}) = wx_{i} + b,$ 使得 $f(x_{i}) \simeq y_{i} .$

显然，模型的关键在于得到一个最好的w和b使得f(x) 尽可能的减少与yi之间的误差，问题化简为求(yi-f(x))^2 的最小值问题：

$E_{(w,b)} = \sum_{i=1}^{m} (y_{i} -wx_{i} -b)^{2} .$ 的最小值。

由函数的凹凸性可知，对于凸函数，当其倒数为0时能取得最小值，故对w、b进行求导：

$\frac{\partial E_{(w,b)}}{\partial w} = 2(w\sum_{i=1}^{m}x_{i}^{2} - \sum_{i=1}^{m}(y_{i}-b)x_{i})$

$\frac{\partial E_{(w,b)}}{\partial b} = 2(mb - \sum_{i=1}^{m}(y_{i}-wx_{i}))$

令其为0即可求得w、b的值：

$w = \frac{\sum_{i=1}^{m}y_{i}(x_{i} - \bar{x})}{\sum_{i=1}^{m}x_{i}^{2} - \frac{1}{m}(\sum_{i=1}^{m}x_{i})^{2}} ,$ 其中 $\bar{x} = \frac{1}{m}\sum_{i=1}^{m}x_{i}$

$b = \frac{1}{m}\sum_{i=1}^{m}(y_{i} - wx_{i}) ,$

推导过程比较简单，这里就不演示了。

2.2 多元线性回归

上面讨论的是样本只有一个属性的情况，扩展到多维属性上时，比如一个数据集里面的样本由d个属性描述时，我们试图让模型学得如下回归函数：

$f(x_{i}) = w^{T}x_{i} + b$ 使得 $f(x_{i}) \simeq y_{i} .$

同样用最小二乘法来对w和b进行估计，由于此时扩展到d维属性，这里用矩阵的形式来便于讨论。

w、b用向量的形式表示 $\hat{w} = (w;b)$ ;

将数据集D表示为一个 m行(d+1)列大小的矩阵

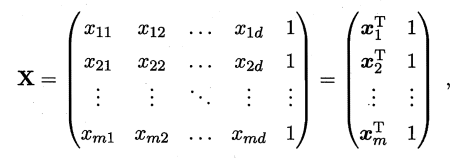说明：m行表示数据集有m个，d+1列表示前d个特征值和修正量b的对应值。

将实际值y也写成向量的形式： $y = (y_{1};y_{2};y_{3};....;y_{m})$ ;

求误差的最小值：

$E\hat{w} = (y-X\hat{w})^{T}(y-X\hat{w})$

对 $\hat{w}$ 求导得：

$\frac{\partial E_{\hat{w}}}{\partial \hat{w}} = 2X^{T}(X\hat{w}-y)$

令上式为0即可得到最优解：

此时要注意，当 $X^{T}X$ 为满秩矩阵或正定矩阵时，解唯一： $\hat{w} = (X^{T}X)^{-1}X^{T}y ,$ 当 $X^{T}X$ 不是满秩矩阵时（实际情况往往是这样），此时解不唯一，会得到多组满足条件的最优解，至于选哪个作为输出，将由学习算法的归纳偏好（笔记一中提到的）决定，通常会引入正则化。

线性模型虽然简单，但却有多种形式的变形，比如 $lny = w^{T}x +b$ 虽然看上去还是线性模型，但实际上它已经是对数函数的一种映射，这就是”对数线性回归“。

更一般地，对于单调可微函数g(·)，令 $g(y) = w^{T}x +b$ , 则

$y = g^{-1}(w^{T}x +b)$ "广义线性模型”

2.3 对数几率回归

说是回归，其实解决的是分类问题；因为使用了阶跃函数，使得对不同的分类x总有唯一的y值对应，比如x > 0时，y取值为1 ，x < 0时，y取值为0。之所以还是将其称为回归函数，主要是它还是使用了广义的线性模型。但是，普通的阶跃函数是不连续的，不满足广义线性模型中g(·)单调可微的条件，因此，我们希望找到一个“替代函数”近似阶跃函数并且单调可微，而对数几率函数正好满足要求：

$y = \frac{1}{1 + e^{-z}}$

将其作为 $g^{-}(\cdot )$ 带入广义线性模型中得到：

$y = \frac{1}{1 + e^{-(w^{T}x+b)}}$

按照广义线性模型的样式，上式可转化为：(转化过程自行推导，就是简单的列式转换)

$ln\frac{y}{1-y} = w^{T}x+b$

从上式可以看出，实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率。

此时对于w、和b的求解可以先通过最大似然法来估计，然后利用梯度下降法或牛顿法来求其最优解。

2.4 线性判别分析

线性判别分析（LDA）是一种经典的处理二分类问题的方法，也可以称为“Fisher判别分析”，但是严格说来，LDA假设了各类样本的协方差矩阵相同且满秩，因此，两者还是有一些区别的。

主要思想：通过给定的训练数据来找到一条直线使得训练数据中不同分类里面的点投影到该直线上时尽可能的接近，而不属于该类的点在直线上的投影尽可能的远离；最后，通过训练好的该模型，只需给定一个点就能判断它属于哪一类。

LDA可用于二分类也可用于多分类，由于使用的是投影的方式，从而可以降低样本的维数，而且投影过程中使用了类别信息，因此LDA也常被视为一种经典的监督降维技术。

2.5 多分类学习

有些二分类学习方法可以直接推广到多分类，这里我们主要是使用二分类学习器来解决多分类问题。
考虑N个类别C1,C2,…,CN这里我们将N分类问题拆解若干个二分类问题进行求解。

一对一分类（One vs One, OvO）：将N个类别两两配对，产生N(N−1)/2个分类任务，测试时将新样本输入给所有分类器，选择预测结果最多的类别作为最终分类结果。
一对其余分类（One vs Rest, OvR）：每次将一个类别的样本作为正类，其余所有类别的样本作为负类，构建N个分类器。同样将测试样本输入到所有分类器中，若只有一个分类器预测为正类，则对应的类别作为最终分类结果；若有多个分类器预测为正类，通常考虑各个分类器的预测置信度，选择置信度最大的类别标记作为分类结果。
多分类样本数分类器个数
OvO 两类样本 N(N−1)/2
OvR 所有样本 N
OvO需要训练N(N−1)/2分类器，而OvR只需训练N个分类器，通常其存储开销和测试时间开销更小；但OvR的每个分类器需要使用全部样本数据，在类别很多时，训练时间开销通常更大。

2.6 类别不平衡问题

类别不平衡：分类任务中存在的不同类别（对于二分类就是正负类别）训练样本数量差别很大的情况。在这里，我们假设对于二分类问题，正样本数很少，负样本数很多（比如广告点击率），主要有以下三种处理办法：

欠采样：去除一些训练集中的负样本使得正负样本数相当
过采样：增加一些正样本数使得正负样本数相当
阈值移动：基于原始训练集进行训练，在用分类器判别时修改判决阈值

欠采样：训练集样本数变少，训练时间减少，可能会出现欠拟合。代表性算法EasyEnsemble利用集成学习算法，将负样本划分为若干个集合供不同的学习器使用。
过采样：增加了很多正样本，训练集变大，可能会出现过拟合。代表性算法SMOTE通过对正样本进行插值来产生额外的正样本。
阈值移动：在假设“训练集是真实样本总体的无偏估计”的前提下，我们基于训练集中正负样本的数目对判别器进行缩放。原来的判别阈值为0.5，即
若 $\frac{y}{1-y} > 1$ , 则预测为正类
现在在训练集中假设正样本数为 $m^{+}$ ,负样本数为 $m^{-}$ ，则正样本对于负样本的观测几率为 $\frac{m^{+}}{m^{-}}$ ，在上述假设下，观测几率代表了真实几率。所以只要分类器的预测几率高于观测几率就应该判定为正类，即
若 $\frac{y}{1-y} > \frac{m^{+}}{m^{-}}$ , 则预测为正类
我们对于分类器的判别阈值进行缩放，令
$\frac{y'}{1-y'} = \frac{y}{1-y} \times \frac{m^{-}}{m^{+}}$
即可。

机器学习（西瓜书）学习笔记（二）---------线性模型