本文主要记录《机器学习》第三章-线性模型的部分内容。
线性模型基本形式
线性模型的向量形式:
f ( x ) = w T x + b f(\bm x) = \bm w^T \bm x + b f(x)=wTx+b线性模型形式简单、建模也容易,权重向量 w \bm w w直观表达了输入样本 x \bm x x各个特征维度在预测中的重要性,从而具有很好的可解释性(comprehensibility),这是线性模型的优点。
另外,线性模型蕴涵机器学习的一些重要思想,许多功能更为强大的非线性模型(nolinear model)是在线性模型的基础上引入 层级结构 或 高级映射 而得。
线性回归
线性模型的经典任务之一就是回归任务,所谓“线性回归”(linear regression)任务,就是试图训练一个线性模型,以尽可能准确地对新样本预测其输出标签。
一般的情形是:
对于给定的数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x m , y m ) } D=\{(\bm x_1,y_1), (\bm x_2,y_2), \cdots, (\bm x_m,y_m)\} D={
(x1,y1),(x2,y2),⋯,(xm,ym)},其中 x i = ( x i 1 ; x i 2 ; ⋯ ; x i d ) , y i ∈ R . \bm x_i=(x_{i1}; x_{i2}; \cdots; x_{id}), y_i \in \mathbb R. xi=(xi1;xi2;⋯;xid),yi∈R. 线性回归的任务是试图学得
f ( x ) = w T x + b , 使 得 f ( x i ) ≃ y i f(\bm x) = \bm w^T \bm x + b,使得f(\bm x_i) \simeq y_i f(x)=wTx+b,使得f(xi)≃yi这称为“多元线性回归”(multivariate linear ergression).
学习的任务就是确定权值向量 w \bm w w 以及偏置量 b b b,为了便于讨论,记 w ^ = ( w ; b ) \hat {\bm w} = (\bm w; b) w^=(w;b), y = ( y 1 ; y 2 ; ⋯ ; y m ) \bm y = (y_1;y_2;\cdots;y_m) y=(y1;y2;⋯;ym),
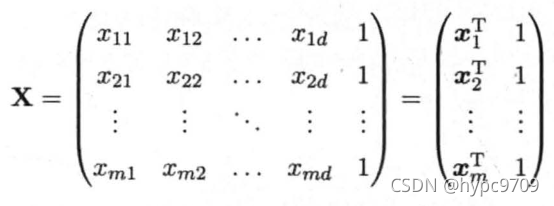
那要如何确定 w ^ \hat {\bm w} w^呢?首先需要有一个衡量模型预测值 f ( x i ) f(\bm x_i) f(xi)与实际值 y y y之间差别的指标,常用的一个指标就是均方误差:
E w ^ = ( y − X w ^ ) T ( y − X w ^ ) E_{\hat {\bm w}} = (\bm y - \bm X\hat {\bm w})^T(\bm y - \bm X\hat {\bm w}) Ew^=(y−Xw^)T(y−Xw^) 让均方误差最小化,可得到 w ^ \hat {\bm w} w^,即 w ^ ∗ = arg min w ^ ( y − X w ^ ) T ( y − X w ^ ) \hat {\bm w}^* = \arg \min_{\hat {\bm w}} (\bm y - \bm X\hat {\bm w})^T(\bm y - \bm X\hat {\bm w}) w^∗=argw^min(y−Xw^)T(y−Xw^)进而得到多元线性回归模型。
对数几率回归
线性模型的应用除了回归任务外,还有分类任务。
当线性模型应用于分类任务时,只需要找到一个单调可微函数将分类任务的真实标记 y y y 与回归模型的预测值联系起来。
以二分类任务为例,输出标记 y ∈ { 0 , 1 } y\in\{0,1\} y∈{ 0,1},而线性回归模型产生的预测值 z = w T x + b z = \bm w^T \bm x+ b z=wTx+b是实数值,为了将两者联系起来,需要找到一个单调可微函数,常用的是对数几率函数(logistic function): y = 1 1 + e − z y = \frac{1}{1 + e^{-z}} y=1+e−z1这个函数将 z z z值转化为一个接近0或1的值,将 z = w T x + b z = \bm w^T \bm x+ b z=wTx+b代入得到 y = 1 1 + e − ( w T x + b ) ⇒ ln y 1 − y = w T x + b y = \frac{1}{1 + e^{-( \bm w^T \bm x+ b)}} \quad \Rightarrow \quad \ln\frac{y}{1-y} = \bm w^T \bm x+ b y=1+e−(wTx+b)1⇒ln1−yy=wTx+b可以看出,这样的模型实际上是在用线性回归模型的预测结果 w T x + b \bm w^T \bm x+ b wTx+b 去逼近真实标记 y y y的对数几率 ln y 1 − y \ln\frac{y}{1-y} ln1−yy,因此被称为“对数几率回归”(logistic regression)模型。虽然名字是“回归”,但实际上是一种分类学习方法。
上述方法的优点:
- 直接对分类可能性建模,无须事先假设数据分布
- 不仅能预测出“类别” ,而且可以得到近似概率预测,在一些需要利用概率辅助决策的任务中将会很有用
- 对数几率函数是任意阶可导的凸函数,有很好的数学性质,现有的很多数值优化算法可直接用于求取最优解
确定上述模型中的 w 和 b \bm w和b w和b,可通过“极大似然法”来估计。
线性判别分析(LDA)
线性判别分析(Linear Discriminant Analysis, LDA)的基本思想如下:
给定训练样本集,设法将所有样本投影到一条直线,使得属于同一类的样本在该直线上的投影点尽可能接近、而属于不同类的样本的投影点尽可能远离;训练完模型,在应用到新样本时,即对新样本进行分类时,将其投影到同样的直线,根据新样本的投影点到各类样本中心点的距离来确定其类别,距离哪一类近,就属于哪一类。