【NOIP2018提高组D2T2】填数游戏

Description

小D特别喜欢玩游戏。这一天，他在玩一款填数游戏。
这个填数游戏的棋盘是一个n*m的矩形表格。玩家需要在表格的每个格子中填入一个数字（数字0或者数字1），填数时需要满足一些限制。
下面我们来具体描述这些限制。
为了方便描述，我们先给出一些定义：
我们用每个格子的行列坐标来表示一个格子，即（行坐标，列坐标）。（注意：行列坐标均从0开始编号）
合法路径P：一条路径是合法的当且仅当：
1.这条路径从矩形表格的左上角的格子(0,0) 出发，到矩形的右下角格子(n-1,m-1) 结束；
2.在这条路径中，每次只能从当前的格子移动到右边与它相邻的格子，或者从当前格子移动到下面与它相邻的格子。
例如：在下面这个矩形中，只有两条路径是合法的，它们分别是P1：(0,0)->(0,1)->(1,1) 和 P2：(0,0)->(1,0)->(1,1) 。
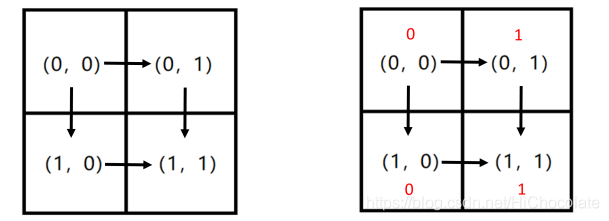
在这里插入图片描述

对于一条合法的路径P，我们可以用一个字符串w§ 来表示，该字符串的长度为n+m-2，其中只包含字符“R”或者字符“D”，第i个字符记录了路径P中第i步的移动方法，“R”表示移动到当前格子右边与它相邻的格子，“D”表示移动到当前格子下面与它相邻的格子。例如，上图中对于路径P1 ，有w(P1)=“RD” ；而对于另一条路径p2 ，有w(P2)=“DR” 。
同时，将每条合法路径P经过的每个格子上填入的数字依次连接后，会得到一个长度为n+m-1的01字符串，记为s§ 。例如，如果我们在格子(0,0) 和(1,0) 上填入数字0，在格子(0,1) 和(1.1) 上填入数字1（见上图红色数字）。那么对于路径P1，我们可以得到s(P1)=“011” ,对于路径P2 ，有s(P2)=“001” 。
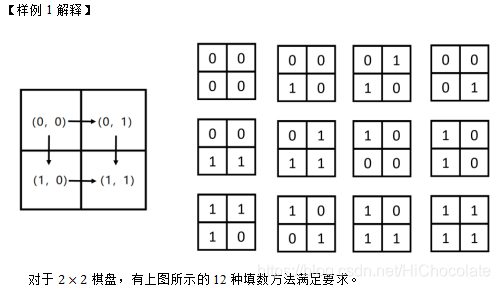
游戏要求小D找到一种填数字0、1的方法，使得对于两条路径P1 ，P2 ，如果w(P1)>=w(P2) ，那么必须s(P1)<=s(P2) 。我们说字符串a比字符串b小，当且仅当字符串a的字典序小于字符串b的字典序，字典序的定义详见第一题。但是仅仅是找一种方法无法满足小D的好奇心，小D更想知道这个游戏有多少种玩法，也就是说，有多少种填数字的方法满足游戏的要求？
小D能力有限，希望你帮助他解决这个问题，即有多少种填0、1的方法能满足题目要求。由于答案可能很大，你需要输出答案对10^9+7 取模的结果。

Input

输入文件名为game. in。
输入文件共一行，包含两个正整数n、m，由一个空格分隔，表示矩形的大小。其中n 表示矩形表格的行数，m表示矩形表格的列数。

Output

输出文件名为game.out。
输出共一行，包含一个正整数，表示有多少种填0、1的方法能满足游戏的要求。注意：输出答案对10^9+7取模的结果。

Sample Input

输入1：
2 2

输入2：
3 3

输入3：
5 5

Sample Output

输出1：
12

输出2：
112

输出3：
7136

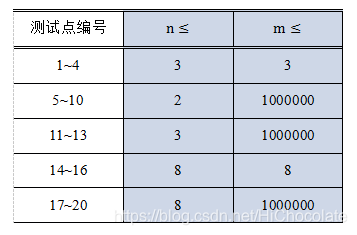
Data Constraint

在这里插入图片描述

Hint

在这里插入图片描述

题解

首先题意有点不清不楚的，其实它是对于任意两条路径都要满足：
P1 ，P2 ，如果w(P1)>=w(P2) ，那么必须s(P1)<=s(P2) 。
然而题目原来的意思中没有“任意”二字，搞得我理解非常困难。

20%
我们可以发现，这档部分分可以直接 $O(2^{nm})$ 时间暴力搞。
65%
既然我们已经打了暴力了，我们何不直接找规律？
n=2,3的规律很好找。不说了。
假的100%
既然我们也有了暴力，那么跑上2个小时不就可以找到n<=8的规律了吗？
打个表很方便的。不说了。
题解的100%
我们发现，n<=8。那么就有一个简单明了的思路——状压dp。
我们又观察得，在构造一个新的方阵时，是一条斜斜的线的状态影响到下面的状态。
那么我们就可以从中入手。

当然，dp出来的状态很多都是无用的，所以可以相对应地优化。
细节很多，具体~~我也不会~~自己思考。
更厉害的100%
这种方法其实是可以做到log级别复杂度的，所以说，题目范围可以变成这样：
1<=n,m<=10^18
可能还可以更多。

废话不多说：
我们可以依据题解100分的方法，发现，每次也是一条斜斜的线对之后的答案影响。
那么，我们就看看可否快速求出答案。
开始分类讨论：
为了方便，我们设题目给定的0 ~ n-1看做是1 ~ n

首先我们考虑n=m的情况。
- 当：（1,2）和（2,1）两个格子填的是相同的数字时
  - 我们可以发现在（2,2）到（n,n）这一个矩阵内的每一个斜线上数字都要相同，否则不成立。我们说这个矩阵是被“控制”的。
  - 这里红色线的部分是控制的，都是要填相等的，但是白色的格子是不受控制的。
  - 于是我们就可以发现，对于红蓝绿三色的斜线：
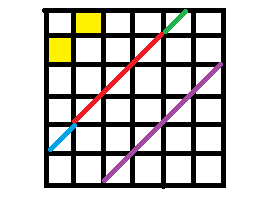
  - 就有4种填法。（三种颜色看做三个点，下面的点要比上面的点大或相等）
  - 而没有的话就像紫色只有2种填法。
  - 一共加起来就是 $2*2*(4*(n-2))*2^{n-1}$
- 当：（1,2）和（2,1）不相等时且（3,1）（2,2）（1,3）相等时
  - 我们发现，第4条斜线是四个独立的点，那么就可以有5种填法。
  - 然而后面的红色斜线是被控制的，所以说和上面的一样有4种填法。
  - 而紫色的同上。
  - 一共加起来就是 $2*1*2*5*(4*(n-4))*2^{n-1}$
- 当：（1,2）和（2,1）不相等时且（3,1）（2,2）相等时
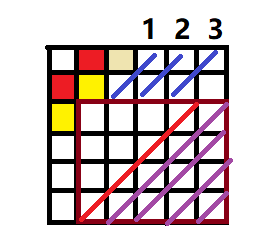
  - 那么我们发现上面有两行是不受控制的。
  - 我们就设f[i]表示第i条不受控制的对角线之前有过一条对角线是相等的填法。
  - 1、当i-1前面有的话，那么i就是被影响的，就相当于分成3块独立的数，有4种填法： $f[i-1]*4$
  - 2、当i-1前面没有的话，那么i-1就是有的，分成3块。然而i没有被影响到，所以依旧分成4块。填法： $4*5$
  - 那么 $f[i]=f[i-1] * 4 + 4 * 5$ 这样转移。
  - 意义： $(i-1以前有过匹配成功的方案) * (i的方案)+(i-1这匹配成功) * (i的方案)$
  - 这样我们可以使用f[n-3]来快速计算红线的答案
  - 一共加起来就是 $2*1*1*(f[n-3]*2+3*5)*2^{n-2}$
  - 意义： $第一个斜*第二个斜*第三个斜*((n-3个对角线前有相等的，那么红线就有2种填法)+(n-3前不相等，那么红线有3种填法，n-3这斜线有5种填法))*紫色线$
- 然而我们发现，（2,2）（1,3）相等时同上，那么我们就对n=m讨论完了。
- 答案即为： $2*2*(4*(n-2))*2^{n-1}+2*1*2*5*(4*(n-4))*2^{n-1}+2*(2*1*1*(f[n-3]*2+3*5)*2^{n-2})$
我们再考虑n<m的情况
我们可以发现，其实n<m时，只需要弄好（3,1）（2,2）相等和（2,2）（1,3）相等时就好了。
- 当：（2,2）（1,3）相等时
  - 在这种情况，我们依旧从f[n-3]下手。
  - 分类讨论：
  - 1、当f[n-3]前有匹配好的，那么可以发现紫色以及之后的斜线都被控制，但是这个多出来的粉色的斜线，我们也可以发现这个情况下粉色的斜线只有上面n+1号格子是不被控制的，那么答案就是： $f[n-3]*3(粉色线)*2^{n-1}$
  - 2、若是f[n-3]前没有匹配好，那么n-3这一对角线无论相等或不等都无法影响后面答案。答案即为： $5*4(粉色线)*2^{n-1}$
- 当：（3,1）（2,2）相等时
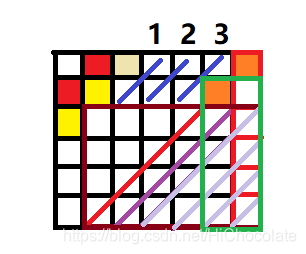
  - 我们接着讨论：
  - 1、当f[n-3]前有匹配的话，那么红色线那一斜线只有3种填法。那么答案就是： $2*1*1*f[n-3]*3*2^{n-1}$
  - 意义： $第一个斜*第二个斜*第三个斜*(n-3个对角线前有相等的，那么红线就有3种填法)*紫色线后的方案$
  - 2、当f[n-3]前没有的话，当f[n-3]这里相等，则f[n-3]所在斜线填法有4种，红色线有4种填法，绿色框也被限制。那么答案就是： $2*1*1*4*4*2^{n-1}$
  - 意义： $前面同上，(4*4)表示f[n-3]所在直线的填法*红色线的填法$
  - 3、当f[n-3]前没有且f[n-3]也不相等时，f[n-3]所在直线只有1种填法，红色线有4种填法。因为绿色框没被限制，所以紫色线就有3种填法。答案就是： $2*1*1*4*3*2^{n-2}$
  - 意义： $说的很清楚了。$
现在，我们已经讨论完毕。
接下来我们看看当m>n时的情况：
- 当：（1,2）和（2,1）相等或是（3,1）（2,2）（1,3）相等时：
  - 可以画图发现：
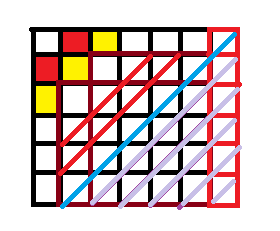
  - 我们对比上面的图可以发现灰色部分是紫色部分平移得到。
  - 那么多出来的蓝色线可以发现最上面一行与下面部分都是分成两个独立的。
  - 那么答案就是原答案X3
- 当：（2,2）（1,3）相等时
  - 我们可以发现，这个灰色线也是平移过来的，中间蓝线与上面的情况一样。
- 当：（3,1）（2,2）相等时
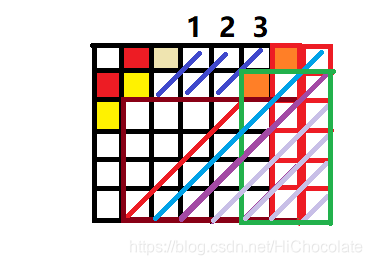
  - 这种情况要分类讨论。
  - 1、当f[n-3]所在斜线前有的话，那么绿色框中被控制，蓝色线自然只有3种填法，所以X3
  - 2、当f[n-3]前没有的话，当f[n-3]这里相等，那么绿色框依旧被控制，所以同上。
  - 3、当f[n-3]前没有且f[n-3]也不相等时，绿色框不被控制，这时我们就要讨论橙色部分相同或不相同了。
    - 一、当橙色部分相同时，红色线有3种填法，蓝色线有4种填法，而紫色线被控制，那么就有2种。答案 $3*4*2$
    - 二、当橙色部分不同时，红色线有1种填法，蓝色线有4种填法，而紫色线不被控制，有3种填法。答案 $1*4*3$
  - 然后，乘上别的没变的部分，再对比之前答案，惊奇地发现答案也是X3的。
经过即为繁琐的分类讨论后，我们就可以得到之后答案都是X3得到的。

讨论结束，我们得到答案——

                for i:=1 to n-4 do
                begin
                        f[i+1]:=(4*5+f[i]*4) mod mo;
                end;
                ans:=qsm(2,n)*(5*3+f[n-3]*2);
                op1:=(qsm(4,n-2)*qsm(2,n-1)*2*2) mod mo;
                op2:=(2*2*5*qsm(4,n-4)*qsm(2,n-1)) mod mo;
                if n=m then writeln((ans+op1+op2) mod mo)
                else
                begin
                        op21:=((f[n-3]*3+4*5)*qsm(2,n)) mod mo;
                        op22:=((f[n-3]*3+4*4)*qsm(2,n)) mod mo+(4*3*qsm(2,n-1)) mod mo;
                        writeln((((op1+op2)*3+op21+op22) mod mo*qsm(3,m-n-1)) mod mo);
                end;

当然如果还想更快，就可以把f用矩阵优化，时间做到O(log(n)+log(m))