LCA在线算法-基于ST表

LCA算法-ST在线算法

转自： https://blog.csdn.net/qq_35935435/article/details/54916022

这篇文章讲LCA算法（Least Common Ancestor)。

LCA:顾名思义，指在一棵有根树中，距离两个结点u和v最近的公共祖先（换句话说，是离根节点最远的公共祖先）。 
LCA算法：对于该问题，最容易想到的算法是分别从节点u和v回溯到根节点，获取u和v到根节点的路径P1，P2，其中P1和P2可以看成两条单链表，这就转换成常见问题：判断两个单链表是否相交，如果相交，给出相交的第一个点。该算法总的复杂度是O（n）（其中n是树节点个数）。但当数据量非常大且查询很频繁时，该算法无法在有效时间内查询出正解。所以本篇文章将介绍一种比较高效的算法解决该问题。在线算法（DFS+ST） 
①DFS 
举个例子。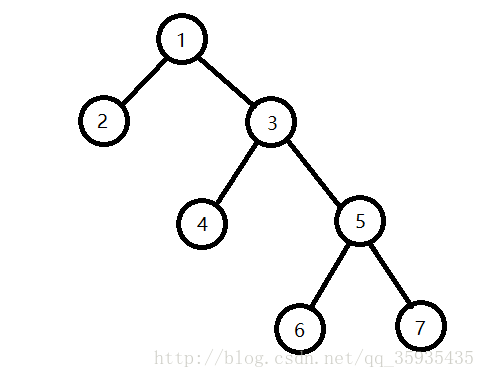 
 
假设遍历顺序从右至左，则DFS遍历可得。 
DFS遍历序列F_____________1 3 5 7 5 6 5 3 4 3 1 2 
深度序列deep______________1 2 3 4 3 4 3 2 3 2 1 2 
结点首次出现位置first ____1 12 2 9 3 6 4 
对于查询两个结点的LCA就是各自首次出现位置间深度最小的结点。于是可以转化为RMQ问题，在一段区间中寻找最小值。所以再用ST算法解决该问题。 
根据例题，如果询问LCA(4,7)，就相当于RMQ(4,7)。first[4]=9，first[7]=4。在深度序列中区间(4,9)是4 3 4 3 2 3，而最近公共祖先的深度就是这段区间中最小的2。再将深度代入遍历序列得到LCA(4,7)=3。 
②ST 
令F[i,j]为从下标i开始，长度为2^j的元素的最小值。那么状态转移方程就是F[i,j]=min(F[i,j-1],F[i+2^(j-1),j-1])。这个式子在这里有详细解释哦！ 
③查询 
假如要查询[m,n]的最小值，那么先求出一个最大的k。使k满足2^k<=(n-m+1)。于是我们可以将[m,n]分成两个（部分重叠的）长度为2^k的区间:[m,m+2^k-1],[n-2^k+1,n];F[m,k]为F[m,m+2^k-1]的最小值，F[n-2^k+1,k]是[n-2^k+1,n]的最小值。状态转移方程：RMQ(i,j)=min(F[m,k],F[n-2^k+1,k]); 
接下来看一下例题&代码。

LZOI2225 最近公共祖先

题目描述 
如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。 
输入 
第一行包含三个正整数n, q, s，分别表示树的结点个数、询问的个数和树根结点的序号。 
接下来n - 1行每行包含两个正整数u, v，表示u结点和v结点只见有一条直接连接的边（数据保证可以构成树）。 
接下来q行每行包含两个正整数a、b，表示询问a结点和b结点的最近公共祖先。 
输出 
输出包含q行，每行包含一个正整数，依次为每一个询问的结果。

CODE: 

#include<bits/stdc++.h>
using namespace std;
int n, q, root, u, v, a, b, F[50001], f[50001][21], first[50001], deep[50001], head[50001], tot;
bool vis[50001];
struct EDG
{
	int u, v, next;
}edg[10000];
void DFS(int u, int dep)
{
	vis[u] = 1;
	F[++tot] = u;
	first[u] = tot;
	deep[tot] = dep;
	for (int i = head[u]; i != 0; i = edg[i].next)
		if (!vis[edg[i].v])
		{
			DFS(edg[i].v, dep + 1);
			F[++tot] = u;
			deep[tot] = dep;
		}
}

int RQ(int i, int j)
{
	return deep[i] <= deep[j] ? i : j;
}
void ST(int N) {
	int temp = (int)(log((double)N) / log(2.0));
	for (int i = 0; i < N; i++) f[0][i] = i;
	for (int i = 1; i <= temp; ++i)
		for (int j = 0; j + (1 << i) - 2 < N; ++j)
			f[i][j] = RQ(f[i - 1][j], f[i - 1][j + (1 << (i - 1))]);
}
int query(int L, int R)
{
	int k = (int)(log((double)(R - L + 1)) / log(2.0));
	return RQ(f[k][L], f[k][R - (1 << k) + 1]);
}


int LCA(int u, int v)
{
	int x = first[u], y = first[v];
	if (x > y)swap(x, y);
	int res = query(x, y);
	return F[res];
}
int main()
{
	cin >> n >> q >> root;
	for (int i = 2; i <2*n; )
	{
		cin >> u >> v;
		edg[i] = EDG{ u,v,head[u] };
		head[u] = i++;
		edg[i] = EDG{ v,u,head[v] };
		head[v] = i++;
	}
	DFS(root, 1);
	ST(tot);
	for (int i = 1; i <= q; i++)
	{
		cin >> a >> b;
		cout << LCA(a, b) << endl;
	}
	return 0;
}