吴恩达机器学习笔记及作业代码实现中文版

第一个编程作业：单变量线性回归（python代码实现）

一元线性回归

问题描述
- 在本练习的这一部分中，您将使用只有单变量的线性回归方法预测餐车的利润。
- 假设你是一家连锁餐厅的首席执行官，正在考虑在不同的城市开设一家新店。
- 这家连锁公司已经在不同的城市拥有餐车，你也有这些城市的利润和人口数据。
- 您希望使用这些数据来帮助您选择要扩展到下一个城市。
- 文件ex1data1.txt包含线性回归问题的数据集。
- 第一列是一个城市的人口，第二列是该城市一辆餐车的利润。
- 利润的负值表示亏损。
绘制数据
- 在开始任何任务之前，通过可视化来理解数据通常是有用的。
- 对于这个数据集，您可以使用散点图来可视化数据，因为它只有两个属性需要绘制(利润和总体)。
- 你在现实生活中遇到的许多其他问题是多维的，不能在二维图上画出来。
- 首先，我们导入三个python库：numpy，pandas，matplotlib：
```
import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt 
```
- 然后我们使用pandas的read_csv函数读入文件ex1data1.txt，并打印出结果：
```
path = 'ex1data1.txt'
data = pd.read_csv(path, header = None, names = ['Population', 'Profit'])
data.head()
print(data) 
```
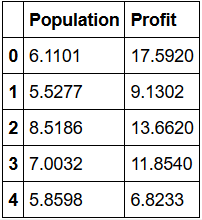
- 结果如下表所示，仅展示前五行内容：
- 接着我们给上表增加描述，得到一张新的表，表的内容已全部展示：
```
data1 = data.describe()
print(data1)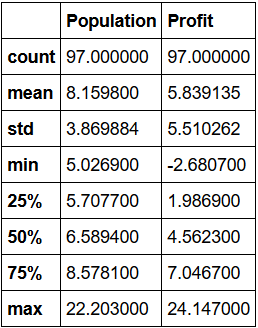
```
- 最后用plot方法得到训练数据散点图：
```
data.plot(kind = 'scatter', x = 'Population', y = 'Profit', figsize = (12, 8))
plt.show()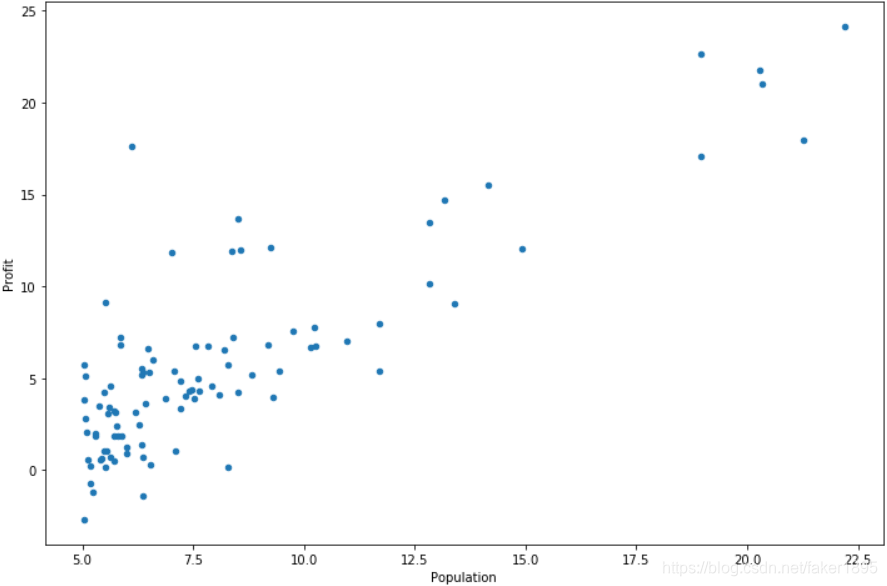
```
梯度下降法
- 现在让我们使用梯度下降来实现线性回归，以最小化成本函数。
- 首先，我们将创建一个以参数θ为特征函数的代价函数：
  - $J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}} \right)}^{2}}}$ 。
  - 其中： ${{h_\theta }}\left( x \right)={\theta^T}X={\theta _0}{x_0}+{\theta _1}{x_1}+{\theta_2}{x_2}+...+{\theta _n}{x_n}$ 。
```
def computeCost(X, y, theta):
    inner = np.power(((X * theta.T)) - y, 2)
    return np.sum(inner) / (2 * len(X))
```
- 让我们在训练集中添加一列，以便我们可以使用向量化的解决方案来计算代价和梯度。
```
data.insert(0, 'ones', 1)
```
- 现在我们来做一些变量初始化。
```
cols = data.shape[1]
X = data.iloc[:, 0:cols-1]
y = data.iloc[:, cols-1:cols]
```
- 观察下 X (训练集) and y (目标变量)是否正确。
```
print(X.head())
print(y.head())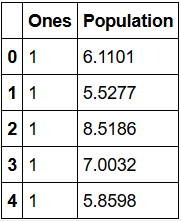
```
- 代价函数应该是numpy矩阵，所以我们需要转换X和Y，然后才能使用它们，所以我们还需要初始化theta。
```
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0, 0]))
print(theta)
```
- 此时theta已经是一个(1,2)矩阵[[0, 0]]，看下维度：
```
print(X.shape, theta.shape, y.shape)
```
- 得到三个矩阵维度分别为：((97, 2), (1, 2), (97, 1))。
- 计算代价函数 (theta初始值为0)：
```
result = computeCost(X, y, theta)
print(result)
```
- 得到结果为：32.0727338775。

批量梯度下降

确认梯度下降的一个好方法是观察J(θ)，然后检查其值是否随每一步计算而减少。假设您已经实现梯度下降法和computeCost正确，你的J(θ)不应该增加，而是应该收敛于一个稳定值的算法。

先给出公式： $\theta_j=\theta_j-\alpha*\frac{\partial J(\theta_0, \theta_1, ..., \theta_n)}{\partial \theta_j}$ 。

def gradientDescent(X, y, theta, alpha, iters):
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.ravel().shape[1])
    cost = np.zeros(iters)

    for i in range(iters):
        error = (X * theta.T) - y

        for j in range(parameters):
            term = np.multiply(error, X[:, j])
            temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))
        
        theta = temp
        cost[i] = computeCost(X, y, theta)

    return theta, cost

初始化一些附加变量：学习速率α和要执行的迭代次数。
```
alpha = 0.01
iters = 1000
```
现在让我们运行梯度下降算法来将我们的参数θ适合于训练集。
```
g, cost = gradientDescent(X, y, theta, alpha, iters)
print(g)
```
得到了一个g的矩阵：[[-3.24140214 1.1272942 ]]。
最后，我们可以使用我们拟合的参数计算训练模型的代价函数（误差）。
```
result1 = computeCost(X, y, g)
print(result1)
```
得到最后的代价值为：4.51595550308。

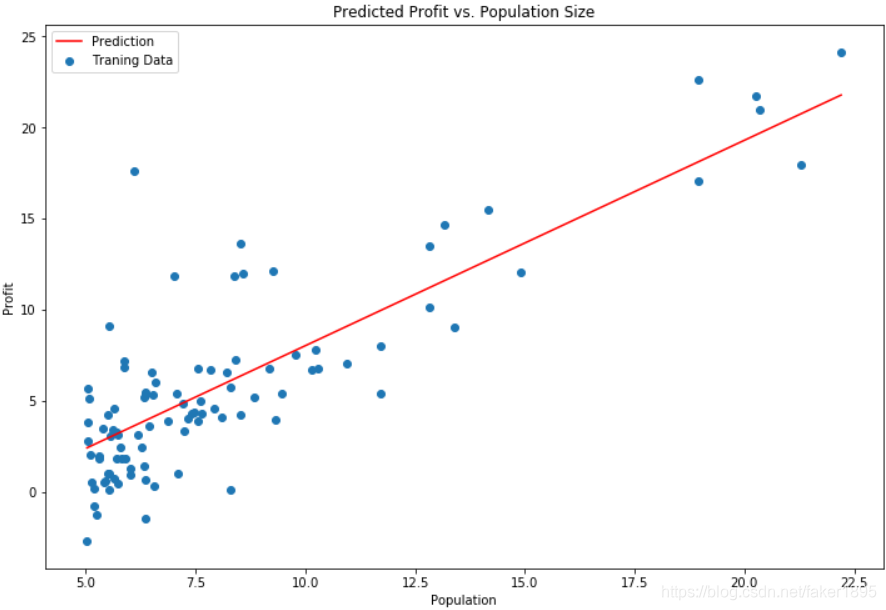
现在我们来绘制线性模型以及数据，直观地看出它的拟合。

x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + (g[0, 1] * x)

fig, ax = plt.subplots(figsize = (12, 8))
ax.plot(x, f, 'r', label = 'Prediction')
ax.scatter(data.Population, data.Profit, label = 'Traning Data')
ax.legend(loc = 2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

结果如下图所示：
由于梯度方程式函数也在每个训练迭代中输出一个代价的向量，所以我们也可以绘制。请注意，代价总是降低说明这是凸优化问题的一个例子。
```
fig, ax = plt.subplots(figsize = (12,8))
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()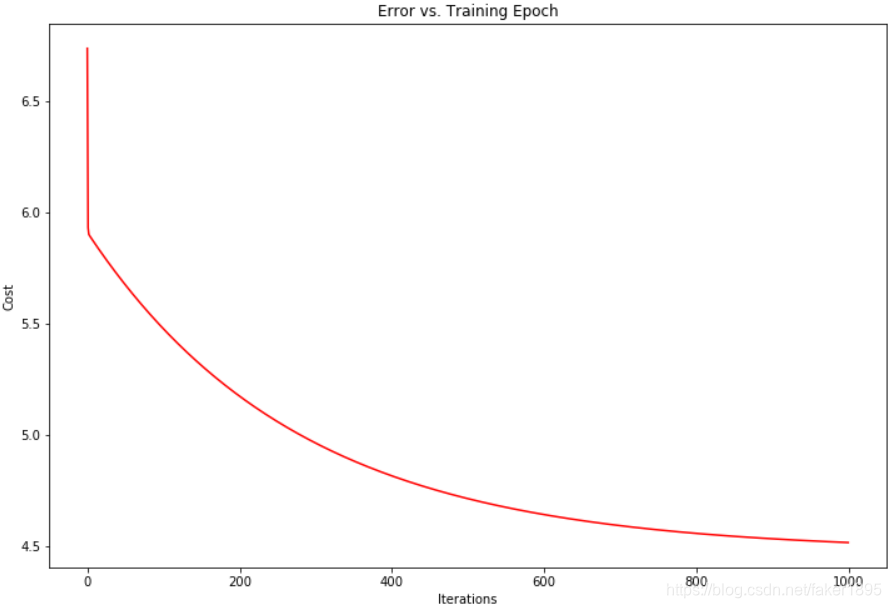
```

算法工程师修仙之路：吴恩达机器学习作业（一）

吴恩达机器学习笔记及作业代码实现中文版

第一个编程作业：单变量线性回归（python代码实现）

一元线性回归

猜你喜欢