算法工程师修仙之路：吴恩达机器学习（四）

吴恩达机器学习笔记及作业代码实现中文版

第四章 Logistic回归

---

分类

• 在分类问题中，要预测的变量y是离散的值，逻辑回归 (Logistic Regression) 算法是目前最流行使用最广泛的一种学习算法。

• 在分类问题中，我们尝试预测的是结果是否属于某一个类

  • 正确或错误。
  • 判断一封电子邮件是否是垃圾邮件。
  • 判断一次金融交易是否是欺诈。
  • 区别一个肿瘤是恶性的还是良性的。

• 我们将因变量(dependent variable)可能属于的两个类分别称为负向类（negative class）和正向类（ positive class），则因变量 y只取0或1，其中 0 表示负向类，1 表示正向类。

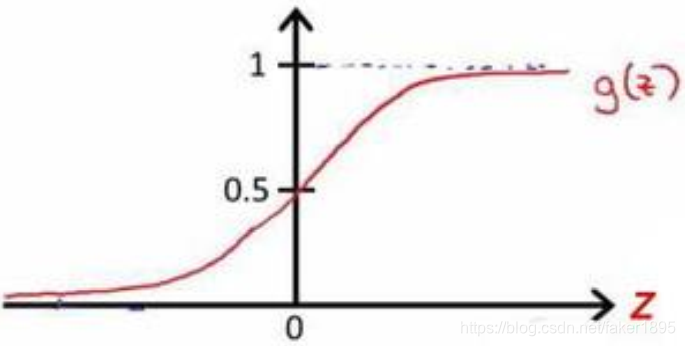
假设陈述

• 根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出 0 或 1，我们可以预测：

  • 当 $ℎ_\theta(x) >= 0.5$时，预测y=1。
  • 当 $ℎ_\theta(x) < 0.5$时，预测y=0。

• 逻辑回归模型的假设是： $ℎ_\theta(x) = g(\theta^TX)$。

  • 逻辑回归模型的输出变量范围始终在 0 和 1 之间。
  • X代表特征向量。
  • g代表逻辑函数（logistic function)。
  • 一个常用的逻辑函数为 S 形函数（Sigmoid function）。
  • 公式为 $g(z)=\frac{1}{1+e^{-z}}$。

    import numpy as np
    def sigmoid(z):
        return 1 / (1 + np.exp(-z))
    

  • $ℎ_\theta(x)$的作用是，对于给定的输入变量，根据选择的参数计算输出变量为1的可能性（estimated probablity）即 $ℎ_\theta(x) = P(y=1|x; \theta)。$

决策界限

• 在逻辑回归中，我们预测：

  • 当 $ℎ_\theta(x) >= 0.5$时，预测y=1。
  • 当 $ℎ_\theta(x) < 0.5$时，预测y=0。
    

• 根据S 形函数图像，我们知道：

  • 当z=0时，g(z)=0.5。
  • 当z>0时，g(z)>0.5。
  • 当z<0时，g(z)<0.5。

• $z=\theta^Tx$，即：

  • 当 $z=\theta^Tx&gt;= 0$时，预测y=1。
  • 当 $z=\theta^Tx&lt; 0$时，预测y=0。

• 我们可以用非常复杂的模型来适应非常复杂形状的判定边界。

代价函数

• 对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将 $h_\theta(x)=\frac{1}{1+e^{-\theta^T(x)}}$带入到这样定义了的代价函数中时，我们得到的代价函数将是一个非凸函数（ non-convexfunction）。这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。

• 我们重新定义逻辑回归的代价函数为：

  • $J(\theta_0, \theta_1, ..., \theta_n)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)}), y^{(i)})$
  • $Cost(h_\theta(x^{(i)}), y^{(i)})=−y^{(i)}log(h_\theta(x^{(i)})) − (1 − y^{(i)}) log(1-h_\theta(x^{(i)}))$。

• 这样构建的函数的特点是：

  • 当实际的y=1且 $h_\theta(x)$也为1时误差为 0。

  • 当y=1但 $h_\theta(x)$不为 1 时误差随着 $h_\theta(x)$变小而变大。

  • 当实际的y=0且 $h_\theta(x)$也为 0 时代价为 0。

  • 当y=0但 $h_\theta(x)$不为 0 时误差随着 $h_\theta(x)$的变大而变大。

  • 代价函数 $J(\theta)$会是一个凸函数，并且没有局部最优值。

    import numpy as np
    def cost(theta, X, y):
        theta = np.matrix(theta)
        X = np.matrix(X)
        y = np.matrix(y)
        first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
        second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
        return np.sum(first - second) / (len(X))
    

• 在得到这样一个代价函数以后，我们便可以用梯度下降算法来求得能使代价函数最小的参数了。

• 逻辑回归的梯度下降算法推导：

  • $J(\theta_0, \theta_1, ..., \theta_n)=-\frac{1}{m}\sum_{i=1}^m[y^{(i)}log(h_\theta(x^{(i)})) + (1−y^{(i)}) log(1-h_\theta(x^{(i)}))]$ 。
  • 考虑： $h_\theta(x^{(i)})=\frac{1}{1+e^{-\theta^Tx^{(i)}}}$。
  • 则： $y^{(i)}log(h_\theta(x^{(i)})) + (1−y^{(i)}) log(1-h_\theta(x^{(i)}))=y^{(i)}log(\frac{1}{1+e^{-\theta^Tx^{(i)}}})+(1−y^{(i)})log(1-\frac{1}{1+e^{-\theta^Tx^{(i)}}})=-y^{(i)}log({1+e^{-\theta^Tx^{(i)}}})-(1−y^{(i)})log({1+e^{\theta^Tx^{(i)}}})$。
  • 所以： $\frac{\partial J(\theta)}{\partial \theta_j}=\frac{\partial [-\frac{1}{m}\sum_{i=1}^m[-y^{(i)}log({1+e^{-\theta^Tx^{(i)}}})-(1−y^{(i)})log({1+e^{\theta^Tx^{(i)}}})]]}{\partial \theta_j}={-\frac{1}{m}\sum_{i=1}^m[-y^{(i)}(\frac{-x_j^{(i)}e^{-\theta^Tx^{(i)}}}{1+e^{-\theta^Tx^{(i)}}})-(1−y^{(i)})\frac{x_j^{(i)}e^{\theta^Tx^{(i)}}}{1+e^{\theta^Tx^{(i)}}}]}={-\frac{1}{m}\sum_{i=1}^m[y^{(i)}(\frac{x_j^{(i)}}{1+e^{\theta^Tx^{(i)}}})-(1−y^{(i)})\frac{x_j^{(i)}e^{\theta^Tx^{(i)}}}{1+e^{\theta^Tx^{(i)}}}}]={-\frac{1}{m}\sum_{i=1}^m}[\frac{y^{(i)}x_j^{(i)}-x_j^{(i)}e^{\theta^Tx^{(i)}}+y^{(i)}x_j^{(i)}e^{\theta^Tx^{(i)}}}{1+e^{\theta^Tx^{(i)}}}]={-\frac{1}{m}\sum_{i=1}^m}[\frac{x_j^{(i)}[y^{(i)}{(1+e^{\theta^Tx^{(i)}})}-e^{\theta^Tx^{(i)}}]}{1+e^{\theta^Tx^{(i)}}}]={-\frac{1}{m}\sum_{i=1}^m}(y^{(i)}-\frac{e^{\theta^Tx^{(i)}}}{1+e^{\theta^Tx^{(i)}}})x_j^{(i)}={-\frac{1}{m}\sum_{i=1}^m}(y^{(i)}-\frac{1}{1+e^{-\theta^Tx^{(i)}}})x_j^{(i)}={-\frac{1}{m}\sum_{i=1}^m}[y^{(i)}-h_\theta({x^{(i)}})]x_j^{(i)}={\frac{1}{m}\sum_{i=1}^m}[h_\theta({x^{(i)}})-y^{(i)}]x_j^{(i)}$。

• 虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样，但是这里的 $ℎ_\theta(x)=g(\theta^TX)$与线性回归中不同，所以实际上是不一样的。另外，在运行梯度下降算法之前，进行特征缩放依旧是非常必要的。