之前说过,基于NLP处理的算法思想目前主要有两大流派:统计论流派和深度学习流派。而在统计论中,常用的 4 大概率模型分别是 朴素贝叶斯模型,隐马尔科夫模型,最大熵模型和条件随机场模型。
对于朴素贝叶斯模型,前面已经多次打过交道,原理也相对简单。这里解析第二大模型 -- 隐马尔科夫模型。我要说明的是,任何理论,都是以基本数学原理为思想,但是每个人的想法不同,解析的角度不同,求解的思路不同,所以我的角度未必是正式的书面表达角度,但数学思想殊途同归。
首先介绍几个熵的概念以及它们的联系:
信息熵:衡量信息量的大小
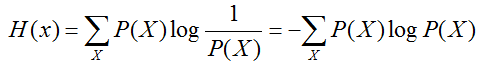
通常以 2 为底,单位 bit
互信息:衡量 X 、Y 的信息不确定消除性,说白了就是 X、Y的信息互相包含性,越少说明越独立
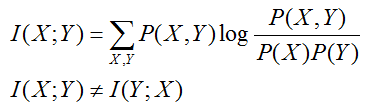
可以看到,如果 X,Y 独立,则 I(X;Y) = 0
联合熵和条件熵:联合概率分布信息量和条件概率分布信息量的衡量
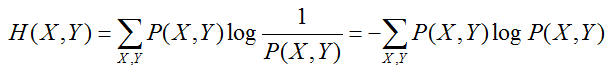
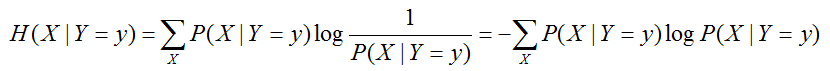
互信息和联合熵、条件熵之间的联系
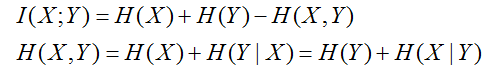
交叉熵和 KL散度

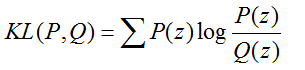
还记得交叉熵在深度学习中经常用来作为分类问题的损失函数,但从公式可以看出,当P(z) = Q(z) 时,交叉熵的值是 Q(z)的信息熵,而在 one-hot 编码的分类情况下,Q(z) 的信息熵为0 。 因此交叉熵只适合单分类模型,多分类模型 KL 散度可能更适合(个人根据公式推测)。
现在是时候回到重点:隐马尔科夫模型了
一个马尔科夫模型 HMM 由以下组成
(1)隐状态:系统的真实状态序列,有一个马尔科夫过程描述。 -- 说白了就是概率状态序列
(2)状态转移概率矩阵:状态之间转换概率 -- Viterbi 算法就是这个过程的简化(用最大值)
(3)π 向量:隐状态的初始概率。
(4)发射概率矩阵。-- 表达各个显性因子对隐状态的影响概率矩阵。
个人觉得隐马尔科夫模型有点时序的味道,类似 RNN 模型。书面的表达太过于正式并且长篇大论难以快速理解。我觉得可以这么说:
(1)首先给定一个 π 向量 表达初始概率,比如假如我知道一年中有八成的概率下雨,那么我预测今天下雨的概率初始值为
π = [0.8 0.2] ,这就是 π 向量:隐状态的初始概率。
(2)现在问题又来了,我还知道如果下雨,第二天九成概率也是下雨,如果不下雨,那么九成也不下雨。这就是转移概率矩阵
stateP = [[0.9 0.1],[0.1 0.9]] ,那么我们就要用当前状态也就是隐状态乘以转移概率矩阵以获得新的状态概率。
下雨概率 0.8 * 0.9 + 0.2 * 0.1 = 0.74
不下雨概率 0.8 * 0.1 + 0.2 * 0.9 = 0.26
即 [0.74 0.26] = π * stateP.T (表示转置)
注意,在维特比算法中,我们不需要由转移概率矩阵的全概率公式,而仅仅只需要最大概率值,也就是
下雨概率 max(0.8 * 0.9,0.2 * 0.1) = 0.72
不下雨概率 max(0.8 * 0.1 , 0.2 * 0.9) = 0.18
(3)以上只是隐状态的转移,但是还有显式观察值,今天的湿度为潮湿,那如果潮湿的情况下下雨的概率为八成,则发射矩阵为 [0.8 0.2] 也就是 [0.74 0.26] × [0.8 0.2] = [0.592 0.052] 这就是今天的状态。
以此类推,往后 n 天的状态可由状态转移概率矩阵和发射矩阵形成的马尔科夫过程构成的隐状态表达。
相应的代码如下:
# -*- coding:utf-8 -*-
# 隐马尔科夫模型
from numpy import *
# 起始概率
startP = mat([0.63,0.17,0.20])
# 转移概率矩阵
stateP = mat([[0.5,0.25,0.25],[0.375,0.125,0.375],[0.125,0.625,0.375]])
# 发射概率矩阵
emitP = mat([[0.6,0.25,0.05],[0.20,0.25,0.1],[0.05,0.25,0.50]])
# 计算第一次转移
state1Emit = multiply(startP , emitP[0,:])
print state1Emit
# 计算第二次转移
state2Emit = state1Emit * stateP.T
state2Emit = multiply(state2Emit,emitP[1,:])
print state2Emit
# 计算第三次转移
state3Emit = state2Emit * stateP.T
state3Emit = multiply(state3Emit,emitP[2,:])
print state3Emit
# 维特比算法:状态转移矩阵只需要最大值,而不需要计算全部值相加
def viterbi():
startP = [0.63,0.17,0.20]
emitP = [[0.6,0.25,0.05],[0.20,0.25,0.1],[0.05,0.25,0.50]]
# 计算第一次转移,这点不变
state1Emit = multiply(startP,emitP[0])
stateP = [[0.5,0.25,0.25],[0.375,0.125,0.375],[0.125,0.625,0.375]]
# 计算转移概率时,只需要保留最大转移概率值
v = []
for y in stateP:
v.append(float(max(multiply(state1Emit,y))))
state2Emit = multiply(v,emitP[1])
print state2Emit
# 计算第三次转移,同样只在转移概率计算时修改成最大值
v = []
for y in stateP:
v.append(float(max(multiply(state2Emit,y))))
state3Emit = multiply(v,emitP[2])
print state3Emit
viterbi()