从实际和理论的角度联系的理解一阶sigma-delta

版权声明：小兵所有 https://blog.csdn.net/weixin_42767056/article/details/84403480

1 标准画法（传输函数方法）

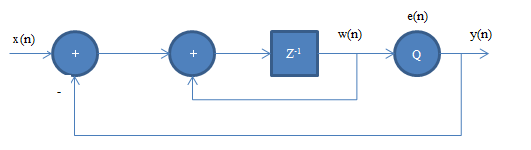
用传输函数方法：

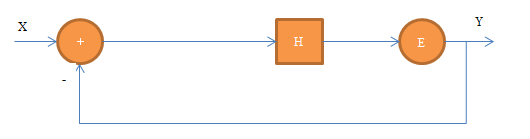
可以导出来：

中间：H = 1 / (z - 1)
整体：Y = (X - Y) * H + E
代入整理就有下式
y(n) = x(n-1) + e(n) - e(n-1)

但是不直观有木有，发现最终是在图的画法上

2.1 改动画法（直观分析）

将图改动下，把加减变量线合起来如下图

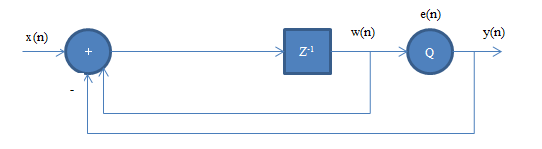
w(n) = {x(n) - [w(n) + e(n)] + w(n)} [延一拍]  
     = [x(n) - e(n)] [延一拍]
     = x(n-1) - e(n-1)
y(n) = w(n) + e(n)
     = x(n-1) - e(n-1) + e(n) 

这才是差分再求和的理念嘛

2.2 实际与理论相关联

1、实际

x，w，e，y 均为模拟表示
假设x(n)恒为0.7，y(n)可取±1，w(n-1) = 0.1

n-1级 积分器结果：w(n-1) > 0
n-1级 量化器结果：y(n-1)取1
n  级 积分增量  ：δ(n-1) = x(n-1) - y(n-1) = 0.7 - 1 = -0.3
n  级 积分器结果：w(n) = w(n-1) + x(n-1) - y(n-1) = 0.1 -0.3 = -0.2 < 0 
n  级 量化器结果：y(n)取-1

n-1级 量化误差  ：e(n-1) = y(n-1) - w(n-1) =  1 - 0.1    =  0.9
n  级 量化误差  ：e(n)   = y(n)   - w(n)   = -1 - (-0.2) = -0.8

2、套用理论

y(n) = x(n-1) - e(n-1) + e(n) = 0.7 - 0.9 + (-0.8) = -1

终于把实际和理论对上了

3、变形

实际电路的积分中，积分进去的量总是成一定比例k的，可以等效整个通路都乘以k。